Cite this Article
Saha Ray S. New analytical exact solutions of time fractional KdV–KZK equation by Kudryashov methods. Chinese Physics B, 2016, 25(4): 040204  
Permissions
New analytical exact solutions of time fractional KdV–KZK equation by Kudryashov methods
Saha Ray S†,
National Institute of Technology, Department of Mathematics, Rourkela-769008, India

 

† Corresponding author. E-mail: santanusaharay@yahoo.com

Abstract
Abstract

In this paper, new exact solutions of the time fractional KdV–Khokhlov–Zabolotskaya–Kuznetsov (KdV–KZK) equation are obtained by the classical Kudryashov method and modified Kudryashov method respectively. For this purpose, the modified Riemann–Liouville derivative is used to convert the nonlinear time fractional KdV–KZK equation into the nonlinear ordinary differential equation. In the present analysis, the classical Kudryashov method and modified Kudryashov method are both used successively to compute the analytical solutions of the time fractional KdV–KZK equation. As a result, new exact solutions involving the symmetrical Fibonacci function, hyperbolic function and exponential function are obtained for the first time. The methods under consideration are reliable and efficient, and can be used as an alternative to establish new exact solutions of different types of fractional differential equations arising from mathematical physics. The obtained results are exhibited graphically in order to demonstrate the efficiencies and applicabilities of these proposed methods of solving the nonlinear time fractional KdV–KZK equation.

PACS: 02.70.−c;
Keyword:KdV–Khokhlov–Zabolotskaya–Kuznetsov equation;Kudryashov method;modified Kudryashov method;fractional complex transform;modified Riemann–Liouville derivative;
1. Introduction

In recent years, fractional calculus has played a very important role in various application areas, such as modeling anomalous diffusion, heat transfer, seismic wave analysis, signal processing, control theory, image processing, and many other fractional dynamical systems.[1–6] Fractional differential equations (FDEs) are the generalized form of classical differential equations of integer order. The FDEs are inherently multi-disciplinary with their application across diverse disciplines of applied science and engineering. Recently, FDEs have attracted great attention due to their applications in various real physical problems. The properties of several physical phenomena are found to be best described by FDEs. For this purpose, a reliable and efficient technique is essential for solving the nonlinear FDEs. In this connection, it is worthwhile to mention the recent notable studies of the solutions of FDEs, integral equations and fractional partial differential equations (FPDEs) of physical interest. Several analytical and numerical methods have been employed to develop approximate and exact solutions of FDEs.[7–18]

The sound propagation in fluid is determined by nonlinearity, diffraction, absorption and dispersion. For modelling the nonlinear sound propagation in fluid, the combined effects of nonlinearity, absorption, dispersion and diffraction should be taken into account. The description of sound propagation in fluid requires accurate representations of nonlinearity, dispersion, absorption, and diffraction. The KdV–Khokhlov–Zabolotskaya–Kuznetsov (KdV–KZK) equation describes all the basic physical mechanisms of sound propagation in fluids.[19]

Now we consider the (3+1)-dimensional time fractional KdV–KZK equation:

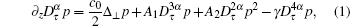
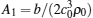
where 0 < α ≤ 1, , and with ɛ being the parameter of nonlinearity, b is the diffusivity parameter, ρ0 is the ambient fluid density, p is the acoustic pressure, τ = t − z/c0 is the retarded time variable with z being the direction of sound propagation, c0 being the small signal speed of sound, and γ is the adiabatic index defined as γ = cp/cv, with cp and cv being the specific heats at constant pressure and constant volume.

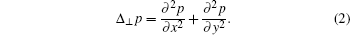
The first term on the right-hand side of Eq. (1) represents diffraction. The second term refers to thermoviscous attenuation as in Burgers’ equation, and the third term describes the nonlinearity. In comparison to KdV-Burgers equation, the KdV–KZK equation has only one extra term. The diffusivity parameter b is defined as b = ζ + 4η/3, where ζ and η are the bulk and shear viscosity. The transverse Laplacian can be written in Cartesian coordinates as

The KdV–KZK equation is an augmented form of KdV–Burgers equation. In addition to absorption, dispersion and nonlinearity, it also includes the diffraction. The nonlinear parabolic KdV–KZK equation describes the combined effects of diffraction, absorption, dispersion and nonlinearity.

The KdV–KZK equation for fluids has profound applications in aerodynamics and acoustics, and also its extension to solids has applications in biomedical engineering and in nonlinear acoustical nondestructive testing.

Nonlinear FDEs can be transformed into integer-order nonlinear ordinary differential equations via fractional complex transform with the help of the modified Riemann–Liouville fractional derivative and corresponding useful formulae. The present methods[20–25] under study can be devised to develop the exact analytical solutions for the time fractional KdV–KZK equation. The main motivation of this paper is to develop the exact solutions of the fractional order KdV–KZK equation. To the best of the author’s knowledge, the exact analytical solutions for the fractional KdV–KZK equation have been reported for the first time in this paper.

The rest of this paper is organized as follows. In Section 2, some definitions and corresponding properties of the modified Riemann–Liouville derivative are described. In Section 3, the description of the algorithm for solving FPDEs by using both the classical Kudryashov method and modified Kudryashov method via fractional complex transform is presented. Then in Section 4, these methods have been implemented to establish new exact solutions for the time fractional KdV–KZK equation. Next, in Section 5, the numerical simulations for the nonlinear time fractional KdV–KZK equation are discussed. In Section 6, some conclusions are drawn from the present studies.

2. Description of modified Riemann–Liouville derivative and some properties

The modified Riemann–Liouville derivative[26–29] of order α is given as follows:

which can be written as

Some properties for the modified Riemann–Liouville derivative given in Refs. [26]–[29] are as follows:

which are the direct consequences of the following equality:

which holds for a non-differentiable function. It is noted that from Eqs. (6) and (7), the function f (h) is differentiable in Eq. (6) but non-differentiable in Eq. (7).

3. Algorithm of the method applied with fractional complex transform

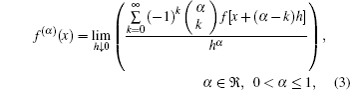
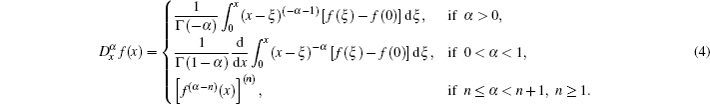
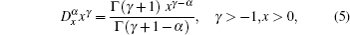
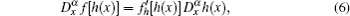
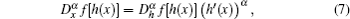
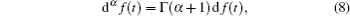
In this section, an algorithm is presented for the analytical solutions of Eq. (1) by using both the classical Kudryashov method and modified Kudryashov method.[20,23,24] The main steps of this method are described as follows.

Step 1 Suppose that a nonlinear FPDE, say, in four independent variables x, y, z, and t is given by

where , , and are modified Riemann–Liouville derivatives of u, where u = u(x,y,z,t) is an unknown function, P is a polynomial in u and contains its various partial derivatives including the highest order derivatives and nonlinear terms.

Step 2 By using the fractional complex transform:[30,31]

where l, m, k, and λ are constants.

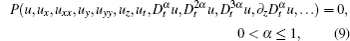
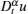
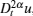
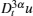
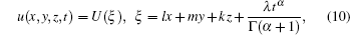
By using the chain rule, we have

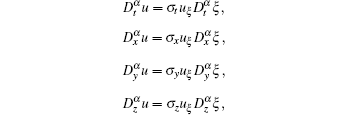
where σt, σx, σy, and σz are the fractal indexes,[32,33] without loss of generality we can take σt = σx = σy = σz = κ, where κ is a constant.

Thus, the FPDE (9) is reduced to the following nonlinear ordinary differential equation (ODE) for u(x,y,z,t) = U(ξ):

Step 3 We assume that the exact solution of Eq. (11) can be expressed in the following form:

where ai (i = 0,1,2,…,N) are constants to be determined later, such that aN ≠ 0, while Q(ξ) has the following form:

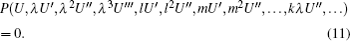
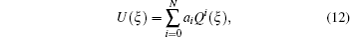
for the classical Kudryashov method

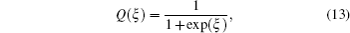
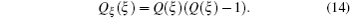
which satisfies the first order differential equation

for the modified Kudryashov method

This function satisfies the first order differential equation

Step 4 To determine the dominant term with the highest order of singularity, we substitute

into all terms of Eq. (11). Then the degrees of all terms of Eq. (11) are compared and consequently two or more terms with the lowest degree are chosen. The maximum value of p is the pole of Eq. (11) and it is equal to N. This method can be employed when N is integer. If N is noninteger, the equation under study needs to be transformed and then the above procedure is to be repeated.

Step 5 The necessary number of derivatives of function U(ξ) with respect to ξ can be calculated by using the computer algebra systems of any mathematical software.

Step 6 Substituting the derivatives of function U(ξ) along with Eqs. (12) into Eq. (11) in the case of the classical Kudryashov method or substituting the derivatives of function U(ξ) along with Eq. (12) into Eq. (11) in the case of the modified Kudryashov method, equation (11) becomes the following form:

where Φ [Q(ξ)] is a polynomial in Q(ξ). Then collecting all terms with the same powers of Q(ξ) and equating each coefficient of this polynomial to zero yields a set of algebraic equations for ai (i = 0,1,2,…, N) and λ.

Step 7 Solving the algebraic equation system obtained in Step 6 and subsequently substituting these values of the constants ai (i = 0,1,2,…, N) and λ into the resulting equation system, we can obtain the explicit exact solutions of Eq. (1) instantly. The obtained solutions may involve the symmetrical hyperbolic Fibonacci functions.[34,35] The symmetrical Fibonacci sine, cosine, tangent and cotangent functions are respectively defined as follows:

4. Exact solution of time fractional KdV–KZK equation

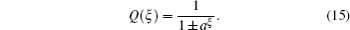
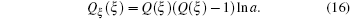
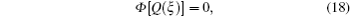
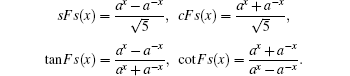
In the present section, the new exact analytical solutions of the time fractional KdV–KZK equation are obtained for the first time by using the Kudryashov method and modified Kudryashov method respectively.

4.1. Kudryashov method for time fractional KdV–KZK equation

In the present analysis, we introduce the following fractional complex transform into Eq. (1):

where k and λ are constants.

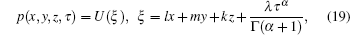
By applying the fractional complex transform (19), equation (1) can be transformed into the following nonlinear ODE:

Integrating Eq. (20) with respect to ξ once, we have

where C1 is the integration constant.

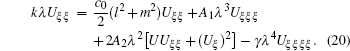
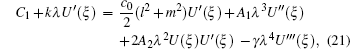
The dominant terms with the highest order of singularity are γ λ 4U‴(ξ) and 2A2 λ2U(ξ)U′(ξ). Thus the pole order of Eq. (21) is N = 2.

Therefore, the solution that we seek is in the following form:

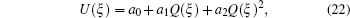
where a0, a1, and a2 are constants to be determined later.

Substituting the derivatives of function U(ξ) with respect to ξ and taking into account the ansatz (22) in Eq. (21), we obtain a system of algebraic equations in the following form:

Solving this system, we obtain the following family of solutions.

Case I

Substituting the above parameter values into the ansatz given by Eq. (22), we obtain the following solution of Eq. (1):

where ξ = lx + my + kz + λtα/[Γ (α +1)] and λ = − A1/(5γ).

Case II

Substituting the above parameter values into the ansatz given by Eq. (22), we obtain the following solution of Eq. (1):

where ξ = lx + my + kz + λtα/[Γ (α +1)] and λ = A1/(5γ).

4.2. Modified Kudryashov method for time fractional KdV–KZK equation

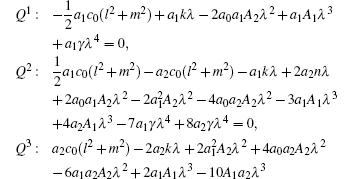
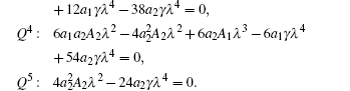
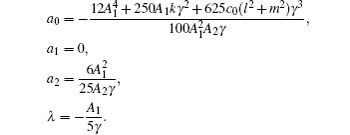
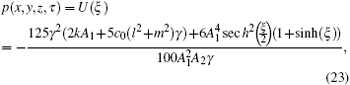
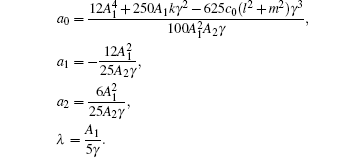
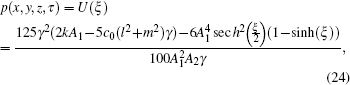
Following the same preceding argument, equation (21) is to be acquired. Then substituting the derivatives of function U(ξ) with respect to ξ into Eq. (21) and the ansatz given by Eq. (22) into the resulting Eq. (21), we obtain a system of algebraic equations in the following form:

Solving this system we obtain the family of solutions as follows:

Case I

Substituting the above parameter values into the ansatz given by Eq. (22), we obtain the following solutions of Eq. (1):

where ξ = lx + my + kz + λtα/(Γ (α +1)) and λ = −A1/(5γ lna).

Case II

Substituting the above parameter values into the ansatz given by Eq. (22), we obtain the following solutions of Eq. (1):

where ξ = lx + my + kz + λtα/(Γ (α +1)) and λ = A1/(5γ lna).

5. Numerical results and discussion

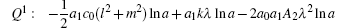
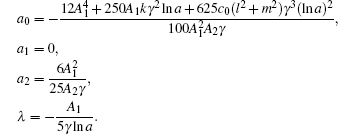
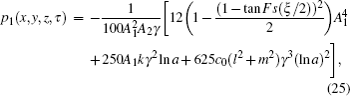
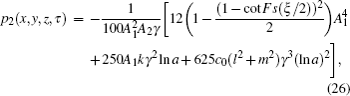
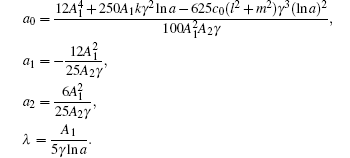
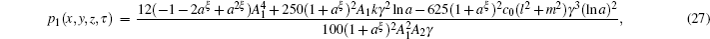
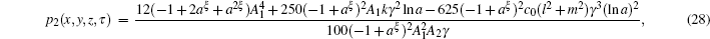
In this section, the numerical simulations of the time-fractional KdV–KZK equation are presented graphically. Here the exact solutions (23) and (24) obtained by the classical Kudryashov method and also the exact solutions (25)–(28) obtained by the modified Kudryashov method are used to draw the three-dimensional (3D) solution graphs.

5.1. Numerical simulations for the solutions obtained by the classical Kudryashov method

In the present analysis, equations (23) and (24) are used for drawing the solution graphs for the time-fractional KdV–KZK equation in the cases of fractional and classical orders.

Solitary wave solutions for Eq. (23) at A1 = 10, A2 = 20, γ = 0.5, k = l = m = 0.5, and c0 = 1, when (a) α = 0.5 and (b) α = 1.

Solitary wave solutions for Eq. (24) at A1 = 10, A2 = 20, γ = 0.5, k = l = m = 0.5, and c0 = 1, when (a) α = 0.5 and (b) α = 1.

5.2. Numerical simulations for the solutions obtained by the modified Kudryashov method

In the present analysis, equations (25)–(28) are used for drawing the solution graphs for the time-fractional KdV–KZK equation in the cases of fractional and classical orders.

In the present numerical simulations, the solitary wave solutions for Eqs. (23)–(28) are demonstrated in 3D graphs. From the above figures, it may be observed that the solution surfaces obtained by the classical Kudryashov method for Eq. (23) are anti-kink solitary waves. On the other hand, the solution surfaces obtained by the classical Kudryashov method for Eq. (24) show the kink solitary waves. Similarly, the solution surfaces obtained by the modified Kudryashov method for Eqs. (25) and (27) show the anti-kink and kink solitary waves respectively. However, in the case of the solution surfaces obtained by the modified Kudryashov method for Eqs. (26) and (28), single soliton solitary waves of different shapes are observed.

Solitary wave solutions for Eq. (25) at A1 = 10, A2 = 20, γ = 0.5, k = l = m = 0.5, c0 = 1, and a = 10 when (a) α = 0.25 and (b) α = 1.

Solitary wave solutions for Eq. (26) at A1 = 10, A2 = 20, γ = 0.5, k = l = m = 0.5, c0 = 1, and a = 10 when (a) α = 1 and (b) α = 0.5.

Solitary wave solutions for Eq. (27) at A1 = 10, A2 = 20, γ = 0.5, k = l = m = 0.5, c0 = 1, and a = 10 when (a) α = 0.25 and (b) α = 1.

Solitary wave solutions for Eq. (28) at A1 = A2 = γ = k = l = m = c0 = 1, and a = 10 when (a) α = 1 and (b) α = 0.75.

5.3. Physical significance for the solution of the KdV–KZK equation

The KdV–KZK equation covers all the four basic physical mechanisms of nonlinear acoustics, viz. diffraction, nonlinearity, dissipation and dispersion. The solution of the KdV–KZK equation describes a shock wave as a transition between two constant velocity values. This transition can undergo oscillations due to the dispersion.

The obtained results are related to physical phenomenon in Cantorian time-space. These results enrich the properties of the genuinely nonlinear phenomenon. To the best of the author’s knowledge, the obtained solutions in this paper have not been reported in the literature. The reported results have a potential application in observing the structure of the KdV–KZK equation from micro-physical to macro-physical behavior of substances in the real world.

6. Conclusions

In this paper, the new exact solutions of the time fractional KdV–KZK equation are obtained by the classical Kudryashov and modified Kudryashov method respectively with the help of the fractional complex transform. The fractional complex transform is employed in order to convert an FDE into its equivalent ODE form. So, the fractional complex transform facilitates solving FDEs. Two methods are successfully used to solve the nonlinear time fractional KdV–KZK equation. The new obtained exact solutions may be useful for explaining some physical phenomena accurately. The present analysis indicates that the methods discussed in this paper are effective and efficient for analytically solving the time fractional KdV–KZK equation. It also demonstrates that the performances of these methods are substantially influential and absolutely reliable for finding new exact solutions in terms of symmetrical hyperbolic Fibonacci function solutions. In the present analysis, the discussed methods clearly avoid linearization, discretization, and unrealistic assumptions and therefore these methods provide exact solutions efficiently and accurately. To the best of the author’s knowledge, new exact analytical solutions of the time fractional KdV–KZK equation are obtained for the first time in this respect.

Reference
1Podlubny I1999Fractional Differential Equations of Mathematics in Science and EngineeringNew YorkAcademic PressVol. 198
2Hilfer R2000Applications of Fractional Calculus in PhysicsSingaporeWorld Scientific
3Debnath LBhatta D2006Integral Transforms and Their ApplicationsBoca RatonChapman and Hall/CRC.
4Sabatier JAgrawal O PTenreiro Machado J A2007Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and EngineeringNetherlandsSpringer
5Ortigueira M D2011“Fractional Calculus for Scientists and Engineers”Lecture Notes in Electrical Engineering84NetherlandsSpringer
6Das S2011Functional Fractional CalculusNew YorkSpringer
7Diethelm KFord N JFreed A D 2002 Nonlinear Dynamics 29 3
8Liu FAnh VTurner I 2004 J. Comput. Appl. Math. 166 209
9Saha Ray S2007Phys. Scr.75article number 008 53
10Ortigueira M DTenreiro Machado J A 2006 Signal Processing 86 2503
11Saha Ray S 2008 Appl. Math. Comput. 202 544
12Tong BHe YWei LZhang X 2012 Phys. Lett. 376 2588
13Liu FZhuang PBurrage K 2012 Comput. Math. Appl. 64 2990
14Saha Ray S 2012 Appl. Math. Comput. 218 5239
15Kadem AKılıçman A 2012 Abstr. Appl. Anal. 2012 1
16Gupta A KSaha Ray S 2015 Appl. Math. Model. 39 5121
17Sahoo SSaha Ray S 2015 Physica A: Statistical Mechanics and Its Applications 434 240
18Saha Ray SSahoo S 2015 Comput. Math. Appl. 70 158
19Gan W S2007Acoustical Imaging28445
20Kudryashov N A 2009 Commun. Nonlinear Sci. Numer. Simul. 14 1891
21Ryabov P NSinelshchikov D IKochanov M B 2011 Appl. Math. Comput. 218 3965
22Kudryashov N A 2012 Commun. Nonlinear Sci. Numer. Simul. 17 2248
23Kabir M MKhajeh AAghdam E AKoma A Y2011Math. Methods Appl. Sci.34244
24Ege S MMisirli E 2014 Advances in Difference Equation 2014 135
25Taghizadeh NMirzazadeh MMahmoodirad A 2013 Indian J. Phys. 87 781
26Jumarie G 2005 Appl. Math. Lett. 18 739
27Jumarie G 2006 Comput. Math. Appl. 51 1367
28Jumarie G 2009 Appl. Math. Lett. 22 378
29Jumarie G2013Mathematics and Statistics150
30Su W HYang X JJafari HBaleanu D 2013 Advances in Difference Equations 2013 1
31Yang X JBaleanu DSrivastava H M2015Local Fractional Integral Transforms and Their ApplicationsLondonAcademic Press
32He J HElagan S KLi Z B 2012 Phys. Lett. 376 257
33Güner OBekir ACevikel A C 2015 Eur. Phys. J. Plus 130 146
34Stakhov ARozin B 2005 Chaos, Solitons, and Fractals 23 379
35Pandir Y 2014 Appl. Math. Inform. Sci. 8 2237