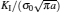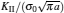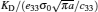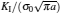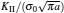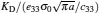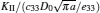Cite this Article
Chen Shen-Shen, Wang Juan, Li Qing-Hua. Two-dimensional fracture analysis of piezoelectric material based on the scaled boundary node method. Chinese Physics B, 2016, 25(4): 040203  
Permissions
Two-dimensional fracture analysis of piezoelectric material based on the scaled boundary node method
Chen Shen-Shen†, , Wang Juan, Li Qing-Hua
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China

 

† Corresponding author. E-mail: chenshenshen@tsinghua.org.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11462006 and 21466012), the Foundation of Jiangxi Provincial Educational Committee, China (Grant No. KJLD14041), and the Foundation of East China Jiaotong University, China (Grant No. 09130020).

Abstract
Abstract

A scaled boundary node method (SBNM) is developed for two-dimensional fracture analysis of piezoelectric material, which allows the stress and electric displacement intensity factors to be calculated directly and accurately. As a boundary-type meshless method, the SBNM employs the moving Kriging (MK) interpolation technique to an approximate unknown field in the circumferential direction and therefore only a set of scattered nodes are required to discretize the boundary. As the shape functions satisfy Kronecker delta property, no special techniques are required to impose the essential boundary conditions. In the radial direction, the SBNM seeks analytical solutions by making use of analytical techniques available to solve ordinary differential equations. Numerical examples are investigated and satisfactory solutions are obtained, which validates the accuracy and simplicity of the proposed approach.

PACS: 02.60.Cb;02.60.Lj;46.25.–y;
Keyword:fracture mechanics;meshless method;semi-analytical;piezoelectric materials;
1. Introduction

The inherent coupling between mechanical and electrical behaviors means piezoelectric material is extensively used in smart structures and other applications, such as electromechanical sensors, ultrasonic transducers, buzzers and structural actuators.[1] A significant disadvantage of piezoelectric material, such as piezoelectric ceramics, is its brittleness. Therefore, a thorough understanding of the fracture behavior of piezoelectric material will have significant influence on its applications and may lead to device performance improvements. To solve the fracture problems of piezoelectric materials, some analytical methods[2,3] have been successfully used. However, to consider more realistic cases with complex geometries and loadings, numerical methods need to be used. Therefore, more and more efforts have been devoted to the research on analyzing fracture problems of piezoelectric material by utilizing the finite element method (FEM),[4,5] the boundary element method (BEM),[6–9] the extended finite element method,[10,11] and the scaled boundary finite element method (SBFEM).[12,13] It should be stressed here that the SBFEM, developed recently by Wolf and Song,[14] combines with the advantages of the FEM and the BEM. Only the boundary of the domain is discretized, no fundamental solution is required and singularity problems can be modeled rigorously. However, the SBFEM still requires boundary discretization, resulting in some inconvenience in the implementation. In order to avoid meshing, the meshless methods[15] have received more and more attention in the computational mechanics field in the past three decades. An attractive advantage of the meshless methods is that the approximate solution is constructed entirely based on a set of scattered nodes and the limitations related to mesh do not exist.

So far a wide variety of meshless methods have been proposed. In general, these methods can be classified as two categories, the boundary type and the domain type. Undoubtedly, the boundary-type meshless method is superior to the domain-type one because of its advantage of dimension reduction. Consequently, different boundary-type meshless methods have been proposed, such as the boundary node method (BNM),[16,17] the boundary face method,[18] the hybrid boundary node method,[19] the boundary cloud method,[20] the boundary element free method,[21,22] the Galerkin boundary node method,[23] and the scaled boundary node method (SBNM).[24] Of these, the SBNM does not require any singular integral nor fundamental solution, which constitutes a big contrast to other boundary-type meshless methods. With the scaled boundary coordinate system, meshless approximations in the circumferential direction enable the SBNM to convert the governing partial differential equations of various linear problems into ordinary differential equations. Through a matrix function solution technique,[12,13] these ordinary differential equations can be solved in a closed-form analytical manner. The moving Kriging (MK) interpolation[25,26] is utilized to generate the shape functions in the circumferential direction. Increased smoothness and continuity of the shape functions yield the solutions with higher accuracy. Moreover, another outstanding feature of the MK interpolation is that it is a passing node interpolation and thus no special techniques are required to impose the essential boundary conditions.

Motivated by the need to use the newly developed method for coupled-field analysis, a novel semi-analytical solution technique based on the SBNM is developed to calculate the stress and electric displacement intensity factors of piezoelectric materials in this paper. In this study, displacement and electric potential, strain and electric field, stress and electric displacement are combined together so that the governing equations of piezoelectric materials can be formulated in an elastic-like manner. This enables the scaled boundary meshless equation for piezoelectric materials to be derived conveniently by virtue of the virtual work principle. The impermeable boundary conditions are assumed here to model the electric boundary conditions along the crack faces. In order to avoid increasing the smoothness of the trial functions at corners, the MK interpolation is independently generated along each edge rather than the entire boundary. The solution of the SBNM is analytical in the radial direction, resulting in accurate and direct calculations of the stress and electric displacement intensity factors. Numerical examples are presented to validate the accuracy and efficiency of the proposed numerical approach.

2. Governing equations and boundary conditions

The governing equations and boundary conditions which form the foundation of piezoelectric materials are briefly summarized.[1–13] When the medium is transversely isotropic and the y axis is in the poling direction, the generalized plane strain constitutive equations can be written as

where is the extended stress, is the extended strain, and H is the material constant matrix. They are the following forms

where σx, σy, and τxy are the stress components; Dx and Dy represent the electric displacements; ɛx, ɛy, and γxy denote the strain components; Ex and Ey are the electric fields; c11, c13, c33, and c44 are the elastic constants; e31, e33, and e15 are the piezoelectric constants; h11 and h33 are the dielectric constants. The extended strain in Eq. (1) can be expressed in the form

where ū is named the extended displacement, ux and uy denote the displacement components, ϕ represents the electric potential, and L is the linear differential operator matrix and is in the following form:

If there are no body forces and no body charges, the equilibrium equations can be written in the form of

Furthermore, the corresponding boundary conditions for the piezoelectric boundary value problem are as follows:

where ni is the unit outward normal to the boundary, while ûi, t̂i, , and q̂ are the specified displacement, traction, electric potential, and surface charge, respectively.

3. Implementation of the scaled boundary node method
3.1. Brief description of the MK interpolation

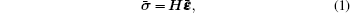
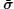
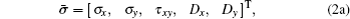
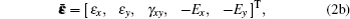
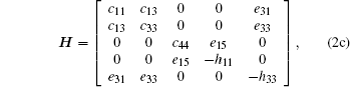
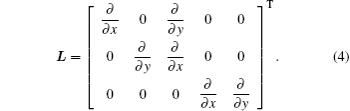
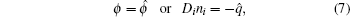
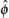
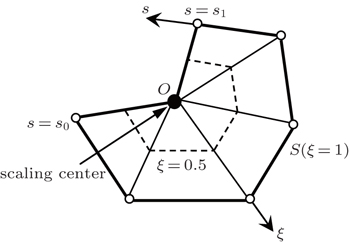
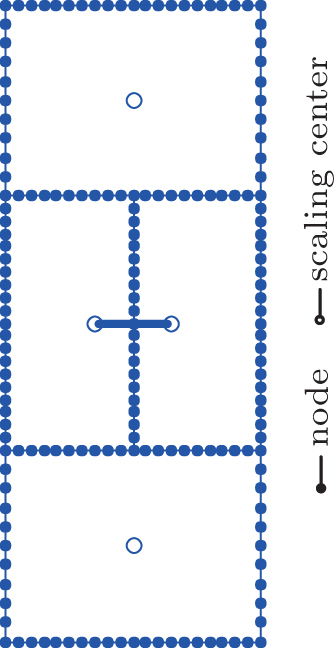
As already mentioned in Section 1, the MK interpolation[24–26] is utilized in this paper to approximate unknown fields in the circumferential direction. The trial functions are independently generated on piecewise smooth edges, which constitute the entire boundary S naturally. It is assumed that a set of scattered nodes si (i = 1,2, …,N) defined by a random function u(s) are distributed on a single edge, where s is the circumferential coordinate. If there are n scattered nodes in the interpolation domain, the function u(s) at point s is approximated in the form

where u = [ u(s1), u(s2), …, u(sn) ]T, and ϕI (s) is the MK shape function, which is in the form of

The matrices A and B in Eq. (8) can be written as

where I is a unit matrix of size n × n, and p(s) = [ 1 s ··· sm − 1 ]T is a complete monomial basis of order m. The matrix P has a size of n×m and can be expressed in the following form:

The matrix R and the vector r(s) can be expressed in an explicit form as

where R(si,sj) denotes the correlation function between any pair of nodes. In this paper, the commonly used Gaussian function is chosen as R(si,sj), namely

where rij = || si − sj ||, and θ > 0 is a given correlation parameter. In the present study, a linear basis pT(s) = (1 s) is used in all numerical computations. Obviously, the shape function ϕI (s) obtained here possesses the Kronecker delta property.

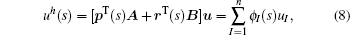
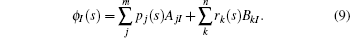
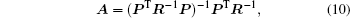
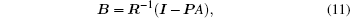
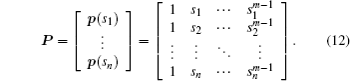
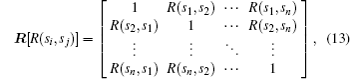
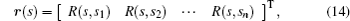
In meshless methods, it is necessary to define the interpolation domain for a point. In this work, the radius of the interpolation domain is calculated as follows:

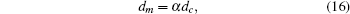
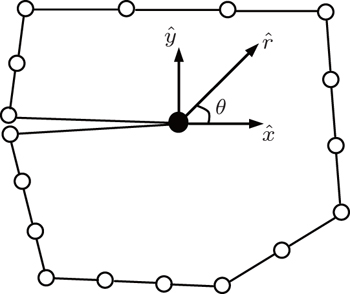
where dc is the minimum nodal spacing close to the interpolation point, while the coefficient α, taken as 4.0 here, represents a scaling factor.

3.2. Scaled boundary meshless equation in displacement and electric potential

As shown in Fig. 1, a scaled boundary coordinate system is introduced in the SBNM. The domain can be formed by the mapping of its boundary S with respect to a scaling center O, from which the entire boundary S is visible. The normalized radial coordinate ξ is a scaling factor, defined as being a value of zero at the scaling center and unity on the boundary, and the circumferential coordinate s measures the distance anticlockwise along the boundary. If the scaling center coincides with the origin of the Cartesian coordinate system, the conversion between the scaled boundary and Cartesian coordinate systems is as follows:[12–14]

where (x,y) denotes an arbitrary point on the boundary and (x̂,ŷ) refers to an interior point of the domain. With this geometric mapping, the linear differential operator matrix L in Eq. (4) is mapped to the scaled boundary coordinate system in the form of

where b1(s) and b2(s) respectively take the forms of

with

Fig. 1. Scaled boundary coordinate system.

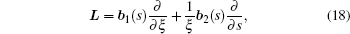
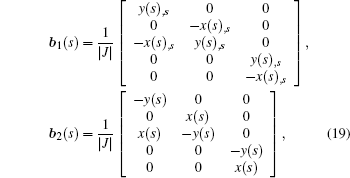
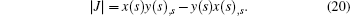
The solution for the extended displacements ū(ξ,s) at any point can be approximated by

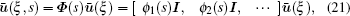
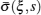
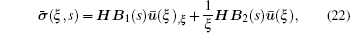
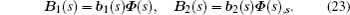
where ū(ξ) represents the nodal extended displacement function, ϕ1(s) is the meshless shape function defined in Eq. (9), and I is a unit matrix of size 3×3. Consequently, the extended stresses can be further expressed in terms of the scaled boundary coordinate system as

where B1(s) and B2(s) are in the following forms:

By applying the virtual work principle to elastostatics,[28] the scaled boundary meshless equation in extended displacement can be derived as

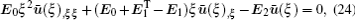
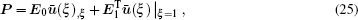
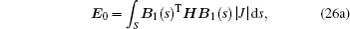
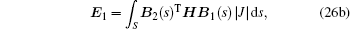
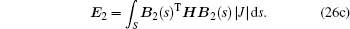
where P is the vector of extended equivalent nodal forces, and E0, E1, and E2 are the coefficient matrices with the following forms:

3.3. Solution procedure

The homogeneous second-order differential equations in Eq. (24) can be solved analytically by a matrix function solution technique.[12,13,27] This technique first converts Eq. (24) into a system of first-order ordinary differential equations as

where the variable X(ξ) and the Hamiltonian matrix Z are given as follows:

with q̄(ξ) defined by

Block diagonal Schur decomposition of the matrix Z is performed, which yields

with the transformation matrix ψ partitioned conformably into 2N block matrices as

where I in Eq. (30) is a unit matrix of size 3×3. S is a block-diagonal matrix in real Schur form and is sorted in ascending order of the real parts of its eigenvalues. Note that the extended nodal force modes are zero due to the fact that are the three rigid body modes.

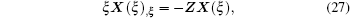
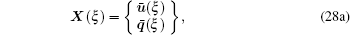
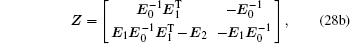
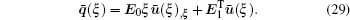
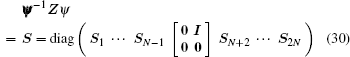
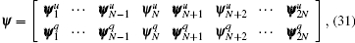
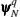
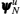
The stiffness matrix Kb of a bounded domain (0 ≤ ξ ≤ 1) can be accordingly calculated as

and the equilibrium requirement becomes

Once the essential boundary conditions are imposed, the extended nodal displacements on the boundary ū(ξ = 1) can be determined by the solution of Eq. (33). It is clear that no special treatment is required to impose the essential boundary conditions due to shape functions possessing the Kronecker delta property. In the case of a bounded domain defined by 0 ≤ ξ ≤ 1, the extended displacements at the scaling center must remain finite and therefore ū(ξ) can be written as

where the integration constants c = { c1, c2, …, cN }T are determined by

Substitution of Eq. (34) into Eq. (22) results in the extended stresses at any point in the domain with the following form:

where ψσi (s) denotes the extended stress mode and is defined as

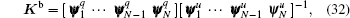
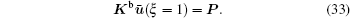
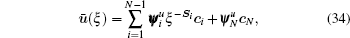
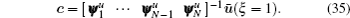
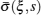
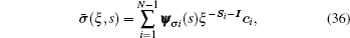
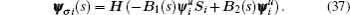
As shown in Eqs. (36) and (37), the extended stress solutions of the SBNM are analytical in the radial direction, which enables us to calculate the stress and electric displacement intensity factors directly based on their definitions by choosing the scaling center at the crack tip. For a crack in the homogeneous piezoelectric material, the stress and electric displacement intensity factors KI, KII, and KD are defined as follows:

where r̂ and θ are the polar coordinate centered at the crack tip as shown in Fig. 2.

Fig. 2. A cracked domain modeled by the scaled boundary node method.
4. Numerical examples

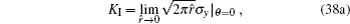
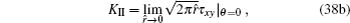
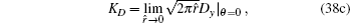
In order to validate the proposed solution technique, three numerical examples are presented in this section to perform two-dimensional fracture analysis of piezoelectric material. Under the plane strain assumption, the stress and electric displacement intensity factors are computed and compared with other previously reported solutions. In the computation, the piezoelectric materials of PZT-5H and PZT-4 are considered and their elastic, piezoelectric and dielectric constants are given in Table 1, where the elastic constants ci j are in 109 N/m2, the piezoelectric constants ei j are in units C/m2, and the dielectric constants hi j are in 10− 9 C/(V· m).

Material constants of piezoelectric materials.

c11 c13 c33 c44 e31 e33 e15 h11 h33
PZT-5H 126 84.1 117 23 −6.5 23.3 17.44 15.03 13.0
PZT-4 139 74.3 115 25.6 −5.2 15.1 12.7 6.45 5.62

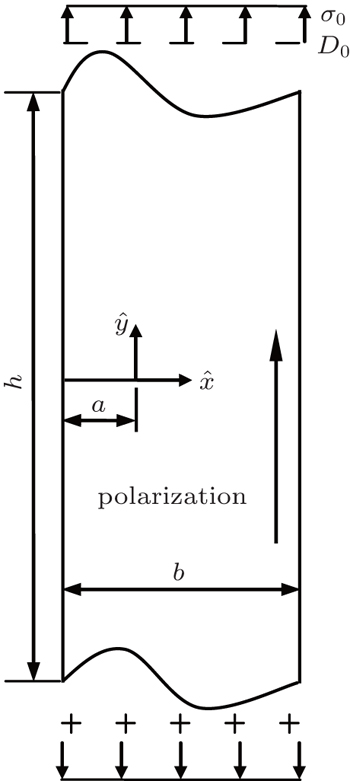
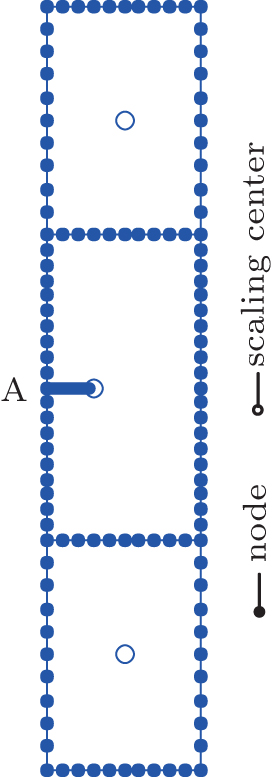
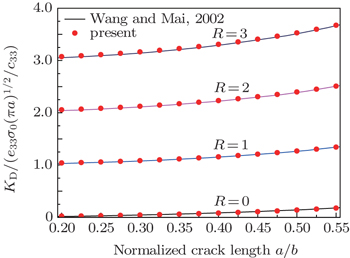
4.1. A piezoelectric strip with an edge crack

A b × h piezoelectric strip containing an edge crack of length a as shown in Fig. 3, is taken into consideration in the first example. The strip is assumed to be under a combined action of a uniform tension σ0 and a uniform electric displacement D0 at the far ends, applied in the y direction. The crack is perpendicular to the poling direction and the piezoelectric material used in this example is PZT-5H. The same problem was analyzed by Wang and Mai[29] by using the Fourier transforms technique.

Fig. 3. Piezoelectric strip with an edge crack.

In order to simulate the infinite height, the ratio between the height h and the width b is chosen to be 5, which is relatively large. As shown in Fig. 4, this strip is modeled with three subdomains including 119 nodes totally. In the subdomain with the crack, the scaling center is chosen at the crack tip and no discretization on the two crack faces is required. The computational results of the normalized intensity factors KI and KD are depicted in Figs. 5 and 6 respectively, where R = D0 c33/(e33 σ0) = 0,1,2,3. Attractively, the present results almost coincide with those reported by Wang and Mai,[29] which illustrates the correctness and the accuracy of the present method. It is also found that there is no significant effect observed on the stress intensity factor when the applied electric displacement load is varied. However, the increasing electric displacement load can enhance the electric displacement intensity factor.

Fig. 4. SBNM mesh for the piezoelectric strip with an edge crack.
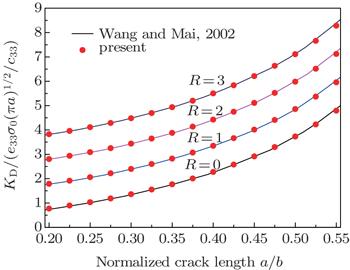
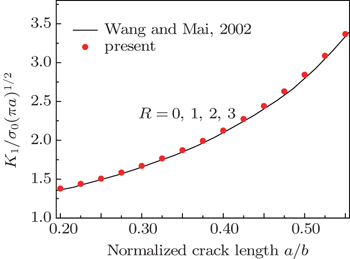Fig. 5. Plots of normalized stress intensity factor KI versus normalized crack length for the piezoelectric strip with an edge crack for different values of R.
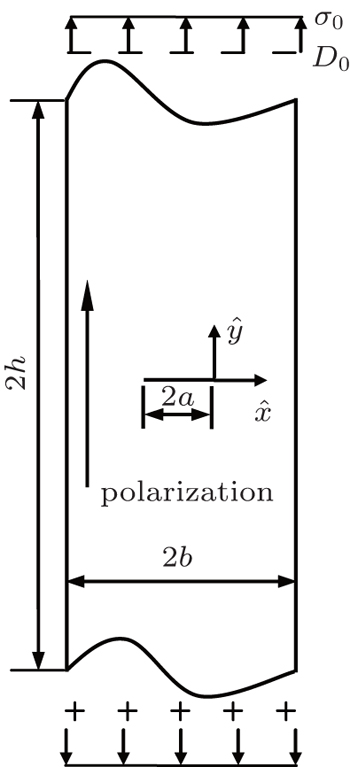
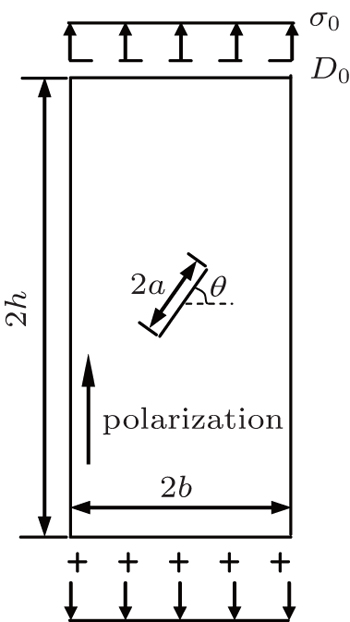
Fig. 6. Plots of normalized electric displacement intensity factor KD versus normalized crack length for the piezoelectric strip with an edge crack for different values of R.
4.2. A piezoelectric strip with a central crack

The second example deals with a piezoelectric PZT-5H strip of width 2b and height 2h containing a central crack of length 2a. The geometric configuration and the poling direction are shown in Fig. 7. The strip is loaded by a uniform tension σ0 and a uniform electric displacement D0 at the far ends along the y direction. The ratio between the mechanical and the electrical load is given as R = D0 c33/(e33 σ0).

Fig. 7. Piezoelectric strip with a central crack.

When modeling, this strip is truncated into a finite plate with the height h = 5b. Figure 8 shows the nodes that are used for solving this example. Four subdomains are employed here and their scaling centers are also shown in Fig. 8. Note that two overlapping nodes are addressed at the center of this strip. For different values of R, the normalized intensity factors KI and KD versus the normalized crack length are plotted in Figs. 9 and 10. Also shown in these two figures are the results of Wang and Mai.[29] A comparison between both results shows a very good agreement, which further confirms that the present method can be successfully used to analyze two-dimensional fracture problems of piezoelectric materials. Moreover, as in the previous example, the electric displacement intensity factor also increases while negligible influence is observed for the stress intensity factor provided that the electric displacement load increases.

Fig. 8. SBNM mesh for the piezoelectric strip with a central crack.
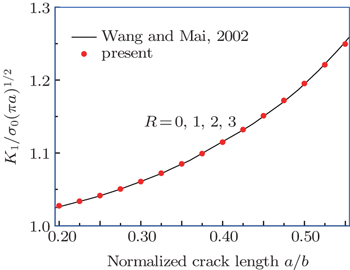Fig. 9. Plot of normalized stress intensity factor KI versus normalized crack length for the piezoelectric strip with a central crack for different values of R.
Fig. 10. Plots of normalized electric displacement intensity factor KD versus normalized crack length for the piezoelectric strip with a central crack for different values of R.
4.3. An inclined central crack in a rectangular piezoelectric plate

A piezoelectric PZT-4 plate of width 2b and height 2h with a θ=45° inclined central crack of length 2a is considered here as depicted in Fig. 11. This plate is subjected to a uniform tension σ0 or electric displacement D0 along the y direction. For comparison, the dimensions of the plate are adopted as b = 5a and h = 2b, which are the same as those in Refs. [1] and [6]. There are two subdomains in this example and in each subdomain the entire boundary contains five edges, of which two edges are of the first kind, two edges are of the second kind, and one edge is of the third kind. A series of evenly spaced nodes are introduced to subdivide the edges of the first, second and third kind into n, 2n, and 4n sections, respectively. For the case of n = 10, the mesh of this problem is shown in Fig. 12.

Fig. 11. An inclined central crack in a rectangular piezoelectric plate.
Fig. 12. SBNM mesh for the piezoelectric plate with an inclined central crack.

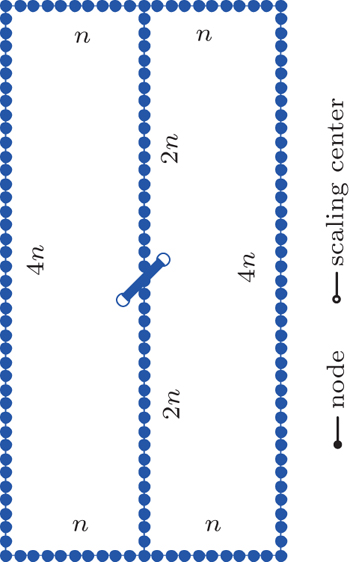
To verify the effectiveness of the present method, the convergence properties are examined by increasing the number of sections in each edge. For different values of n, the normalized intensity factors ahead of the left crack tip are computed under the uniform tension load σ0 and listed in Table 2. It is observed that the results obtained from n = 30 and n = 40 are almost indistinguishable and thus n = 30 is employed here. When the uniform σ0 and D0 are used respectively, the normalized intensity factors ahead of the left crack tip are computed and the numerically detailed comparisons with available earlier results are summarized in Tables 3 and 4. It is found that our results, in general, agree well with those available in the literature. This further demonstrates the effectiveness of the present method.

Table 2.

Comparison among normalized intensity factors obtained from different values of n.

.
Table 3.

Comparison among normalized intensity factors for the rectangular plate under σ0.

.
Table 4.

Comparison among normalized intensity factors for the rectangular plate under D0.

.
5. Conclusions

In this paper, a reliable and efficient solution technique based on the SBNM is extended for fracture analysis in plane piezoelectricity. In the sense of satisfying the equilibrium requirement in the strong form in the radial direction, the SBNM can be viewed as a semi-analytical numerical method. This enables the calculation of the stress and electric displacement intensity factors of piezoelectric materials directly from their definitions without any post-processing. Through the use of the MK interpolation, no mesh generation is necessary and only a nodal data structure on the boundary is required in the SBNM. In comparison with the conventional scaled boundary FEM, the MK interpolation results in superior accuracy, rapid convergence and smooth stress and electric displacement solutions. Besides, it seems that the implementation of the SBNM is convenient because the Kronecker delta property of the MK shape functions can simplify the enforcement of the essential boundary conditions greatly. The results of all the numerical examples demonstrate the effectiveness and robustness of the developed approach to analyzing the two-dimensional fracture problems of piezoelectric materials.

Reference
1Sheng NSze K YCheung Y K 2006 Int. J. Numer. Method Eng. 65 2113
2Pak Y E 1992 Int. J. Fract. 54 79
3Gao C FFan W Y 1999 Int. J. Solids Struct. 36 2527
4Kumar SSingh R 1996 Acta Mater. 44 173
5Gruebner OKamlah MMunz D 2003 Eng. Frac. Mech. 70 1399
6Pan E 1999 Eng. Anal. Bound. Elem. 23 67
7Rajapakse R K N DXu X L 2001 Eng. Anal. Bound. Elem. 25 771
8Garcia-Sanchez FSaez ADominguez J 2005 Comput. Struct. 83 804
9Sheng NSze K Y 2006 Comput. Mech. 37 381
10Bui T QZhang C Z 2012 Comput. Mater. Sci. 62 243
11Liu PYu T TBui T QZhang C Z 2013 Comput. Mater. Sci. 69 542
12Li CMan HSong C MGao W 2013 Eng. Fract. Mech. 97 52
13Li CMan HSong C MGao W 2013 Compos. Struct. 101 191
14Song CWolf J 1997 Comput. Methods Appl. Mech. Eng. 147 329
15Cheng Y MPeng M JLi J H2005Acta Mech. Sin.37719(in Chinese)
16Mukherjee Y XMukherjee S 1997 Int. J. Numer. Method Eng. 40 797
17Kothnur V SMukherjee SMukherjee Y X 1999 Int. J. Solids Struc. 36 1129
18Zhang J MQin X YHan XLi G Y 2009 Int. J. Numer. Method Eng. 80 320
19Zhang J MTanaka MMatsumoto T 2004 Int. J. Numer. Method Eng. 59 1147
20Shrivastava VAluru N R 2004 Int. J. Numer. Method Eng. 59 2019
21Peng M JCheng Y M 2009 Eng. Anal. Bound. Elem. 33 77
22Cheng Y MPeng M J 2005 Sci. China- Ser. G Phys., Mech. Astron. 48 641
23Li X L 2011 Int. J. Numer. Method Eng. 88 442
24Chen S SLi Q HLiu Y H 2012 Chin. Phys. 21 110207
25Gu L 2003 Int. J. Numer. Method Eng. 56 1
26Zheng B JDai B D 2011 Appl. Math. Comput. 218 563
27Song C 2004 Comput. Methods Appl. Mech. Eng. 193 2325
28Deeks A JWolf J P 2002 Comput. Mech. 28 489
29Wang B LMai Y W 2002 Int. J. Solids Struc. 39 4501