|
|
† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the Science and Technology Program of Guangdong Province, China (Grant Nos. 2014B010106005, 2013B051000077, and 2015A050502047) and the Science and Technology Program of Guangzhou City, China (Grant No. 201508030018).
With the combination of the dielectric loss of the carbon layer with the magnetic loss of the ferromagnetic metal core, carbon-coated nickel (Ni(C)) nanoparticles are expected to be the promising microwave absorbers. Microwave electromagnetic parameters and reflection loss in a frequency range of 2 GHz–18 GHz for paraffin-Ni(C) composites are investigated. The values of relative complex permittivity and permeability, the dielectric and magnetic loss tangent of paraffin-Ni(C) composites are measured, respectively, when the weight ratios of Ni(C) nanoparticles are equal to 10 wt%, 40 wt%, 50 wt%, 70 wt%, and 80 wt% in paraffin-Ni(C) composites. The results reveal that Ni(C) nanoparticles exhibit a peak of magnetic loss at about 13 GHz, suggesting that magnetic loss and a natural resonance could be found at that frequency. Based on the measured complex permittivity and permeability, the reflection losses of paraffin-Ni(C) composites with different weight ratios of Ni(C) nanoparticles and coating thickness values are simulated according to the transmission line theory. An excellent microwave absorption is obtained. To be proved by the experimental results, the reflection loss of composite with a coating thickness of 2 mm is measured by the Arch method. The results indicate that the maximum reflection loss reaches −26.73 dB at 12.7 GHz, and below −10 dB, the bandwidth is about 4 GHz. The fact that the measured absorption position is consistent with the calculated results suggests that a good electromagnetic match and a strong microwave absorption can be established in Ni(C) nanoparticles. The excellent Ni(C) microwave absorber is prepared by choosing an optimum layer number and the weight ratio of Ni(C) nanoparticles in paraffin-Ni(C) composites.
With the development of wireless communications, microwave absorbers are becoming increasingly important for applications in special fields such as silent rooms, radar systems and the military.[1–4] Nano-materials, as a new type of microwave absorber, have received more and more attention due to their special properties such as surface effect, quantum size effect and small size effect. Until now, microwave nano-absorbers, including nano-metals, nano-alloys, nano-oxides, nano-conductive polymers, the composites of nano-metals and insulation media and so on, have been extensively studied.[5–10] The potential microwave absorber with nanowire microstructure has a maximum absorption of 8.37 dB when the concentration of the ZnO nanowires is 6%. It has also been reported that the maximum absorption is enhanced up to 12.28 dB when the concentration of ZnO increases 7%.[9] In particular, many efforts have been made to study the nano-materials with the special microstructures. Qiu et al.[10] reported that a cagelike ZnO/SiO2 had been prepared, and the properties of microwave absorption had been studied. It has been found that the maximum absorption of the cagelike ZnO/SiO2 is 10.68 dB at a frequency of 12.79 GHz, and the absorption range is from 10 GHz to 18 GHz under −6.0 dB. Ferrite is a kind of magnetic loss absorbing material with excellent performance.[11–13] To solve the heavy mass problem of the traditional spinel ferrite used as a microwave absorber, Huang et al.[12] have synthesized cobalt zinc spinel ferrite nanofiber by the electrospinning method. The microwave absorbing coating containing 15 wt% of Co0.6Zn0.4Fe2O4 ferrite nanofiber showed that the reflection loss is less than −10 dB in the whole X-band. Cho and Kim[13] investigated the microwave absorbing characteristics in grid-shaped rubber composite sheets containing Ag-coated Ni–Zn ferrite particles. In the grid-type absorber with an optimum air cavity volume rate, the reflection loss is 30 dB at 10.5 GHz when a small layer thickness is about 2 mm. The proposed grid-type microwave absorber has advantages in reduced weight in comparison with conventional ferrite composite absorbers.
Carbon-based materials have good dielectric losses, light weights and broadband microwave absorptions. The carbon nanotubes (CNTs) have been investigated in the field of microwave absorption.[14–22] Zou et al.[20] reported that multi-walled nanotubes (MWNTs) filled with Ni nanowire have a good microwave absorption. It has been found that the real and imaginary parts of permittivity and permeability in Ni nanowire filled MWNTs composites increase with the increasing of Ni nanowire filled MWNT concentration. The Ni nanowire filled MWNTs/paraffin composite achieves a reflection loss below –10 dB at 6.4 GHz∼11 GHz, and the minimum value is −23.1 dB at 8.0 GHz. The microwave absorption of Ni nanowire filled MWNTs/paraffin composites is attributed to both dielectric and magnetic loss. The microwave-absorbing peaks of composites shift towards low frequencies with an increase in the concentration of Ni nanowire filled MWNTs. Multi-walled carbon nanotubes (MWCNTs)-polyimide matrix can be considered as a high temperature microwave absorbing material with a broadband.[22] When the percentage of MWCNTs is 5%, the −10-dB absorption bandwidth could reach 1.3 GHz, with a microwave absorber thickness of 2.1 mm in a frequency range from 8 GHz to 12 GHz, while the bandwidth below −10 dB is 2.04 GHz with a microwave absorber thickness of 1.7 mm at a temperature of 373 K.
The core (metal)/shell (carbon) microstructure may be an excellent structure for microwave absorption due to the synergistic effect of the material interfaces between the metal cores and the carbon shells. Zhang et al.[23] have reported that Ni(C) nanocapsules have a better electromagnetic match due to the existence of carbon shells and the particular “core/shell” microstructures. According to the transmission line theory, by using the measured relative complex permeability and permittivity, the maximum reflection loss of Ni(C) nanocapsules is calculated to be equal to 32 dB at 13 GHz, and the absorption range below −10 dB is from 11.2 GHz to 15.5 GHz with 2-mm thickness of the microwave absorber. It has been also found that a natural resonance appearing at 5.5 GHz in Ni(C) nanoparticles, which is dominant among microwave absorption properties of Ni(C) nanocapsules, leads to an increased surface anisotropic energy for nanosized particles. Wang et al.[24] reported that according to transmission line theory, a reflection loss of −25 dB in CoNi@C nanocapsules is derived in a frequency range of 5 GHz–17 GHz, and the absorber thickness is between 2.0 mm and 4.8 mm. CoNi@C nanocapsules have the more excellent electromagnetic-wave absorption in a frequency range of 5 GHz–17 GHz. The CoNi@C nanocapsules have dual dielectric relaxation of the permittivity and multiple magnetic resonances of the permeability. Although the current reports on the microwave absorption performance of core (metal)/shell (carbon) microstructure are mostly restricted to simulation by transmission line theory, there are few reports on the experimental absorption. It is important to compare the experimental results with simulation results for evaluating the microwave reflectivity of nano-materials with core/shell microstructure. In the present paper, the experimental absorption of Ni(C) composites is measured and compared with the theoretical simulation result. It is found that the theoretical simulation result can be in good agreement with the measured absorption peak frequency position.
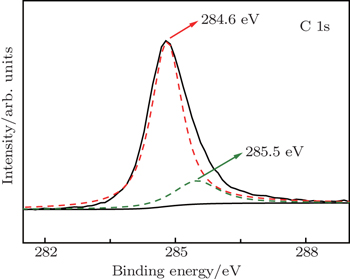
As for the Ni/C ratio, all the carbon-coated Ni metal nanoparticles were prepared by the carbon arc discharge method in this paper. The carbon arc discharge was generated by discharging between two electrodes with a DC current of 150 A at 60-V voltage under an argon pressure of 10 kPa. The distance between the electrodes was 3 mm–4 mm. An anode of 25 mm in diameter was prepared with a uniform mixture of micron-sized Ni powders (purity 99.9%) and micro-sized graphite powders (purity 99.0%) in a 50% Ni/C weight ratio. The morphology and microstructure of the sample were examined by transmission electron microscopy (TEM), x-ray diffraction (XRD), and x-ray photoelectron spectroscopy (XPS). Ni(C) nanoparticles and sodium dodecyl benzene sulfonate (SDBS), which were mixed according to a certain proportion, were added into a certain amount of deionized water. The mixed solution was refluxed for 30 min at room temperature, and then the precipitates, which were Ni(C) nanoparticles mixed with SDBS, were separated out of the solution. The slurry of Ni(C) nanoparticles were prepared by adding these pre-treated Ni(C) nanoparticles into the anhydrous ethanol. The slurry of Ni(C) nanoparticles were dispersed by methods of electric stirring for 10 min and ultrasonic dispersion for 10 min successively.
The outer and inner diameters of each of the toroidal shaped coaxial samples of paraffin-Ni(C) were 7 mm and 3 mm respectively. The coaxial samples were prepared by dispersing uniformly the Ni(C) nanoparticles in a paraffin matrix, and were transparent for an electromagnetic wave. In order to measure the electromagnetic parameters, the coaxial samples were pressed into a cylindrical compact. The system of an AV3618 vector network analyzer was used to measure the electromagnetic parameters.
Pre-treated Ni(C) nanoparticles, epoxy resin and anhydrous ethanol were used as a filler, matrix and dispersion medium, respectively. The Ni(C) nanoparticles/epoxy resin was prepared by dispersing the slurry of Ni(C) nanoparticles into epoxy resin. These coating samples were painted onto the 180 mm ×180 mm standard aluminium plate, which are shown in Fig.
 | Fig. 1. Microwave absorption plate of Ni (C) mixed epoxy resin (a) and the standard aluminium plate (b). |
With the combination dielectric loss of the carbon layer and magnetic loss of the ferromagnetic metal cores, Ni(C) nanoparticles are expected to be promising microwave absorbers. The properties of microwave absorption in carbon-coated nanoparticles can be calculated by reflection loss based on transmit-line theory.[25,26] The measured electromagnetic parameters of paraffin-Ni(C) composites are substituted into the following electromagnetic equations (
According to the transmission line theory, the input impedance of the layers is Zin(K) (K = 1, 2, …,N). The input impedance of each layer can be calculated from the following formula:
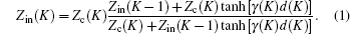
Because at the bottom is a metal plate, Zin(0) = 0 which is the impedance of free space. Zc(K) and γ(K) can be calculated from Eqs. (
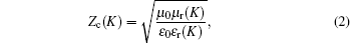
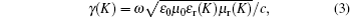
When the electromagnetic wave is incident vertically on the interface, of which the input impedance through the free space is Z0 = (μ0/ε0)1/2, part of it is reflected, and the rest enters the absorber. The absorber reflection factor is determined by the following formula:
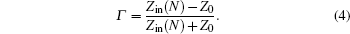
Reflection rate (R) of the N-layer absorbing material is calculated from the following formula:
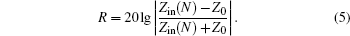
Figure
 | Fig. 2. TEM images of the Ni(C) nanoparticles. |
Figure
 | Fig. 3. X-ray diffraction patterns of Ni(C) nanoparticles. |
 | Fig. 4. XPS patterns of Ni(C) nanoparticles. |
Figure
 | Fig. 5. Hysteresis loops of Ni(C) nanoparticles at T = 304 K. |
Figure
 | Fig. 6. Variations of (a) the real part and (b) the imaginary part of the relative complex permittivity of paraffin-Ni(C) wax composites with frequency for different percentages of Ni(C) in composites. |
According to the loss mechanism of absorbing materials for the electromagnetic wave, absorbing materials can be divided into two kinds of materials: the dielectric medium and magnetic medium. The dielectric medium type of absorbing material, which produces electric polarization, absorbs electromagnetic wave energy under the action of electromagnetic field (dielectric loss). Likewise, the magnetic medium type of absorbing material, which produces magnetic polarization, absorbs electromagnetic wave energy under the action of an electromagnetic field (magnetic loss), such as magnetic hysteresis, domain-wall displacement, natural-resonance and eddy-current loss. The Ni(C) nanoparticle is a nanocapsule composite with the shell of a dielectric loss type and the nucleus of a magnetic loss type, and may establish a suitable electromagnetic matching in the microstructure for electromagnetic wave absorption in the gigahertz range. Previous reports have indicated that the surface-anisotropy field in the FeNi(C) nanoparticles is larger than that in the FeNi nanoparticles, which leads to a higher natural-resonance frequency.[27] The same phenomenon has been found in other nanocapsules.[28–30]
Some similar fluctuation peaks in the ε″ curves of the Ni(C) nanoparticles are dielectric loss peak (ε″) and attributed to various polarizations. The maximum imaginary part value of relative complex permittivity (ε″) is 19 at 2 GHz. Han et al.[31] reported a similar permittivity spectrum of the carbon-encapsulated FeCo system. Considering the special core/shell microstructure of the Co(C) nanoparticles, a reasonable explanation for observed permittivity curves is that the dipole polarization is dominant at a higher frequency and the space charge polarization plays an important role at a lower frequency.[24,32,33] Similar observations were previously reported in carbon-encapsulated iron nanoparticles.[6]
On the other hand, according to the free electron theory, ε ≈ 1/2πε0ρ f, where ρ is the electrical resistivity.[23] Obviously, low ε″ corresponds to high electrical resistivity. It can be concluded that the electrical resistivity of Ni(C) composites is higher than that of nano-nickel (ρ ∼ 10−3 Ω·cm) due to capsuled carbon (ρ ∼ 10−1 Ω·cm). The protective carbon shells on the surface of Ni nanoparticles can also effectively disperse Ni(C) nanoparticles in paraffin[31,32] so that the perfect performance of Ni(C) composites can be realized.
It is proposed that the core/shell microstructure of the Ni(C) nanoparticles can improve the microwave absorption of nano-carbon particles. The orientation (dipole) polarization and space charge polarization (interfacial polarization) are considered as relaxation polarization and produced larger absorption in the measured frequency range of 2 GHz–18 GHz. The interfacial polarization is also believed to give Co(C) strong dielectric loss, which has been proved in previous work.[28,33,34] The space charge polarization (interfacial polarization) often occurs in an inhomogeneous medium, such as the interface between the core and the shell. Actually, grain boundary, phase boundary and impurity defects can also become an obstacle to the free charge movement, so free charge accumulation is produced and space charge polarization is formed. When Ni(C) is subjected to an electromagnetic field, the space charge polarization occurs at the interface between the amorphous carbon shell and the inner nickel core.
The curves of relative complex permeability in the paraffin-Ni(C) composites at frequencies ranging from 2 GHz to 18 GHz are shown in Fig.
 | Fig. 7. Plots of (a) the real part and (b) imaginary part of relative complex permeability of paraffin-Ni(C) wax composites versus frequency for 10 wt%, 40 wt%, 50 wt%, 70 wt%, and 80 wt% Ni(C) in composites. |
As shown in Fig.
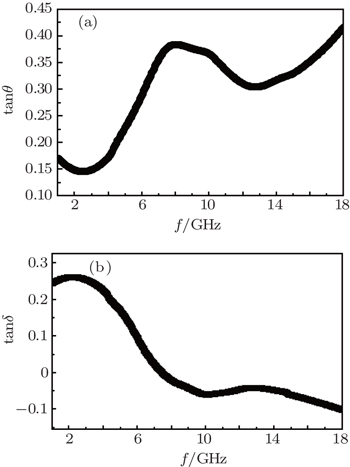 | Fig. 8. Plots of (a) dielectric loss tangent and (b) magnetic loss tangent of 50-wt% Ni(C) nanoparticles in composites versus frequency. |
In the Ni(C) nanoparticles, the inner nickel cores are separated by the outer carbon shell, so that the direct exchange interactions between magnetic metallic nickel cores are negligible, and the dipolar interaction is the main effect.[25,36] Without the protection of the carbon shell, the direct contact between the metallic nickel cores would take place, and the resulting eddy current would lead to the decrease of μ′ at a lower frequency.[26] The carbon shells between the nickel nanoparticles act as a barrier that effectively reduces the effect of the eddy current in the GHz frequency range. As mentioned previously, Ni(C) has a high electric resistivity, and the eddy current loss is reduced due to the outer carbon shells.[35,37] The Ni(C)/paraffin composite is mainly due to natural resonance instead of magnetic hysteresis, domain-wall displacement, and eddy current loss.
The relationship between the dielectric loss tangent (tanθ) and the frequency of paraffin-Ni(C) composites with 50-wt% Ni(C) nanoparticles is shown in Fig.
 | Fig. 9. (a) Curves of reflection loss versus frequency for 40 wt%–80 wt% Ni(C) in composites coating with 3-mm thickness, and (b) curves of reflection loss versus frequency for 50 wt% Ni(C) in composites coating with 2 mm–4 mm thickness. |
According to the theoretical simulation, the curves of the reflection rate in paraffin-Ni(C) composites with 40% −80% wt% Ni(C) nanoparticles are shown in Fig.
Based on the theoretical simulation, the reflection rate curves of paraffin-Ni(C) composites with 50% Ni(C) nanoparticles and the thickness values of 2, 3, and 4 mm, respectively, are shown in Fig.
Generally, the excellent microwave absorbers result from the efficient complementarity between the relative complex permittivity and permeability of the material. The existence of carbon shells and magnetic Ni cores for Ni(C) nanoparticles is favourable to setting up an excellent electromagnetic match. Based on the above measured data of relative complex permeability and permittivity, a simulation of reflection loss is carried out with 2-mm thickness microwave absorbing coating consisting of paraffin-Ni(C) composites and calculated theoretically the reflection loss according to the transmit-line theory.[38,39] Figure
 | Fig. 10. Practical reflection loss versus frequency for 2-mm-thick Ni(C)/resin composites coating. |
To further prove theoretical simulation of the excellent microwave absorption in Ni(C) nanoparticles, epoxy resin-Ni(C) microwave absorption is prepared by dispersing the Ni(C) nanoparticles in epoxy resin and painting them onto the aluminum plate. The coating thickness is 2 mm and the weight percentage of Ni(C) is 50 wt%. As shown in Fig.
In this study, we can see that the relative complex permittivity and permeability of paraffin-Ni(C) composites increase with the increase of the weight percentage of Ni(C) in paraffin-Ni(C) composites. The paraffin-Ni(C) composites exhibit excellent microwave absorption, which is attributed to the combination of the dielectric loss of shells and the magnetic loss of cores arising from the core and shell microstructure of Ni(C) nanoparticles. The absorption of paraffin-Ni(C) composites is mainly due to natural resonance instead of magnetic hysteresis, domain-wall displacement, and eddy current loss.
As for the 50-wt% Ni(C) nanoparticles in paraffin-Ni(C) composites, the simulated results indicate that the maximum theoretical reflection loss reaches −60 dB at 8 GHz and the absorption frequency range under −10 dB is over 5 GHz for the thickness of 3 mm. When the thickness decreases to 2 mm, the maximum theoretical reflection loss is observed to be −32 dB at 12.5 GHz, suggesting that reducing the thickness of the paraffin-Ni(C) composite will be beneficial to the shift of the absorption peak toward the high frequency. The experimental results show that the maximum reflection loss is −26.73 dB at 12.7 GHz and the absorption bandwidth less than −10 dB is 4 GHz with an absorption layer of 2-mm thickness. Theoretical simulation results are well consistent with the measured absorption peak frequency position. The excellent Ni(C) nanoparticles microwave absorber can be prepared by choosing an optimum layer number and weight percentage of Ni(C) nanoparticles in the composites.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 |
