† Corresponding author. E-mail:
Projected supported by the National High Technology Research and Development Program of China (Grant No. 2012AA011603) and the National Natural Science Foundation of China (Grant No. 61372172).
Sparse-view x-ray computed tomography (CT) imaging is an interesting topic in CT field and can efficiently decrease radiation dose. Compared with spatial reconstruction, a Fourier-based algorithm has advantages in reconstruction speed and memory usage. A novel Fourier-based iterative reconstruction technique that utilizes non-uniform fast Fourier transform (NUFFT) is presented in this work along with advanced total variation (TV) regularization for a fan sparse-view CT. The proposition of a selective matrix contributes to improve reconstruction quality. The new method employs the NUFFT and its adjoin to iterate back and forth between the Fourier and image space. The performance of the proposed algorithm is demonstrated through a series of digital simulations and experimental phantom studies. Results of the proposed algorithm are compared with those of existing TV-regularized techniques based on compressed sensing method, as well as basic algebraic reconstruction technique. Compared with the existing TV-regularized techniques, the proposed Fourier-based technique significantly improves convergence rate and reduces memory allocation, respectively.
Nowadays, x-ray computed tomography (CT) has been widely used in clinical and industrial applications.[1] The involved x-ray radiation has also attracted increasing concern. Low-dose imaging has become a major challenge in the CT field.[2–4] The radiation dose in the data acquisition process can be reduced in two ways: by decreasing the current of the x-ray source and by reducing the number of projections. However, the details of an imaging object may be ignored with decreased scanning current. Therefore, the sparse scanning imaging process has become popular on the premise that it ensures reconstruction quality.
Research on sparse scanning has been conducted over decades. Given the low number of projections for the Tuy–Smith condition,[5,6] which prescribes a number limit for an accurate reconstruction. Hence, to obtain ideal results through analytic reconstruction methods is difficult, such as the filtered back-projection (FBP)[7] algorithms, which creates numerous artifacts because of the data inconsistency of sparse-view CT measurements. In fact, to the ill-posed problem, iterative reconstructions are currently the primary, widely used method of solving sparse projections. However, tolerating these methods is difficult because of their time-consuming and high-memory allocation in the spatial domain.
By contrast, the Fourier-based reconstruction method has advantages, such as high computational efficiency and low memory usage. These excellent properties are mainly due to fast Fourier transform (FFT). Various methods have been developed in accordance with central slice theorem.[8] In 1987, Peng et al.[9] derived fan-beam direct Fourier method by rebinning a fan to a parallel projection; this method has fewer operations than filtered convolution back-projection. In 2006, Fessler et al.[10] presented a projection method for fan-beam tomography based on non-uniform FFT (NUFFT), which significantly improves the speed of iterative reconstruction. In 2014, Zhao et al.[11] developed the generalized Fourier slice theorem and avoided the interpolation for fan beam rebinning.
However, the aforementioned Fourier methods are aimed at all angle projection data, and sparse-view reconstruction remains a challenge in the Fourier domain. Fortunately, CS-based iterative reconstruction[12–14] draws significant interest because of its beneficial potential in under-sampled CT reconstruction. This relatively recent innovation in signal processing allows image recovery from projections fewer than those required by the Nyquist sampling theorem. Reconstruction research on compressed sensing mainly focuses on the development in the spatial domain. In 2008, Pan et al.[15] proposed adaptive decent methods via a projection onto convex sets (POCS), which is conventionally used for algebraic reconstruction techniques (ART). Afterwards, the simultaneous ART (SART)[16] that is combined with total variation (TV) regularization, namely SART–TV,[17] improves reconstruction image quality and accelerates convergence. In 2013, the idea of alternating direction method (ADM) to solve constrained TV minimization was introduced by Zhang et al.,[18] which is superior to other spatial algorithms in image quality. In 2014, Wang et al.[19] reviewed basic conclusions and classical algorithms in sparse optimization in few-view reconstruction and predicted the future research direction of sparse optimization based few-view reconstruction for CT image reconstruction.
The theory of compressed sensing also offers new perspectives for Fourier-based iterative reconstruction. The related studies have also inspired the flourishing research in the compressive sensing area. In 2014, Choi et al.[20] presented a Fourier-based CS technique, which provides a fast convergence rate for parallel beam CT reconstruction in sparse view. In 2015, Yan et al.[21] proposed a reconstruction method of NUFFT-based iterative image reconstruction via alternating direction TV minimization (ADTVM) for sparse-view parallel beam CT. The above work concentrated on sparse view for parallel beam due to the central slice theorem which directly derived from parallel beam geometry.
For Fourier-based fan reconstruction, the process of rebinning is necessary because of the limit of central slice theorem. In general, because the number of angular sampling is smaller than full scanning, the missing data cannot be interpolated without aliasing.[22] Therefore, the rebinning of fan sparse views is not straightforward suitable, and it needs to combine with other methods.
Inspired by previous work, we aim to present a promising contribution to the task of image reconstruction from fan sparse views in Fourier domain. To conveniently record the rebinning data between Fourier domain and image space, the selective matrix is presented to keep the known data constant. Combining the alternating direction total variation minimization (ADTVM) technique with NUFFT, a new method is proposed which is suitable for large-scale reconstruction because of high computational efficiency of FFT. The advantages of the proposed algorithm are identified based on the results of several group experiments.
This paper is organized as follows. Section 1 briefly reviews the basic CT reconstruction and the current research state of fan sparse-view image reconstruction. Section 2 describes the basic principles of the proposed method, which mainly include a selective matrix and a constrained TV minimization model. Section 3 demonstrates groups of typical experiment results, including numerical and real-data simulations. Finally, Section 4 presents the discussion and conclusion.
In this section, the new method is described in detail, which mainly includes the methods of central slice theorem, fan projection data rebinning, selective matrix, and constrained TV minimization reconstruction via NUFFT.
Central slice theorem (also called projection theorem) is outlined to review the foundation of Fourier reconstruction in the following. The basic geometry is shown in Fig.

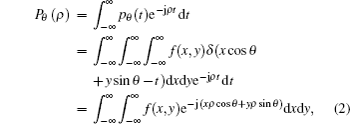

Combined with Eqs. (

Namely, the one-dimensional (1D) FFT Pθ (ρ) of the parallel projection is equal to 2D FFT F (u,v) of reconstruction objection in the direction perpendicular to the projection. In addition, the polar coordinate data cannot be directly transformed to spatial domain by IFFT and it needs transform to Cartesian coordinate which make plenty of streak artifacts due to the introduction of the interpolation. The adjoint of NUFFT can realize reconstruction from polar coordinate data and avoid interpolation form polar coordinate to Cartesian coordinate. Based on the latest NUFFT, we can design the following efficiency reconstruction.
Given the limitation of parallel projection, other imaging geometries, including fan beam imaging geometry, needs a rebinning process before developing Fourier-based reconstruction methods. According to their geometric relationship (see Fig.
From Fig.

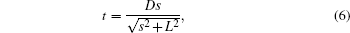
In the background of sparse fan beam view, the process of rebinning is complicated for a small number of projection data. A high number of missing data corresponds to a less precise value after rebinning.
In this work, we introduce selective matrix, which remarks the location of the value after rebinning. In other words, the selective matrix consists of elements 0 and 1, in which the value is 1 when the place is rebinned (these filled dots are shown in Fig. Rebinning to parallel beam projection from sparse fan beam.

The projection can be easily restrained during iterative Fourier-based reconstruction with the establishment of a selective matrix. The introduction of a selective matrix promotes reconstruction by remarking these known positions.
Let f denote the two-dimensional image, then sparse model can be linearly expressed as follows:


The preceding Fourier model can be concisely written as follows by letting Fs = s FN:
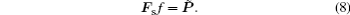
To solve this linear and underdetermined equation, we specify a TV minimization algorithm that considers the reconstruction a task of finding the best solution to the following optimization problem:
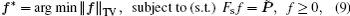


Its corresponding augmented Lagrangian function of Eq. (

Given that equation (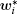

The task of solving Eq. (
Suppose that fk and wi,k, respectively, denote the approximate minimizers at the k-th iteration which refers to the inner iteration, while solving the subproblem. If fj and wi,j are available for all j = 0,1,…,k, then wi,k+1 can be attained by

The w-subproblem is separable with respect to wi, and equation (

In addition, with the aid of wi,k+1, the f-subproblem can be achieved by solving the following equation:

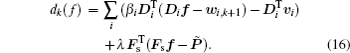
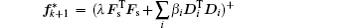

The optimized solution for Eq. (

Thus, all issues in the process of handling the subproblems have been settled in the preceding sections. In light of all the preceding derivations, the new algorithm for fan sparse-view reconstruction is stated as follows.
It is noticeable that this property of iteration mainly depends on alternating direction method. Therefore, the convergence of algorithm is inevitable for the proof convergence of ADM.[27] The Fourier-based algorithm here is validated that the complexity decreases from O(N3) to O(N2logN) for NUFFT and its adjoint. The proposed non-uniform Fourier reconstruction based on TV regularization algorithm for sparse fan projection is called NUTVM in this paper.
We implement the proposed NUTVM in MATLAB environment to demonstrate its excellent performance. It is also evaluated with both digital simulation data and real CT data. All experiments are performed on an HP Z820 workstation with Intel Xeon E5-2620 dual-core CPU (2 GHz) and 24 GB memory.
We perform the simulation studies with a 2D modified Shepp–Logan phantom, which is generated according to the definition of the ellipse phantom image, to validate the performance of our proposed method. Circular equally spaced fan beam geometry is adopted. In the experiment, the detector elements are linearly spaced within the line detector where the size of one pitch is assumed to be 0.127 mm × 0.127 mm. The scanning and reconstruction parameters in the experiment are listed in Table
| Table 1. Parameters in the simulation of a sparse fan scan. . |
To further evaluate the reconstruction results, the root mean square error (RMSE) is introduced, which can be written as
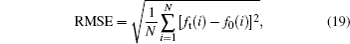
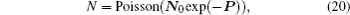
The image was reconstructed with ASD-POCS, ADTVM, and the proposed method, and their results are presented in Fig.
In Fig.
RMSE is used as an evaluation criterion for three different algorithms with iteration time. The result is shown in Fig.
| Table 2. Accuracy and the running time and memory allocation of different methods. . |
From the reconstruction images, the corresponding profiles and RMSE, we can see that there is little difference between the reconstructed image using the NUTVM algorithm and the reference image, which demonstrate the correctness of the proposed algorithm. The reconstruction quality of NUTVM algorithm is an improvement over that of the ASD-POCS algorithm. In terms of reconstruction time, the new method is obviously superior to the other two contrastive algorithms. However, the reconstructed quality worsens for the existence of noise when the iteration number is over a certain number.
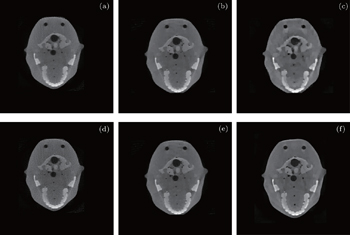
We performed the experiments to reconstruct a slice of the head model from real data to further check the capability of the NUTVM algorithm. The scanning and reconstruction parameters are listed in Table
| Table 3. Parameters in the sparse-view fan scanning. . |
Image reconstructions through ASD-POCS and ADTVM algorithms and the proposed algorithm are shown in Fig.
Then the running time and memory allocation of each reconstruction method are presented in detail in Table
| Table 4. The running time and memory allocation of different methods. . |
The acquired reconstruction results via real data clearly show that the quality of the reconstructed image improved as the number of iterations increased. Under the same number of iterations, the reconstruction results of ADTVM are superior to those of ASD-POCS, particularly in terms of the high-frequency information showing the image detail or volatile part. Compared with ADTVM, the results of the new method are approximate from the view of the image detail.
The simulated data agree well with the theoretical analysis for the 2D Fourier propriety to the reconstructed object. According to the preceding results, we examine the proposed iterative algorithm, which shows potential improvement. During the numerical simulation experiment, we determined that error from rebinning mainly depends on the choice of interpolation. In general, choosing an intricate interpolation method, such as polynomial function, helps in improving the quality of the reconstruction image to full angle scanning. However, the lack of projection data leads to an increased number of errors because the intricate interpolation method must use global data. Thus, excellent results must be realized by a simple interpolation, such as linear interpolation. According to the RMSE curve of the three different algorithms in the numerical simulation, the error stops decreasing when it arrives at the iteration number for the existing noise. This phenomenon is in accordance with the real reconstruction data because of the existing irregular noise. In the experiment, memory allocation by NUTVM is the smallest among the other contrastive algorithms. This preference mainly depends on FFT, encompassing low computation complexity and high computation time.
Due to the lack of sufficient measurements, the reconstruction procedure can be treated as an ill-posed inverse problem for sparse view, which generally has no unique solution. Based on the continuity of piecewise constant, the TV minimization model can uniquely reconstruct object by high probability. However, it is known that transformation between different data domains is the most computationally expensive part of the whole algorithm. Fortunately, NUFFT and adjoint NUFFT tackle with the transform, which makes this algorithm highly computationally efficient. In addition, unlike ART-based algorithms, the new method does not have to model the system matrix and the data consistency can be retained. The proposed method may have a greater capacity for reducing artifacts and reconstructing better quality images.
A chief contribution of this study is the proposal of a new, efficient TV minimization scheme with NUFFT for fan sparse projections. The validity of the proposed algorithm is verified by conducting numerical simulations and real-data experiments. The advantages of NUTVM indicate that the proposed algorithm is a good choice for fast, low-dose reconstruction in fan beam sparse scanning. Furthermore, it has potential in extending to the cone beam reconstruction in the Fourier domain because of fan basic properties.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 |








 While “not achieved maximum iteration loops,” Do
While “not achieved maximum iteration loops,” Do

