Metamaterials, artificial electromagnetic media that are structured on the subwavelength scale, have received considerable attention due to their exotic physical properties that are normally unavailable in nature, such as the negative index of refraction,^[1] the inverse Doppler effect,^[2] and so on. By using these artificial metamaterials with extraordinary properties, researchers can make invisibility cloaks,^[3] perfect lenses,^[4] absorbers^[5,6] or other devices.^[7] The metamaterial-based absorber is an important application of metamaterials. Through designing the physical scale of the structure and orderly arranging it, researchers can develop a metamaterial absorber (MA) with many excellent properties, for example a thin product which is not limited to one-quarter wavelength thickness, and which has high absorption, and is small-sized, etc. The first perfect MA, having the experimental absorptivity of about 88% at microwave frequencies, composed of an electrical ring resonator and a split wire separated by a dielectric layer, was demonstrated by Landy et al.^[8] Since then, the perfect absorbers have attracted considerable interest, and a large number of absorbers have been proposed and demonstrated from microwave to optical frequencies.^[9–12]

As a matter of fact, the development of the perfect MA is especially attractive at terahertz (THz) frequencies where it is not easy to find naturally occurring materials with strong absorption coefficients. Such absorbers could clearly be of use for thermal imaging, thermal bolometry, wavelength selective radiation, stealth technology, and nondestructive detection. A lot of effort has been made to achieve THz metamaterial absorbers with perfect absorption. Tao et al. obtained an absorptivity of 97% at 1.6 THz;^[13] Landy et al. and Grant et al. gained a polarization-insensitive MA, respectively.^[14,15] However, all these efforts shared the common shortcoming of single band absorption, which becomes an obstacle to their practical applications. However, in many cases, such as THz spectroscopic imagers and detectors, an absorber with multiband is required, since the detector based on the multiband absorber can realize frequency selective detection, decrease the environmental disturbance, and consequently increase the detection sensitivity and imaging resolution. One of the effective methods of multiband operation is to use single-layer structure with two or multiple resonators.^[16–21] Following this design strategy, multiband (or broadband) absorbers have been demonstrated in a wide frequency region ranging from microwave to optics,^[22–24] but the same shape resonator will result in significant mutual coupling between several elements when the positions of several metallic patches are close to each other. An alternative method is to use multiple vertically stacked metallic layers to obtain the multiband metamaterial absorbers, each absorption band corresponding to a specific layer.^[25–28] Another approach for making multiple absorber bands is to utilize single-layer dielectric structure with one metallic element constructed of a special geometric shape.^[29,30] However, both of these structures are very complicated, imposing considerable restrictions on both design and fabrication. Although the metamaterial absorbers have been demonstrated effectively to make multiband absorption, the designs are mostly based on the overlapping of the fundamental resonance of the regular single-band absorber. There is little novelty in designing the new types of multiband absorbers.

In comparison to previous designs, the proposed multiband MA in this paper has several important advantages. Most importantly, it is formed by a U-shaped metallic ring and metallic ground plane, separated by a dielectric layer, so the structure is very simple and easy to fabricate. In addition, it presents three absorption peaks in the designed structure and is made on a highly thin-flexible polyimide substrate with a total thickness of 9.4 μm, which can be used in the non-planar case. Moreover, the multiband absorption peaks in our designed metamaterial structure exhibit high sensing sensitivity, which can be used to fabricate multi-wavelength high-sensitive sensors in the THz region.

To achieve a high absorbing efficiency at multiple THz frequencies, a metamaterial THz absorber based on resonator ring structure is designed. The schematic diagrams are shown in Fig. 1. Figure 1(a) shows the top view of the layout of one unit cell of the proposed MA structure. Basically, there is a U-shaped metallic ring. Figure 1(b) shows the cross sectional view of the proposed MA. As can be seen, it consists of three layers: metal/dielectric/metal. The U-shaped ring structure is fabricated in the top metallic film, which is actually an electrical ring resonator. In this way, the proposed MA consists of an electrical ring resonator. By employing this resonator structure, one can achieve a highly efficient absorption in a wide waveband with multiple absorption peaks.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematics of metamaterial-based THz absorber: (a) U-shaped ring structure on the top of a polyimide spacer and one unit cell showing the direction of propagation of incident THz waves, and (b) cross-sectional view of the unit cell. The period (P) of unit cell is P = Px = Py = 27 μm.

By employing the commercial finite-difference time domain (FDTD) software package (Lumerical FDTD solutions), the proposed MA is modeled and analyzed. The three-dimensional simulations are performed by a normally incident plane wave with the electric field parallel to the x axis. Periodic boundary conditions are employed for both x and y directions with a mesh step size of Δx = Δy = 0.25 μm, and a perfect matching layer boundary condition is employed in z direction with a mesh step size of Δz = 0.05 μm. The inset of Fig. 1(a) shows the direction of incident THz waves with respect to the cross section of the designed absorber. Two metallic layers of this MA are modeled as lossy metal gold with a frequency-independent conductivity of 4.09 × 10⁷ S/m. The dielectric layer is modeled as polyimide with n = 1.68+0.06i.^[15] The polyimide is highly flexible and transmission for the terahertz wave.^[31] According to our simulation, the absorption, A, is obtained by A = 1 − T − R, where T = |S₂₁|² (transmission) is suppressed in overall spectral range (T = |S₂₁|² = 0) as the thickness of the ground metallic plane (200 nm) is much larger than its skin depth, then the absorptivity is calculated by A = 1 − R. The A may achieve perfect absorption when the R = |S₁₁| ² (reflection) is close to zero (i.e., impedance matched to the free space).

For impedance matching, the thicknesses of the metal and dielectric layer should be optimized so that the maximum absorption can be achieved. In simulations, the thickness of the top metal t₁ = 200 nm, which has the same thickness as that of the ground metal plane. On the other hand, the thickness of the dielectric film also affects the absorption, because it influences the THz wave interaction between the adjacent metal layers. In the metamaterial THz absorber, the optimal thickness of polyimide layer (t₂) is found to be t₂ = 9 μm. Next, the structural parameters of the U-shaped ring are optimized so that the absorber achieves the highest absorption. The optimized geometric parameters are as follows in micrometers: L₁ = 24, L₂ = 15, L₃ = 5, W₁ = 9, W₂ = 6, W₃ = 9, and W₄ = 2. These parameters are chosen in microscale so that the microstructure can be realized by the normal photolithography technology.

The simulated results of the S-parameters and absorption spectra of the proposed MA are shown in Fig. 2(a), from which we observe three discrete absorption peaks at frequencies of 1.50 THz (f₁), 3.33 THz (f₂), and 5.40 THz (f₃), with absorptivities of 99.15%, 99.76%, and 99.85%, respectively. The absorption bandwidths, defined as the strict criterion of absorptivity of >80%, are 0.37 THz, 0.34 THz, and 0.58 THz for modes f₁, f₂, and f₃, respectively, and the off-resonance absorption is very small. These simulated results indicate a strong frequency selectivity of the proposed MA due to the narrow absorption bandwidth.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Absorption spectra of the proposed MA. Distributions of the electric field [real(Ez)] in the top plane of the U-shaped metallic loop at frequencies of 1.50 THz (b), 3.33 THz (c), and 5.40 THz (d), respectively, for the x-polarization illumination.

To understand the physical origin of the absorption peaks, we give the simulated normal components of electric field (E_z, in the top plane of the U-shaped metallic ring) distributions corresponding to the above mentioned three resonance frequencies (f₁, f₂, f₃) in Figs. 2(b)–2(d). The electric field E_z distribution in Fig. 2(b) shows the excitation of the fundamental dipole corresponding to opposite charges accumulating at the arms of the U-shaped metallic ring. The higher-order modes occur at THz frequencies due to the fact that the ring perimeter is larger than a multiple of a half-wavelength of the modes. From the field map at f₂ (3.33 THz), we note that the electric field E_z distribution shows excitation of multiple half wavelength charge oscillations in the U-shaped metallic ring corresponding to the second-order mode as shown in Fig. 2(c). Similarly, the third major peak at f₃ (5.40 THz) in the absorption spectra arises due to the third-order excitation of multiple half wavelength charge oscillations in the top plane of the U-shaped metallic ring as shown in Fig. 2(d).

According to our theoretical simulations, different order resonance absorption frequencies can be excited from the external THz field by the model of standing-wave plasmonic resonances. Under the electromagnetic wave illumination, the oscillation of the electrons within the metal film will be driven by the electrical field of the incident THz radiations to form localized surface plasmon; thus, positive and negative surface charges will be alternately accumulated at both sides of the edges of the U-shaped ring. Moreover, these electrons oscillating around the U-shaped ring form a kind of standing wave surrounding the ring. The lengths of the antinodes of the standing waves are mainly determined by the average perimeter of the ring, which explains why the frequencies of the resonance absorption peaks are perimeter related. In this case, the resonance responses of the absorber mainly depend on their average perimeter so that their characteristic resonance frequencies can be determined by the standing-wave model.^[32] The frequency of the absorber is given by

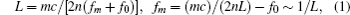
To further understand the THz absorption behavior of the proposed MA, we also analyze the electric field |E| distribution in the structure. Figures 3(a)–3(c) show the electric field intensity profiles in the x–y plane at the air-ring spacer interface for the MA at the three resonance frequencies f₁, f₂, and f₃, respectively. The electric field is localized at the inner edges, outer edges, and corners of the ring structure. The field localization is further confirmed when we see the electric field profiles along the x–z plane as shown in Figs. 3(d)–3(f). These field localizations indicate that localized surface plasmons are excited at these frequencies. For non-magnetic materials, the absorbed electromagnetic power can be calculated by a simple formula P_abs = (1/2)ωɛ″|E|², where ω is the angular frequency, ɛ″ is the imaginary part of the permittivity, and |E| is the amplitude of the total electric field within the material. As a result, the loss caused by localized surface plasmon resonances in the metal structures is large enough to show high absorption.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The electric field (|E|) in the MA structure with a 9-μm thick polyimide spacer and x–z plane at y = 0 μm at frequencies of 1.50 THz (a) and (d), 3.33 THz (b) and (e), and 5.40 THz (c) and (f).

In addition, the simulated power absorption distributions for the U-shaped metallic ring are shown in Figs. 4(a)–4(c), while a cross section of the power distribution in x–z plane at y = 0 μm is shown in Figs. 4(d)–4(f). From these plots, it is clear that the majority of the energy is dissipated as ohmic loss in the U-shaped metallic ring layer and as dielectric loss in the first 500 nm of polyimide below this layer. The regions of maximum absorption loss mainly occur around the outer and inner edges of the U-shaped metallic ring.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Energy dissipation in the MA structure with a 9-μm-thick polyimide spacer and x–z plane at y = 0 μm at frequencies of 1.50 THz (a) and (d), 3.33 THz (b) and (e), and 5.40 THz (c) and (f).

Furthermore, the simulated results for different incident polarization angles of the THz wave are shown in Fig. 5(a). As shown in the figure, the absorption peaks (f₁ and f₃) have a slight shift with the increase of incidence polarization angle due to the asymmetry of structure. However, the two absorption peaks still remain more than absorptivities of 99% for different incident polarization angles. For the second absorption peak (f₂), we observe that the incident polarization angle has great impact on the absorption intensity. Moreover, the frequency of the absorption peak can be switched gradually from 3.33 to 2.71 THz when the incident polarization angle increases from 0° (E ‖ x-axis) to 90° (E ‖ y-axis), which is indicated by two vertical arrows. When the incident polarization angle increases from 0° to 90°, the absorptivity of the second absorption peak drops significantly to 46.7%, and the absorption intensity modulation depth, which is defined as (I_max − I_min)/I_max, is 53.3%. The absorptivity of the new absorption peak (2.71 THz) can increase from 22.4% for incident polarization angle of 0° to 94.8% for incident polarization angle of 90°, and the absorption intensity modulation depth is 76.4%. The resonance absorption peaks of 2.71 and 3.33 THz merged with each other to form a broader absorption band as shown in 53° polarization, and the bandwidth is 1.03 THz for the absorptivity beyond 60%. In addition, the variations of peak absorptivities as functions of incident polarization angle are shown in Fig. 5(b). It is worth noticing that when the incident polarization angle changes from 0° to 180°, the absorptivity for 3.33 THz behaves like a sine function of incident polarization angle and for 2.71 THz, it behaves like a cosine function. This characteristic makes such a structure applicable as a polarization-dependent reflection or absorption switch. We could switch its resonance between 2.71 THz and 3.33 THz by rotating around the z axis.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) Absorption spectra for different incident polarization angles of 0°, 30°, 45°, 53°, 60°, and 90°. (b) Maximum absorptivity as a function of the incident polarization angle for 2.71 THz and 3.33 THz, respectively.

Fabrication errors cannot be avoided because the optimum design of the proposed MA cannot be perfectly fabricated in reality. To evaluate the effect of the fabrication errors on absorption, we take errors for three parameters: thickness of the dielectric layer (t₂), the period (P), and the arm width (W₄) of the U-shaped ring.

Here, we first discuss the effect of the dielectric layer thickness t₂ on the absorption spectra. Figure 6(a) shows the absorption spectra with the size of t₂ changed from 7 μm to 11 μm. From the picture, it can be found that the change of t₂ has different effects on different absorption peaks. For the first and second absorption peaks, when changing the parameter t₂ from 7 μm to 11 μm, the two absorption peaks still remain greater than 99%, and the resonance frequency shows a slight red-shift which drifts to lower frequency. For the third absorption peak, when increasing the dielectric layer thickness t₂ from 7 μm to 11 μm, the absorption peak increases from 98.03% to 99.99%, and the resonance frequency shows a slight blue-shift.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Absorption spectra of metamaterial absorber for the incident polarization angle of 0° at different parameters errors. (a) Absorption spectra in different dielectric thicknesses. (b) Absorption spectra with different linewidths. (c) Absorption spectra of unit cells with different periods.

Next, we discuss the effect of the arm width W₄ on the absorption spectra. Figure 6(b) shows the absorption spectra with the size of W₄ changed from 1 μm to 3 μm. From the picture, it can be seen that the three resonance frequencies drift to higher frequency. The three absorption peaks decrease, but they still remain greater than 98% when changing the parameter W₄ from 1 μm to 3 μm.

Furthermore, we discuss the effect of the period P on the absorption spectra. Figure 6(c) shows the absorption with the size of P changed from 25 μm to 33 μm. From the picture, we can see that the period P has little effect on both the first and second absorption peaks but has a large influence on the resonance frequency. On the contrary, the third resonance frequency and absorption peak are sensitive to period P. As the size of the period P increases, the third absorption peak decreases sharply and the resonance frequency has an obvious red-shift. Therefore, in order to make sure all three absorption peaks are greater than 99%, the period P should be no more than 30 μm.

Based on the above analysis, we can see that only the parameter P has a large influence on absorptivities of the absorption peaks. This is an advantage for the mask fabrication because less processing accuracy is required to fabricate the structure of the proposed MA.

We next investigate the refraction index (RI) sensing of the proposed MA when the RI of the analyte changes but the thickness stays constant, as shown in Fig. 7(a). When the RI is varied from 1.0 (vacuum) to 1.5 in intervals of 0.1, it is obvious that the frequency change for mode f₁ is nearly absent, while obvious red-shifts of the modes f₂ and f₃ are observed. The total frequency shift of the mode f₁ by changing the RI of the analyte from n = 1.0 to n = 1.5 is found to be about 0.211 THz. However, the total frequency shifts of the modes f₂ and f₃ are 0.422 THz and 0.633 THz at the same condition, respectively. Figure 7(b) shows the frequency shifts of the three modes when the RI changes from 1.0 to 1.5 with 0.1 steps. The red, blue, and magenta lines are the linear fits of the three sets of data, respectively.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (a) The transmission spectra of the proposed MA with 10-μm-thick analyte overlays, the RIs of the analyte are 1, 1.1, 1.2, 1.3, 1.4, and 1.5, respectively. (b) The redshifts of the three modes (f1, f2, and f3) versus the RI of the analyte.

From Fig. 7(b), we can see that the frequency shifts of the three resonance modes are almost linear with the increase of RI. To evaluate the sensitivity of the proposed MA, we define S_RI = δf/δn, where δ f is the frequency shift and δ n is the RI variation. The expression represents the resolution of resonance frequency per refractive index unit (RIU). For the analyte coating, the sensitivities of three resonance modes are 0.422, 0.844, and 1.266 THz/RIU, respectively. We convert these numbers into Δλ /RIU by using , where c is the speed of light, f₀ is the resonance frequency, and n represents the RI of the analyte. In terms of Δλ/RIU, the corresponding sensitivities that we obtain for the analyte coating with modes f₁, f₂, and f₃ are 5.76 × 10⁴, 2.29 × 10⁴, and 1.30 × 10⁴ nm/RIU, respectively. Our results show that the proposed MA structure can be used for the multi-wavelength high sensitivity sensing in the THz region.

In summary, we have designed a highly efficient THz multiband metamaterial absorber. Depending on the incident wave polarization, the absorber exhibits multifunctional application such as three-band, four-band, and broadband absorptions, which is useful in dynamically tuning the response of the absorber. In particular, the proposed MA can switch a narrow absorption band from 2.71 THz to 3.33 THz by rotating the device relative to the polarization direction from 90° to 0°. The high absorptivity of the proposed MA can be explained by the effect of the multipolar localized surface plasmon resonance enhancement. The error analyses of different structural parameters show that the error of the period has a great effect on the absorbing performance but the other two parameters have a slight effect. The proposed MA exhibits high refractive-index sensing sensitivity, which has potential applications in multi-wavelength sensing at THz frequencies.