† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11074179 and 10747007), the National Basic Research Program of China (Grant No. 2014CB643702), the Zhejiang Provincial Natural Science Foundation of China (Grant No. LY14E010006), the Construction Plan for Scientific Research Innovation Teams of Universities in Sichuan Province, China (Grant No. 12TD008), the Scientific Research Foundation for the Returned Overseas Chinese Scholars of the Education Ministry, China, and the Program for Key Science and Technology Innovation Team of Zhejiang Province, China (Grant No. 2013TD08).
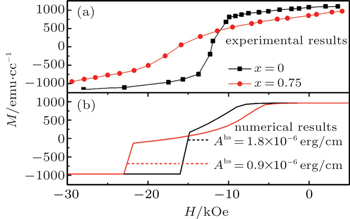
The hysteresis loops as well as the spin distributions of Sm–Co/α-Fe bilayers have been investigated by both three-dimensional (3D) and one-dimensional (1D) micromagnetic calculations, focusing on the effect of the interface exchange coupling under various soft layer thicknesses ts. The exchange coupling coefficient Ahs between the hard and soft layers varies from 1.8 × 10−6 erg/cm to 0.45 × 10−6 erg/cm, while the soft layer thickness increases from 2 nm to 10 nm. As the exchange coupling decreases, the squareness of the loop gradually deteriorates, both pinning and coercive fields rise up monotonically, and the nucleation field goes down. On the other hand, an increment of the soft layer thickness leads to a significant drop of the nucleation field, the deterioration of the hysteresis loop squareness, and an increase of the remanence. The simulated loops based on the 3D and 1D methods are consistent with each other and in good agreement with the measured loops for Sm–Co/α-Fe multilayers.
Since an exchange-coupled composite material was proposed by Kneller in 1991,[1] with a hard phase to provide high coercivity and a soft phase to provide high saturation and remanence, the coercivity, structural, and magnetic properties in permanent magnets have always been an important topic in magnetism.[2–4] An energy product paradox was proposed in some literatures, which has been intensively studied in both experimental[5–8] and theoretical[9–15] works by condensed matter physicists. A lot of works have been devoted to the exploration of the largest energy product experimentally reachable. In 1993, Skomski et al.[16] proposed that the theoretical energy product (BH)max of oriented composite magnets could be as large as 120 MG·Oe, which almost doubled that of the best available single-phase permanent magnets.
In order to realize such a giant energy product, many scientists have done a lot of work in the past two decades. A close review shows that the experimental remanence is close to the predicted one, however, the measured coercivity is much smaller.[17–20] Therefore, such an energy product paradox is intrinsically linked to Brown’s coercivity paradox, i.e., the measured coercivity is much smaller than that predicted by the available theory. Experimentally, huge progresses have been made recently: an energy product (BH)max of 60 MG·Oe has been obtained in Nd–Fe–B/Fe–Co multilayers by Cui et al.,[5] while a value of 40 MG·Oe has been reached by Sawatzki et al. in SmCo5/Fe/SmCo5.[21] It is worth noting that at high temperature, the magnetic properties of Nd–Fe–B are inferior to those of Sm–Co due to a lower Curie temperature (about 400 °C against 800 °C), which can occasionally make Sm–Co a better choice compared to Nd–Fe–B.
In the pursuit of the highest energy product reachable, a new structure has been discovered and investigated: the inclusion of an interface layer within bilayers. Choi et al.[22] found that the maximum energy product of Sm–Co/α-Fe bilayers can be improved by 50% with an intermixed interface layer, and reach a value of 15 MG·Oe. Zhang et al.[23–25] discovered that by inserting thin non-magnetic spacer layers like Cu in SmCo5/Fe, increased coercivity and pinning fields can be realized. As a result, (BH)max jumps from 9 MG·Oe to 32 MG·Oe with a coercivity of 7.24 kOe. The single-phase behavior and the irreversible rotation in the demagnetization process indicates a strong exchange coupling between the Sm(Co, Cu)5 and Fe layers. Moreover, Liu et al.[26] discovered that the Fe/Co mixture behavior enhances the interface exchange-coupling and improves the remanence as well as the coercivity of the composite magnet.
In a word, the interface exchange coupling is important in realizing good magnetic properties in Sm–Co/α-Fe layered systems, which, however, have seldom been investigated systematically in theory. In this paper, three-dimensional (3D) micromagnetic simulations and analytical calculations are performed for Sm–Co/α-Fe bilayers, which are then compared to our experimental results. This work focuses on the influence of the exchange coupling and the soft phase thickness on the coercivity and nucleation fields of the system.
Our calculation is based on an exchange-coupled bilayer (see Fig.
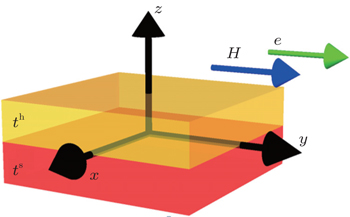 | Fig. 1. Basic scheme of the investigated hard/soft bilayers in the three-dimensional micromagnetic model. |
The 3D micromagnetic calculation of the software OOMMF is based on the Landau–Lishitz–Gilbert dynamic equation[27]
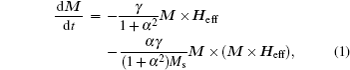
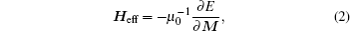
In the 3D simulations, the system is set as a tetragonal box of sizes 300 nm×300 nm×t. The variable t is the thickness of the layers, namely, t = th + ts, as shown in Fig.
In this paper, Sm–Co is chosen as the hard layer, while α-Fe is the soft layer. The material parameters used in the simulation are: Ms = 1.71 × 103 emu/cc, Mh = 5.5 × 102 emu/cc, Ks = 4.6 × 105 erg/cc, Kh = 5 × 107 erg/cc, As = 2.5 × 10−6 erg/cm, and Ah = 1.2 × 10−6 erg/cm, which are adopted from Refs. [15], [29], and [30]. Here, A, K, and M denote the exchange energy constant, the anisotropy constant, and the spontaneous magnetization, respectively. Only the exchange interaction between the neighboring region pair is taken into account and the free boundary conditions are chosen. The interface coupling is difficult to describe precisely, as it depends not only on the bulk crystalline structures of the hard and soft layers, but also on the strength of the interface exchange coupling. The exchange energy constant between the soft and hard layers Ahs is set as 1.8 × 10−6 erg/cm when Sm–Co/α-Fe is in full coupling, while it is taken as 0.9 × 10−6 erg/cm and 0.45 × 10−6 erg/cm for low coupling.
The analytical calculation is carried out supposing all layers extending to infinity, which is referred to as the 1D method. The magnetization can be calculated as a function of z, given that the magnetization is uniform within the layer plane (xy plane). The energy density per area in the film plane is[15,29,31,32]
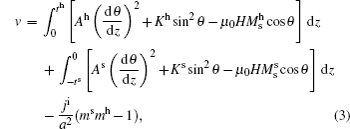
By applying the variational method to the interface exchange coupling energy with suitable boundary conditions, we obtain
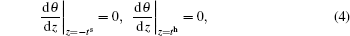
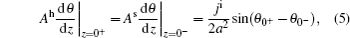
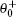
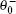
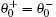
In particular, at the nucleation state, the deviation of the magnetization from the applied field direction is small. Thus, the nucleation problem can be solved by an appropriate ansatz or series expansion[14]
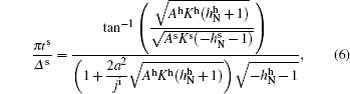
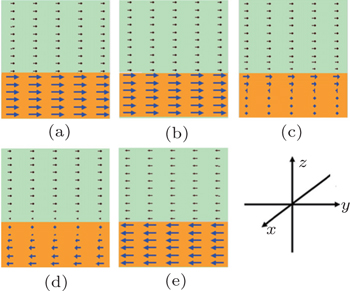
Figure
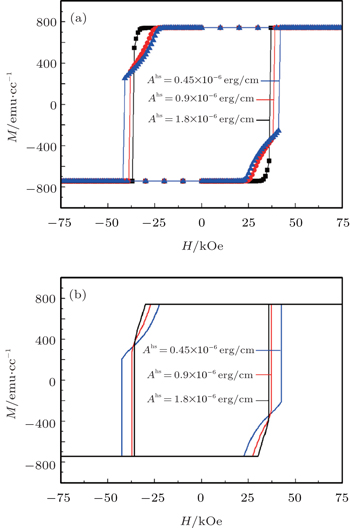 | Fig. 2. Macroscopic hysteresis loops of Sm–Co(10 nm)/α-Fe(2 nm) bilayers obtained by (a) 3D simulations and (b) analytical calculations. |
When Sm–Co/α-Fe has an exchange coupling of Ahs = 1.8 × 10−6 erg/cm, the shape of the hysteresis loop is essentially a rectangle according to the 3D simulations, where the nucleation and pinning fields are close to each other. When Ahs decreases from 1.8 × 10−6 erg/cm to 4.5 × 10−7 erg/cm, the gap between nucleation and pinning fields rises from 3.5 kOe to 21 kOe. On the other hand, there is an obvious nucleation point at the applied field of −29.6 kOe for Ahs = 1.8 × 10−6 erg/cm according to the 1D calculation, which is quite different from the corresponding pinning point at H = −35.8 kOe. This gap between the nucleation and pinning fields rises to 20 kOe as Ahs decreases to 4.5 × 10−7 erg/cm.
| Table 1. Calculated magnetic properties of Sm–Co/α -Fe based on the OOMMF software and 1D calculation, where th = 10 nm. . |
As shown in the previous studies,[13–15,29] the hysteresis loop and the coercivity mechanism are sensitive to the soft layer thickness. Zhao et al. found that as the soft layer thickness increases, the coercivity mechanism changes from nucleation to pinning when the hard layer is large enough. Besides, Asti et al. found that the magnetic phase diagram changes from rigid composite magnet to exchange-spring and finally to decoupled magnet with the increase of the soft layer thickness. Therefore, the hysteresis loops are calculated for various Ahs with ts = 6 nm, as shown in Fig.
 | Fig. 3. Macroscopic hysteresis loops of Sm–Co(10 nm)/α-Fe(6 nm) bilayers obtained by (a) 3D simulations and (b) analytical calculations. |
Figure
Experimentally, the interface of the hard/soft layers has been intensively modified to obtain the best performance for the exchange spring film. A spacing layer Ta was inserted between Nd2Fe14B and FeCo layers to adjust the exchange coupling and magnetostatic interaction to obtain the largest (BH)max in NdFeB-based nanocompiste films.[5] For the SmCo/Fe system, a diffusion layer was reported to be effective for getting a larger nucleation field and hence (BH)max.[6] A Cu layer was used in multilayer films Cr(50 nm)/[SmCo6(9 nm)/Cu(x nm)/Fe(5 nm)/Cu(x nm)]6/Cr(100 nm)/SiO2 (x = 0–0.75) and a high (BH)max of 32 MG·Oe was obtained by some of us.[23–25] Although the Cu layer promotes the crystallization of the SmCo phase to form a uniform multilayer, the Cu layer with different thickness is considered to adjust the exchange coupling as well. In the case of the SmCo layer directly contacting the Fe layer, the exchange coupling is strong. With the Cu thickness increased, the soft and hard phases are separated by the Cu layer, which results in a decrease of the exchange coupling. Figure
Figure
As shown in Fig.
From the above discussion, one can find that a large nucleation field is essential to keep the squareness of the corresponding hysteresis loop. In this section, the dependence of this critical field on the exchange interaction and the soft layer thickness is discussed. In nanocomposite films, the hard phase offers a high anisotropy to produce the high coercivity, but this effect strongly depends on its thickness. If th is smaller than the corresponding Bloch wall width,[14,30] which is about 4.9 nm for Sm–Co, its magnetization will be easily reversed by the soft phase through the exchange interaction. While if th is large enough, the magnetic properties will not depend on it.[33] Therefore, in the calculation below, the thickness of the hard phase is set to 10 nm, which is larger than the Bloch wall width.
Figure
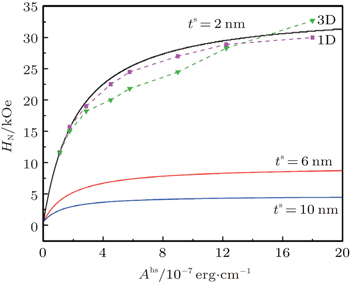 | Fig. 7. Calculated nucleation field as a function of the exchange coupling Ahs. The solid lines are obtained with Eq. ( |
The nucleation field as a function of the thickness of the α-Fe layer under various exchange interactions Ahs is shown in Fig.
The effects of the exchange coupling on magnetic properties were investigated for Sm–Co/α-Fe bilayers using a 3D micromagnetic software OOMMF and a 1D analytical model. A reduced exchange coupling results in lower nucleation fields and higher coercivities. Both methods show agreeable results with the experimental multilayer data. On the other hand, when the soft layer thickness increases, both pinning field and remanence increase whereas the nucleation and coercive fields decrease, leading to the deterioration of the squareness of the loops. The calculated results can partially explain Brown’s coercivity paradox in hard/soft composite materials. A strong exchange coupling is essential to keep the squareness, therefore a large energy product.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 |