Cite this Article
San Xiao-Jiao, Han Bai, Zhao Jing-Geng. Theoretical investigation of structural and optical properties of semi-fluorinated bilayer graphene. Chinese Physics B, 2016, 25(3): 037305  
Permissions
Theoretical investigation of structural and optical properties of semi-fluorinated bilayer graphene
San Xiao-Jiao1, †, , Han Bai2, 3, Zhao Jing-Geng1
Natural Science Research Center, Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150080, China
Key Laboratory of Engineering Dielectrics and Its Application, Ministry of Education, Harbin University of Science and Technology, Harbin 150080, China
College of Electrical & Electronic Engineer, Harbin 150080, China

 

† Corresponding author. E-mail: sanxj@hit.edu.cn

Project supported by the Program of Educational Commission of Heilongjiang Province, China (Grant No. 12541131).

Abstract
Abstract

We have studied the structural and optical properties of semi-fluorinated bilayer graphene using density functional theory. When the interlayer distance is 1.62 Å, the two graphene layers in AA stacking can form strong chemical bonds. Under an in-plane stress of 6.8 GPa, this semi-fluorinated bilayer graphene becomes the energy minimum. Our calculations indicate that the semi-fluorinated bilayer graphene with the AA stacking sequence and rectangular fluorinated configuration is a nonmagnetic semiconductor (direct gap of 3.46 eV). The electronic behavior at the vicinity of the Fermi level is mainly contributed by the p electrons of carbon atoms forming C=C double bonds. We compare the optical properties of the semi-fluorinated bilayer graphene with those of bilayer graphene stacked in the AA sequence and find that the semi-fluorinated bilayer graphene is anisotropic for the polarization vector on the basal plane of graphene and a red shift occurs in the [010] polarization, which makes the peak at the low-frequency region located within visible light. This investigation is useful to design polarization-dependence optoelectronic devices.

PACS: 73.22.Pr;78.67.Wj;63.22.Rc;71.15.Mb;
Keyword:bilayer graphene;fluorinated configuration;optical properties;density functional theory;
1. Introduction

The first experimentally obtained stable atomic monolayer material is graphene.[1,2] Due to its promising electronic mobility, robustness, and high crystal quality,[3–5] graphene has attracted a great deal of attention. However, its semimetallic nature is problematic with regard to developing usable graphene transistors and devices. Although there are abundant investigations on tailoring the material’s electronic properties in experiment and theory,[6–23] this field remains a major challenge. One alternative solution is to move to the multilayer derivatives.[6–9,24–27] For example, bilayer graphene has a gap tunable via chemical doping or by applying an external gate voltage.[24] Another method for changing the electronic properties of the material is via chemical functionalization of radicals, such as hydrogen,[12–17] oxygen,[18–21] and fluorine atoms,[28–34] which rehybridizes the C atoms from sp2 to sp3. Zhou et al. first investigated semi-hydrogenated graphene labeled graphone with a triangular hydrogenated configuration.[35,36] Their calculations indicated the ferromagnetism and a smaller band gap of ∼ 0.67 eV in this configuration.[36] As for the bilayer graphone, unlike the graphone sheet, the system is nonmagnetic but remains metallic.[27] Using geometry optimization, Feng and Zhang found the stable structure of semi-hydrogenated graphene with a rectangular hydrogenated configuration. The rectangular graphone is antiferromagnetic and has an indirect band gap of ∼ 2.45 eV.[17]

Furthermore, recent studies indeed clarified that bilayer graphene is also an interesting material on its own. Bilayer graphene exists in two stacking modifications, the AB stacking and AA stacking. Previously, most efforts have focused on the AB stacked bilayer graphene. Since 2009, the experimental realization of the AA-stacked graphene has been reported,[37,38] very limited theoretical investigations were focused on the AA-stacked bilayer graphene (AA-BLG).[38–42] The advantage of the AA-stacked graphene is the honeycomb pattern favorable for electron traffic, which is similar to that of an isolated graphene layer. An important feature of the AA-BLG is that the hole and electron Fermi surfaces coincide in the undoped material and such a band structure is unstable. The freestanding AA-BLG is a semiconductor with an indirect band gap of 0.91 eV.[41,42] Our interest on functionalized AA-BLG is driven to extend the family of graphene-based materials and to create materials with a direct band gap in the electronic band structure, which could be applied in electronics, optoelectronics, etc. As for the optoelectronics, the material is better with a direct or quasidirect band gap. To engineer the structural and electronic properties of the AA-BLG, we can dope it with appropriate dopants, choose the substrate, and apply a gate voltage, or apply a combination of these methods.[40] We have found another polymorphic form of one semi-fluorinated graphene and one unfluorinated graphene layer stacked in the AA sequence, where carbon atoms located in top positions and the two layers establish strong covalent bonds with a distance of about 1.62 Å. The semi-fluorinated graphene layer has a rectangular fluorinated configuration. The unfluorinated graphene layer forms double bonds (1.35 Å). The semi-fluorinated bilayer graphene is a wide gap semiconductor with a 3.46 eV direct band gap. Furthermore, the optical properties are calculated and the results indicate that the semi-fluorinated bilayer graphene is anisotropic for the polarization vector on the graphene plane and with the peak at the low-frequency region located within visible light in [010] polarization. The anisotropic features are unexpected in other graphene-related systems, such as graphite, graphene, and bilayer graphene. This investigation is useful to design polarization-dependence optoelectronic applications.

2. Computational details

In order to investigate the structural and optical properties of semi-fluorinated bilayer graphene, we have carried out the following calculations. In the calculation of geometry relaxation and optical properties, density functional theory (DFT) calculations are performed with the CASTEP code[43] using the general gradient approximation[44] (GGA), Perdew–Burke–Ernzerholf (PBE) exchange correlation functional, and norm-conserving pseudopotential. In order to eliminate the interactions between graphene sheets, the vacuum space is set as 25 Å along the direction perpendicular to the carbon plane. The 8×8×1 k-points in the reciprocal space following the Monkhorst–Pack scheme are used. The structure is relaxed with a cutoff energy of 940 eV. No symmetry constraints are used. The convergences of energy and force are set as 10−6 eV and 0.01 eV/ Å, respectively. The phonon frequencies are calculated using the linear response technique within the CASTEP code.[43] Molecular dynamics simulations are performed using DFT within GGA[44] with the PBE parametrization as implemented in the DMol3 program.[45] All-electron treatment and double numerical basis including d- and p-polarization functions (DNP) are used. The convergence of energy in the self consistent field is set as 1 × 10−6 Hartree. The thermal stability of semifluorinated bilayer graphene is considered in the NVT ensemble with a Nose–Hoover thermostat at T = 300 K. Because hybrid functional calculations can give a more accurate band gap, the band gap is also calculated by using the Heyd–Scuseria–Ernzerhof 2006 (HSE06) approximation.[46]

3. Results and discussion
3.1. Structural properties and stability

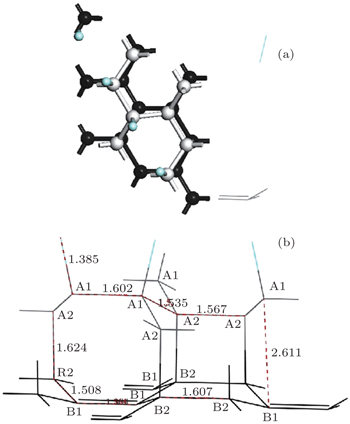
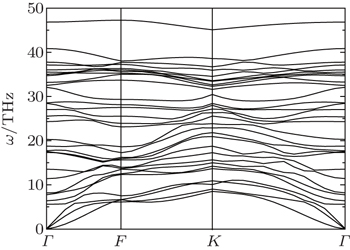
The optimized geometric structure of the semi-fluorinated bilayer graphene stacked in AA sequence is shown in Fig. 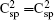1. On the top layer, the fluorinated carbon is labeled A1, the unfluorinated carbon is labeled A2, and the carbons underneath are labeled B1 and B2, respectively. The polymorph obtained in this investigation is with 8×4 membered rings and has a rectangular functionalized configuration. The semi-fluorinated graphene layer and the graphene layer undergo a reconstruction with A2 and B2 carbon atoms forming a covalent bond. The distance between the two graphene layers is about 1.62 Å, which is longer than that in freestanding AA-BLG (1.56 Å).[41] The bond length between F and A1 atom is about 1.39 Å, while the intralayer bond lengths of A1–A1, A1–A2, A2–A2, B1–B2, and B2–B2 are about 1.60 Å, 1.54 Å, 1.57 Å, 1.51 Å, and 1.61 Å, respectively. The remaining B1 carbon atoms form a double bond and the bond length is about 1.36 Å. The angles between adjacent C–C bonds are ∠A1A1A2 = 113.83°, ∠A1A2A1 = 110.94°, ∠A1A2B2 = 112.94°, ∠A2B2B1 = 104.85°, ∠B2B1B1 = 118.82°, and ∠B2B1B2 = 114.30°, while the angles between adjacent C–F and C–C bonds are ∠FA1A1 = 101.97° and ∠FA1A2 = 107.29°. The distance between A1 and A2 two carbon planes is about 0.61 Å, while that between B1 and B2 is about 0.38 Å.

Fig. 1. (a) Top and (b) side views of the semi-fluorinated bilayer graphene in AA configuration. Carbon atoms on top and bottom layers are colored with gray and black, respectively. Fluorine atoms are colored with blue.

To confirm the dynamical stability of the semi-fluorinated bilayer graphene stacked in AA sequence, the phonon dispersion curves have been calculated (Fig. 2). There are no imaginary frequencies observed throughout the whole Brillioun zone, indicating that this compound is dynamically stable.

Fig. 2. Phonon dispersion in the semi-fluorinated bilayer graphene.

Furthermore, molecular dynamics simulations have been performed, applying the same method and parameter settings with Ref. [27]. The fluctuations of the temperature and potential energy in the semi-fluorinated bilayer graphene with AA configuration are plotted in Fig. 3. The compound suffers a slight distortion after 3 ps with the time step of 1 fs, but after full geometry relaxation again, it can be re-optimized back to the previous static structure. It indicates that the compound stacked in AA sequence can also be maintained at room temperature. We also investigate the stability of the semi-hydrogenated bilayer graphene with 8×4 membered rings in AA configuration and compare it to the case of the compound with 7×5 membered rings in AB configuration predicted by Zhou et al.[27] The results indicate that our semi-hydrogenated bilayer graphene has lower energy than that in Ref. [27]. At room temperature, the equilibrium energy of our AA configuration is about −16631.78 eV, while that of the AB configuration is about −16627.69 eV in Ref. [27]. The large energy difference (about 4.1 eV) is mainly due to the different hydrogenated sites, comparable to the case in monolayer graphene, the energy difference between triangular and rectangular configurations being about 3.44 and 2.95 eV per cell comprising eight carbon atoms in our calculations for semi-hydrogenated and semi-fluorinated, respectively.

Fig. 3. Fluctuations of (a) temperature and (b) potential energy in the semi-fluorinated bilayer graphene as a function of time (step 1 fs) during MD simulation.

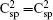
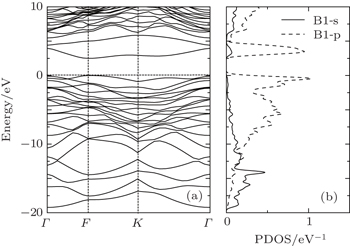The optimized lattice parameters of the semi-fluorinated bilayer graphene are a = b = 5.10 Å. The semi-fluorinated bilayer graphene is a semiconductor with a 2.50 eV direct energy gap at the F point at the PBE level of theory as shown in Fig. 4, whereas the Heyd–Scuseria–Ernzerhof gap is 3.46 eV, which is more accurate. The band gap of the AA-BLG (1.25 eV indirect band gap in our calculation) is widened, and the transformation from indirect to direct band is induced by the rectangular fluorination, which is necessary for the practical applications. The top of the valence bands and the bottom of the conduction bands are mainly occupied by the p electrons from B1 atoms forming double bonds.

Fig. 4. (a) Electronic band structure of the semi-fluorinated bilayer graphene together with (b) the partial density of states (PDOS) of carbon atoms (labeled B1) forming double bonds.

When the interlayer distance is 1.62 Å, the two graphene layers in AA stacking can form strong chemical bonds. Under an in-plane stress of 6.8 GPa, this semi-fluorinated bilayer graphene becomes the energy minimum. Therefore, a possible way to induce the proposed semi-fluorinated bilayer configuration would be to apply an in-plane stress, maybe by growing epitaxially graphene layers on some appropriate substrate with enough lattice mismatch, as the case in AA-BLG.[41]

3.2. Optical properties

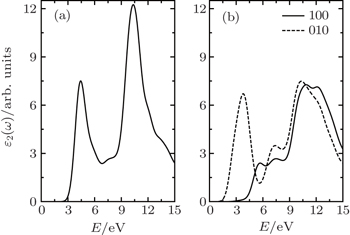The optical properties of the semi-fluorinated bilayer graphene have been calculated and compared with those of the AA-BLG. In our calculations, the intraband contribution to the optical properties is not considered, which mainly affects the low energy infrared part of the spectra. In Fig. 5, the [100] and [010] directions are both on the basal plane of graphene and represent the incident radiations with linear polarizations perpendicular and parallel to the C=C double bonds, respectively.

Fig. 5. Calculated imaginary part of the dielectric function as a function of the photon energy for (a) AA-BLG and (b) semi-fluorinated bilayer graphene.

There are a few good first-principles studies to date on the dielectric constants of 2D materials.[47–49] As mentioned in Ref. [47], quantum confinement is strong at small thickness, which gives rise to a very small ɛ2 in the low-energy range. Overall, the in-plane components (interband transition) of ɛ2 increase with increasing film thickness at all frequencies, conversing towards a constant value, while the general profile of the in-plane interband ɛ2 is consistent. In our calculation, for the dielectric functions ɛ2 presented in this work, we have first multiplied ɛ2 directly from CASTEP calculations by c = 25 Å and then divided it by the nominal film thickness h, where h is 4.95 Å and 5.96 Å for AA-BLG and semi-fluorinated bilayer graphene, respectively (h is the sum of the thickness of graphene (3.35 Å) and the corresponding bulk).

The result of AA-BLG is plotted in Fig. 5(a). In [100] and [010] polarizations, ɛ2(ω) has two peaks at about 4.5 eV and 10.5 eV, implying that AA-BLG is isotropic for the polarization vector on the basal plane of graphene. The first main peak of ɛ2(ω) located at 4.5 eV is weaker than the second main peak at about 10.5 eV. In the case of semi-fluorinated bilayer graphene shown in Fig. 5(b), in the [100] polarization, there is only one prominent peak around 10.5 eV and with two shoulders below it, while in the [010] polarization, there are two main peaks at about 3.0 eV and 10.5 eV and with one shoulder below the latter, implying that the semi-fluorinated bilayer graphene is anisotropic for the polarization vector on the basal plane of graphene. The intensity of the peak around 10.5 eV in both two polarizations decreases largely, which makes the two peaks of ɛ2(ω) located around 3.0 eV and 10.5 eV become comparable. The ɛ2(ω) has a red shift in the [010] polarization, which makes the peak at the low-frequency region located within the visible light.

4. Conclusion

In this work, the structural and optical properties of the semi-fluorinated bilayer graphene have been investigated. Our calculations indicate that the semi-fluorinated bilayer graphene with AA stacking sequence and rectangular fluorinated configuration is dynamically stable and can be maintained at room temperature. When the interlayer distance is 1.62 Å, the chemical bonding occurs, the system is formed by 8×4 membered rings. Under an in-plane stress of 6.8 GPa, this semi-fluorinated bilayer graphene becomes the energy minimum. The semi-fluorinated bilayer graphene is a semiconductor with a 3.46 eV direct band gap at the F point. The p electrons from the B1 atoms are mainly responsible for the electronic behavior at the vicinity of the Fermi level. Furthermore, the semi-fluorinated bilayer graphene is anisotropic and has a peak at the low-frequency region located within visible light in the [010] polarization.

Reference
1Novoselov K SGeim A KMorozov A KJiang DZhang YDubonos S VGrigorieva I VFirsov A A 2004 Science 306 666
2Novoselov K SJiang DSchedin FBooth T JKhotkevich V VMorozov S VGeim A K 2005 Proc. Natl. Acad. Sci. USA 102 10451
3Geim A KNovoselov K S 2007 Nat. Mater. 6 183
4Avouris PChen ZPerebeinos V 2007 Nat. Nanotechnol. 2 605
5Geim A K 2009 Science 324 1530
6Zhao YTang T TGirit CZhao HMartin M CZettl ACrommie M FShen Y RWang F 2009 Nature 459 820
7Castro E VNovoselov K SMorozov S VPeres N M RSantos J DosNilsson JGuinea FGeim A KNeto A H C 2007 Phys. Rev. Lett. 99 216802
8Ribeiro R MPeres N M RCoutinho JBriddon P R 2008 Phys. Rev. B 78 075442
9Boukhvalov D WKatsnelson M I 2008 Phys. Rev. B 78 085413
10Zanella IGuerini SFagan S BMendes JSouza A G 2008 Phys. Rev. B 77 073404
11Gui GLi JZhong J X 2008 Phys. Rev. B 78 075435
12Boukhvalov D WKatsnelson M ILichtenstein A I 2008 Phys. Rev. B 77 035427
13Sofo J OChaudhari A SBarber G D 2007 Phys. Rev. B 75 153401
14Lebegue SKlintenberg MEriksson OKatsnelson M I 2009 Phys. Rev. B 79 245117
15Elias D CNair R RMohiuddin T M GMorozov S VBlake PHalsall M PFerrari A CBoukhvalov D WKatsnelson M IGeim A KNovoselov K S 2009 Science 323 610
16Gao HWang LZhao JDing FLu J 2011 J. Phys. Chem. C 115 3236
17Feng LZhang W X 2012 AIP Advances 2 042138
18Yan JXian LChou M Y 2009 Phys. Rev. Lett. 103 086802
19Jung IDikin D APiner R DRuoff R S 2008 Nano Lett. 8 4283
20Jeong H KJin M HSo K PLim S CLee Y H 2009 J. Phys. D: Appl. Phys. 42 065418
21Luo ZVora P MMele E JJohnson A T CKikkawa J M 2009 Appl. Phys. Lett. 94 111909
22Lu Y HChen WFeng Y PHe P M 2009 J. Phys. Chem. B 113 2
23Lu NLi Z YYang J L 2009 J. Phys. Chem. C 113 16741
24Samarakoon D KWang X Q 2010 ACS Nano 4 4126
25Hu B 2015 Chin. Phys. B 24 087101
26Worasak PBumned S 2015 Chin. Phys. B 24 048101
27Zhou JWang QSun QLena P 2011 Appl. Phys. Lett. 98 063108
28Yuan S JRösner MSchulz AWehling T OKatsnelson M I 2015 Phys. Rev. Lett. 114 047403
29Nair R RRen WJalil RRiaz IKravets V GBritnell LBlake PSchedin FMayorov A SYuan SKatsnelson MICheng H MStrupinski WBulusheva L GOkotrub A VGrigorieva I VGrigorenko A NNovoselov K SGeim A K 2010 Small 6 2877
30Robinson J TBurgess J SJunkermeier C EBadescu S CReinecke T LPerkins F KZalalutdniov M KBaldwin J WCulbertson J CSheehan P ESnow E S 2010 Nano Lett. 10 3001
31Irmer SFrank TPutz SGmitra MKochan DFabian J 2015 Phys. Rev. B 91 115141
32Şahin HTopsakal MCiraci S 2011 Phys. Rev. B 83 115432
33Zhou JWang QSun QJena P 2010 Phys. Rev. B 81 085442
34Zhou JWu M MZhou XSun Q 2009 Appl. Phys. Lett. 95 103108
35Balog RJørgensen BNilsson LAndersen MRienks EBianchi MFanetti MLægsgaard EBaraldi ALizzit SSljivancanin ZBasenbacher FHammer BPedersen T GHofmann PHornekær L 2010 Nat. Mater. 9 315
36Zhou JWang QSun QChen X SKawazoe YJena P 2009 Nano Lett. 9 3867
37Liu ZSuenaga KHarris P J FIijima S 2009 Phys. Rev. Lett. 102 015501
38Borysiuk JSołtys JPiechota J 2011 J. Appl. Phys. 109 093523
39Rakhmanov A LRozhkov A VSboychakov A ONori F 2012 Phys. Rev. Lett. 109 206801
40Sboychakov A ORozhkov A VRakhmanov A LNori F 2013 Phys. Rev. B 88 045409
41de Andres P LRamírez RVergés J A 2008 Phys. Rev. B 77 045403
42de Andres P LGuinea FKatsnelson M I 2012 Phys. Rev. B 86 245409
43Segall M DLindan P J DProbert M JPickard C JHasnip P JClark S JPayne M C 2002 J. Phys.: Condens. Matter 14 2717
44Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
45Delley B 2010 J. Phys.: Condens. Matter 22 384208
46Heyd JScuseria G EErnzerhof M 2003 J. Chem. Phys. 118 8207
47Ming W MBlair SLiu F 2014 J. Phys.: Condens. Matter 26 505302
48Yang LDeslippe JPark C HCohen M LLouie S G 2009 Phys. Rev. Lett. 103 186802
49Yang L 2011 Nano Lett. 11 3844