Stimulated by the isolation of graphene from graphite, other two-dimensional (2D) layered materials with weak inter-layer van de Waals interaction (vdW), such as hexagonal boron nitride (h-BN) and phosphorene (P), were also isolated by liquid exfoliation routes^[1] and the mechanical exfoliation method.^[2,3] These 2D layered materials have attracted intensive research interest due to their fascinating electronic properties and extensive applications.^[4–9] Among them, h-BN is an insulator with a large band gap,^[10–12] which makes it difficult to tune the source–drain current using a gate voltage, therefore, h-BN has not yet been treated as a channel material in field-effect transistor (FET) fabrication. However, associated with its high purity, superior thermal and chemical stabilities, h-BN has emerged as a suitable dielectric to combine graphene or other graphene-like 2D crystal to create novel highly tailored heterostructures. For instance, Dean et al. reported that graphene devices on h-BN substrates have carrier mobilities and inhomogeneities that are almost an order of magnitude better than the devices on SiO₂.^[13] Theoretical studies have also shown the spontaneous opening and tuning of band structures of graphene on or between h-BN.^[14,15]

Recently, a new 2D material, phosphorene, a single layer of black phosphorus (BP) patterned into a hexagonal puckered lattice,^[16] has attracted considerable experimental and theoretical interest. Besides graphene, phosphorene is another stable elemental 2D monolayer which can be mechanically exfoliated experimentally.^[3] Phosphorene has a unique band structure, its highly anisotropic effective masses and electronic properties can be tuned by strain and electrical field, leading to a sequence of transitions among direct semiconductor, indirect semiconductor, semimetal, and metal.^[3,17–21] Moreover, this new layered material has a high charge-carrier mobility at room temperature^[2,3] and a band gap that changes considerably as a function of the number of layers, going from 0.31 eV for the bulk black phosphorus to around 1.51 eV for a monolayer.^[22]

Despite the promising physical properties explored in the phosphorene, it has been shown that the phosphorus suffers from oxidative degradation in the ambient conditions.^[23] Thus, how to protect the phosphorene from degradation is a central research topic. Currently, vertical heterostructures based on 2D van der Waals materials have been considered as a novel way to construct devices that integrate the properties of their isolated components^[24–27] with potential applications in optoelectronics^[28–31] and nanoelectronics.^[32,33] When two or more different 2D layered materials are assembled together, their properties may be preserved without any degradation. For example, a truly 2D nano-transistor has been constructed using heterostructures of graphene, h-BN, and MoS₂, where graphene acts as both source or drain and gate electrodes, h-BN as the high-k dielectric, and MoS₂ as the channel.^[34] Several phosphorene based heterostructures have also been reported with diverse applications in more flexible ways, such as phosphorene/graphene,^[27,35] phosphorene/MoS₂,^[32,36] and phosphorene/TiO2.^[37] Very recently, BP/BN field effect transistors have been synthesized.^[38] To the best of our knowledge, there is still a lack of systematic study of the effect of the BN monolayer capping on phosphorene.

In this paper, we choose the BN monolayer to protect phosphorene from degradation in the atmosphere and investigate the electronic properties of this hybrid nanocomposite. The results show that h-BN interacts weakly with the phosphorene via van der Waals interaction, both the properties of the phosphorene and BN are preserved in the nanocomposite. Moreover, interlayer interactions between the phosphorene and h-BN could induce tunable band gaps.

We perform first-principles study using state-of-the-art ab initio simulations, which are based on the density functional theory (DFT) as implemented in the VASP code.^[39,40] The spin unrestricted generalized gradient approximation of Perdew–Burk–Ernzerhof (PBE)^[41] and the projector augmented wave (PAW)^[42] are adopted to treat the ion–electron interactions. The plane-wave cutoff energy for the wave function is set to 500 eV. The van der Waals-corrected function, optB88-vdW,^[43,44] is used to account for the dispersion force between the atomic layers. OptB88-vdW has been demonstrated to reliably describe phosphorene systems^[22,36,45] and BN systems.^[46] The vacuum space in the z direction is about 15 Å to avoid the interaction between adjacent sheets due to the periodic image. During the geometric optimization, both lattice constants and atomic positions are relaxed until the residual forces on the atoms are smaller than 0.005 eV/Å and the total energy change is smaller than 1.0 × 10⁻⁵ eV. The GGA approach is well known to underestimate the band gap of semiconductors, the screened hybrid HSE06^[47] method is also used to give the accurate band structures. To assess the stability of the heterostrcture, we calculate the binding energy E_b per P atom as follows:

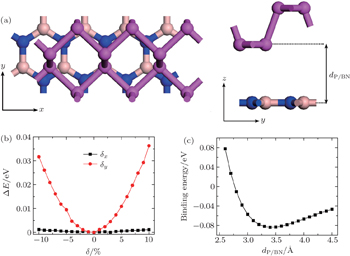
We construct a bilayer P/BN heterostructure by combining a 3 × 1 supercell of phosphorene with 12 P atoms and a 4 × 1 primitive orthorhombic cell of one BN layer with 8 B atoms and 8 N atoms. The optimized lattice constants of phosphorene are 3.30 Å and 4.62 Å along the x and y directions, respectively. For BN, the edge length of the basic hexagon is 2.51 Å. Since the electronic properties of phosphorene are sensitive to the strain,^[19] we keep the phosphorene lattice fixed, and stretch the BN system to compensate the lattice mismatch. The supercell of the heterojunction is chosen to be 9.72 Å and 4.54 Å along the x and y directions, respectively. The same strategy was used in the previous studies for hybrid layers.^[27] A lattice mismatch of around 3.3% compressive strain along the x direction and 4.4% tensile strain along the y direction occurs in BN, and no significant change is observed in its electronic structure. To obtain the equilibrium geometry, we optimize the composed structure using various starting positions of the phosphorene relative to the BN one. The stable configuration of P/BN stacked in the AB pattern is shown in Fig. 1(a). Starting from this configuration, we displace the phosphorene with respect to the BN layer by finite amounts δ_x (or δ_y) to further confirm the configuration. Figure 1(b) shows the evolution of the total energy difference (δE) as a function of δ.The energy change along the y direction is pronounced, and δE is almost independent of the relative position between the P and BN layers along the x direction. Moreover, since the binding energy difference for the displacements within 1% is quite small, it may be possible that the phosphorene is trapped in a position close to the lowest energy configuration during the growth process. For several displacements δ_x and δ_y, we calculate the corresponding electronic structure and compare with that at the equilibrium position (see Fig. 2). Negligible change is observed, therefore we focus on the most stable configuration in the following content.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Top and side views of P on top of BN. The dark-magenta, light-pink, and blue balls represent phosphorus, boron, and nitrogen atoms, respectively. (b) Evolution of the total energy as a function of the displacement δ of the phosphorene layer relative to BN, taking the origin at the lowest energy configuration. (c) Binding energy as a function of the distance dP/BN.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Band structures (upper panel) and atomic structures of P/BN (lower panel) for (a) equilibrium configuration; (b) δx = 0.5 Å; δy = 0.0 Å; (c) δx = −0.5 Å, δy = −0.5 Å; and (d) δx = 1.0 Å, δy = 0.0 Å. The red dashed lines are drawn as a guide with respect to the equilibrium configuration in panel (a).

The binding energy of the junction is calculated to be 84 meV with an equilibrium distance of 3.49 Å, as shown in Fig. 1(a). This value has the same order of magnitude as that in other van der Waals systems, such as bilayer graphene (50 meV), graphite (61 meV), and bulk hexagonal boron nitride (65 meV).^[46] The bond angle and bond length in the P/BN heterostructure system are almost the same as those observed in an isolated individual layer, which implies that no covalent bond forms in the junction and the weak vdW interaction is dominated in the heterostructure. In Fig. 3(a), we present the band structures of the P/BN junction, the pristine phosphorene, and the BN monolayer. The band gap of phosphorene is 1.59 eV and the BN monolayer has an indirect band gap of 5.69 eV with HSE06, which are in good agreement with the previous calculations.^[17,48] The weak interaction between phosphorene and BN solely results in a band gap decrease of 0.07 eV, the shapes of the valence band maximum (VBM) and the conduction band minimum (CBM) are almost the same as those of an isolated phosphorene layer. Therefore, the electrical transport behavior of the P/BN heterostructure will still be governed by the phosphorene. The projected density of states (PDOS) for the P/BN heterostructure are shown in Fig. 3(b). For the junction, the states around the Fermi level are contributed entirely by the 3p states of the P atoms, while the contributions of the B and N atoms are far from the Fermi level, outside the energy region [−1.0 eV, 4.7 eV]. As a result, we propose that the electronic properties of the phosphorene are preserved.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Band structures of P/BN (black), pristine phosphorene (red), and BN monolayer (blue). (b) Projected density of states of P/BN heterostructure.

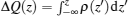
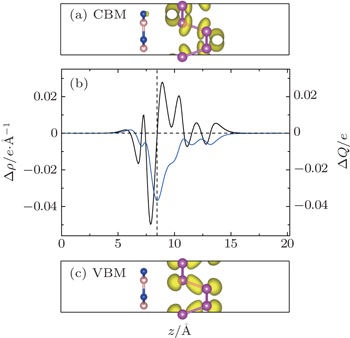
We then analyze the charge transfer in the junction. Figure 4 shows the planar-averaged differential charge density along the direction normal to the junction, and the decomposed charge densities of VBM and CBM both locating at the Γ point. It can be seen that the BN layer donates electrons to the phosphorene, indicating p-doping in the former and n-doping in the latter. The transferred charge is obtained by and the calculated value is 0.037e. From the charge density plots in Figs. 4(a) and 4(c), it is also clear that the charge of VBM and CBM mainly distributes at the more electronegative P atom, demonstrating that the electronic structure of the phosphorene is negligibly affected by the BN sheet, and the interaction between the phosphorene and BN is very weak.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Decomposed charge distributions of (a) CBM and (c) VBM in the yz plane for the P/BN heterostructure. The yellow represents the charge distributions of CBM and VBM with an isovalue of 0.01 e/Å3. (b) Planar-averaged differential charge density δρ(z) (black) and the amount of transferred charge δQ(z) (blue) in the hybrid P/BN nanocomposite at equilibrium distance in the z direction.

We reveal the tunable band gaps in P/BN by varying the interlayer distance, as plotted in Fig. 5(a). The band gap increases from 0.67 eV to 1.36 eV (GGA) as the interfacial distance decreases from 4.5 Å to 2.7 Å, which shows the tunability for application in nanoelectronics. Figure 5(b) presents the plane-averaged electrostatic potentials of the nanocomposite at different interfacial distances. As the interlayer distance decreases, the increased interaction between the BN and P layers enhances the charge transfer.^[49,50] While as the interfacial distance increases, the energy level of BN reduces slightly and the tunneling energy barrier at the P/BN interface for electrons will increase.^[51] The potential drop across the junction is about 3.86 V. Such a large potential difference means a strong electrostatic field across the interface, which may obviously impact the carrier dynamics and charge injection if the BN is served as the electrode.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) The band gap of the P/BN heterostructure as a function of the interfacial distance. The BN layer is fixed and only the phosphorene layer is moved away from the BN layer. The red dot represents the equilibrium position. (b) Plane-averaged electrostatic potentials of P/BN at different interfacial distances dP/BN (Å).

We have studied the structural and electronic properties of a hybrid P/BN nanocomposite using first-principles calculations. We show that the phosphorene interacts weakly with the BN sheet via weak vdW interaction which preserves their intrinsic electronic properties. Moreover, the variation of the interlayer distance could induce tunable band gaps in the hybrid P/BN nanocomposite. The redistribution of the electrostatic potential across the interface suggests that BN can serve as an active layer to tune the carrier dynamics of the phosphorene. With the excellent electronic properties superior to simplex BN and phosphorene monolayers, the 2D ultra-thin hybrid P/BN nanocomposite system is expected to possess great potential in new electronic devices.