Cite this Article
Ahmed Shabbir, Zafar Muhammad, Shakil M, Choudhary M A. Density functional theory study of structural, electronic, and thermal properties of Pt, Pd, Rh, Ir, Os and PtPd X (X = Ir, Os, and Rh) alloys. Chinese Physics B, 2016, 25(3): 036501  
Permissions
Density functional theory study of structural, electronic, and thermal properties of Pt, Pd, Rh, Ir, Os and PtPd X (X = Ir, Os, and Rh) alloys
Ahmed Shabbir1, †, , Zafar Muhammad1, Shakil M2, Choudhary M A1
Simulation Laboratory, Department of Physics, the Islamia University of Bahawalpur, Bahawalpur 63100, Pakistan
2Department of Physics, Hafiz Hayat Campus, University of Gujrat, Gujrat 50700, Pakistan

 

† Corresponding author. E-mail: shabir sehr@hotmail.com

Abstract
Abstract

The structural, electronic, mechanical, and thermal properties of Pt, Pd, Rh, Ir, Os metals and their alloys PtPdX (X = Ir, Os and Rh) are studied systematically using ab initio density functional theory. The groundstate properties such as lattice constant and bulk modulus are calculated to find the equilibrium atomic position for stable alloys. The electronic band structure and density of states are calculated to study the electronic behavior of metals on making their alloys. The electronic properties substantiate the metallic behavior for all studied materials. The firstprinciples density functional perturbation theory as implemented in quasi-harmonic approximation is used for the calculations of thermal properties. We have calculated the thermal properties such as the Debye temperature, vibrational energy, entropy and constant-volume specific heat. The calculated properties are compared with the previously reported experimental and theoretical data for metals and are found to be in good agreement. Calculated results for alloys could not be compared because there is no data available in the literature with such alloy composition.

PACS: 61.50.–f;71.15.Mb;71.20.Be
Keyword:electronic;structural and thermal properties;platinum group metals
1. Introduction

The platinum group metals (PGMs) are promising materials for numerous technological applications. The four PGMs Pt, Pd, Ir, and Rh have face-centered cubic (fcc) and other two OS and Ru has hexagonal close-packed (hcp) structure. PGMs are considered as primary ingredients in the automotive, chemical, and petroleum industries. Their thermal stability at high temperatures and the highest shear modulus at room temperature make them superior materials.[1–3] They have been investigated for carbon material protective coatings,[4] heavy-metal-ion sensors,[5] and Re-rocket thrust[6] applications. They are also broadly used in organic chemistry for hydrogenation, hydro-formylation, hydro-boration, hydro-silylation, cyclo-additions,[7,8] and oxidation reactions for the catalytic converters in automobiles. Their incredible catalysis activity increases research interests in these rare elements,[9] but odd with their higher cost. The importance and higher cost of PGMs motivate the researchers for the development of alloys to reduce the material cost and changing in properties to the requirement. The transition metals and their inter-metallic alloys are promising structural materials because of their high melting points, high strength, and good oxidation resistances.[10] During the recent years, the inter-metallic alloys of these PGMs have attracted considerable experimental and theoretical interests of many researchers.[11] Many of the possible alloy compositions have not yet been studied and there are still sizable gaps in the knowledge of the basic properties, especially thermal properties of PGMs and their alloys. There is a considerable difficulty in calculating thermodynamic properties experimentally because they often require high temperatures or pressures and very long equilibration processes.

Ab initio technique based on density-functional theory (DFT)[12–14] has been used to calculate the properties of materials at zero temperature in the last few decades. However, the first-principles approaches in the study of thermal properties are still challenging for researchers. A simplified approach for thermal properties calculation is Debye–Gruneisen theory[15] that maybe used properties calculations[16,17] as well as for compounds.[18] The Car–Parrinello first-principles molecular dynamics simulations method is being used for more accurate thermodynamic properties calculations.[19] However, this simulation method can be a heavy computational task and results may not be realistic enough. Now it is possible to calculate vibrational frequencies at every point of the Brillouin zone with the achievements of density-functional perturbation theory (DFPT).[20,21] This method also has reduced computational time for thermal properties and many applications have been made within DFPT.[22] In this approximation, an harmonic effect is included through the explicit volume dependence of the vibrational frequency. Several thermal expansion calculations for cubic metals based on DFPT have been carried out[23–26] and they give good results about isotropic thermal expansion and related thermal properties. In this paper we apply quasi harmonic approximation with DFPT to the study of the thermal properties of platinum group metals and their alloys. A relatively dense mesh of k points is needed to achieve convergence of phonon frequencies for both metals because of complexities of the Fermi surface.[27]

2. Computational method

The first-principles investigation was performed using a pseudo-potential plane wave (PP-PW) method as implemented in QUANTUMES ESPRESSO.[28] We have used super cell with 2 × 2 × 2 dimension to study PGMs and their alloys. Super cell with Pt0.25Pd0.25X0.50 concentration was used for PtPdX (X = Ir, Os and Rh) alloys. Vanderbilt ultra-soft pseudo-potential parameterized by Perdew and Zunger[29,30] was used for calculations. We used ultra soft Vanderbilt formalism with local density approximation (LDA)[31] for the exchange correlation energy of the electrons. The special k-points mesh was integrated to sampled Brillouin zone using the Monkhorst–Pack method.[32] A special k-points mesh of 14 × 14 ×14 was used to produce irreducible Brillouin zone. The pseudo-wave functions were expanded in a plane wave basis set using cut-off energy of 30 Ryd for all concentrations. The chosen cut-off energy and k-point mesh ensure convergence with an accuracy of 10−6 Ryd. DFPT and quasi-harmonic approximation (QHA) code developed by Baroni et al.[28] was used to investigate phonon density of states and thermal properties from optimized structure. The dynamical matrices at arbitrary wave vectors were obtained using Fourier transformation based interpolations for thermal properties calculations. A 10 × 10 × 10 q point mesh was implemented to obtain force constants dynamical matrices in the irreducible Brillouin zone at Γ point. The linear response approach method was used to obtain phonon density of states curves within the frame-work of DFPT[28] as implemented in quantum ESPRESSO.

The parameters such as cell dimension, energy cut-offs, and the k-points used in the study were obtained from their respective convergence tests. These convergence parameters provide a fast way toward the optimized structure.

3. Results and discussion
3.1. Structural properties

We have calculated the ground state properties of Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os, and Rh) to find out the crystal structure. Total energy per unit cell was computed at various lattice parameters to find the equilibrium lattice constant. The total energy minimization method was used to obtain equilibrium lattice constant. For this purpose, Murnaghan’s equation of state was used to evaluate the optimized lattice constants and bulk modulii.[33] The structural parameters, i.e. lattice constants and bulk modulus, were calculated for pure Pt, Pd, Rh, Ir, Os, and their alloys, and are reported in Table 1 along with experimental and other theoretical results. The optimized lattice curves for Pt, Pd, Rh, Ir, Os are shown in Fig. 1 and for their alloys PtPdX (X = Ir, Os, and Rh) are presented in Fig. 2.

Table 1.

Comparison of calculated lattice parameters and bulk modulus of Pt, Pd, Rh, Ir, Os, and their alloys PtPdX (X = Ir, Os, and Rh) with experimental and other theoretical results.

.
Fig. 1. Structural optimization plots for pure metals: (a) Pt, (b) Pd, (c) Ir, (d) Rh, and (e) for Os.
Fig. 2. Structural optimization plots of (a) Pt0.50Pd0.50, (b) Pt0.25Pd0.25Ir0.50, (c) Pt0.25Pd0.25Rh0.50, and (d) Pt0.25Pd0.25Os0.50 alloys.
3.2. Electronic properties

The electronic properties provide information about the material’s electronic configuration, particularly the existence of prohibited regions of energy and the magnitude in their electronic excitation spectral. Hence, the band structures for Pt, Pd, Rh, Ir, Os, and their alloys PtPdX (X = Ir, Os, and Rh) along various high-symmetry directions were calculated at equilibrium lattice constants. The electronic band structures for pure metals (Pt, Pd, Rh, Ir, Os) are shown in Figs. 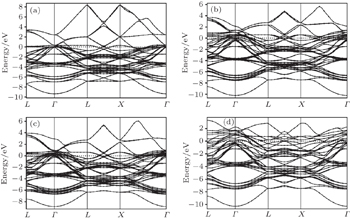3(a)–3(e) and for their alloys PtPdX (X = Ir, Os, and Rh) are shown in Figs. 4(a)–4(d). The Fermi energy level for electronic band structure was set to be at 0 eV. It can be seen from Figs. 3 and 4 that electronic bands for all metals and their alloys overlap at the Fermi level. The conductivity in Pt, Pd, and Rh metals is dominated by overlapping s and d bands. In Ir and Os, the hybridization is between s, p, and d bands. Their alloys PtPdX (X = Ir, Os and Rh) show metallic nature due to broad d bands of metals which contribute in these alloys.

Fig. 3. Calculated band structures for pure metals: (a) Pt, (b) Pd, (c) Ir, (d) Rh, and (e) Os.
Fig. 4. Calculated band structures for (a) Pt0.50Pd0.50, (b) Pt0.25Pd0.25Ir0.50, (c) Pt0.25Pd0.25Rh0.50, and (d) Pt0.25Pd0.25Os0.50 alloys.

The main hybridization was remained between d bands of metals to form their alloys. It was observed from the analysis of band structure of all given metals and their alloys that they all have similar behavior. However, it is also observed that they mainly differ from each other by the energy level relative to the Fermi level. The calculated electronic band structure is in good agreement with previous results for pure metals, i.e. Ir, Rh, Pt, Pd, and Os.[52–56] Calculations of their studied alloys may be reported for the first time. Therefore, there is no previous data available for the comparison to these alloys.

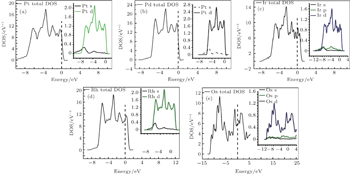
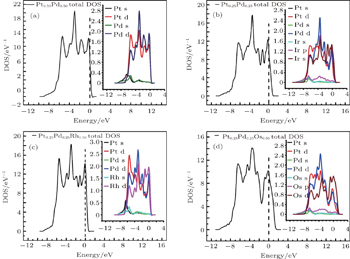
Many physical properties can be studied with the help of density of states (DOS). Specially, it plays a significant role to study the electronic properties of materials and is more important to explore the electronic band structure. From Figs. 5(a), 5(b), and 5(d), it can be observed that the lowest lying bands for Pt, Pd, and Rh metals are due to s states. On the other hand, the higher energy states are mainly due to d states and the conductivity seems to be dominated by s–d hybridization states. Furthermore, it can also be seen from Figs. 5(c) and 5(e) that, for Ir and Os the lowest lying bands are due to s and p states and the higher energy states due to d states as well as the conductivity considered to be dominated by s, p, and d hybridization states.

Fig. 5. DOS calculated for pure metals: (a) Pt, (b) Pd, (c) Ir, (d) Rh, and (e) Os.

In Fig. 6(a), with Pt0.50Pd0.50 concentration, the lowest part of valance band was found to be generally contributed by s state of both metals, but the higher energy level was dominated by broad contribution of d states of these metals. In the case of Pt0.25Pd0.25Ir0.50 alloy, from Fig. 6(b), the bottom state of the valence band was dominated with s and p states of Ir and s state of Pt and Pd. The upper valance band region was dominated with d states of Ir, Pt, and Pd with some contribution of other lower energy states. In Fig. 6(c) with PtPdOs, the lowest part of valance band was contributed by s and p states of Os and s state of Pt and Pd state, but the higher energy level was dominated by broad contribution of d states of these metals with little part of other states. In Fig. 6(d) for PtPdRh, s states of Pt, Pd, and Rh for the said alloy dominated the bottom of the valence band, but their higher energy levels are dominated by broad contribution of d states of these metals with little part of other states.

In pure metals, i.e., Pt, Pd, and Rh, the conductivity was mostly dominated by s and d hybridization. However, for Ir and Os, hybridization was due to s, p, and d states. The DOS is compared with the results available in literature for Ir, Rh, Pt, Pd, and Os metals.[57–61]

When these metals were mixed to make alloys, the strong hybridization between the d states with small contribution of s states dominated the conductivity. The calculated DOS for various metals and their alloys showed that Rh has high DOS energy at Fermi level among the studied systems. Therefore, it is affirmed that the Rh metal has good conductivity due to its high DOS at Fermi level and its concentration in alloy PtPdRh increases the electronic conductivity.

Fig. 6. DOS calculated for (a) Pt0.50Pd0.50, (b) Pt0.25Pd0.25Ir0.50, (c) Pt0.25Pd0.25Rh0.50, and (d) Pt0.25Pd0.25Os0.50 alloys.
3.3. Thermal properties

Materials’ thermal properties have interesting characteristics below the melting temperature. The knowledge of materials’ thermal properties is very important for developments and manufacturing electronic devices.[62,63] Phonon DOS and quasiharmonic approximation were used to obtain thermal properties. Debye temperature, Helmholtz free energy ΔF, internal energy ΔE, entropy S, and constant-volume specific heat Cv at zero pressure are calculated using the following relations:[64]

where kβ is the Boltzmann constant, n is the number of atoms per unit cell, N is the number of unit cells, ωmax is the largest phonon frequency, ω is the phonon frequency, and g(ω) is the normalized DOS with .

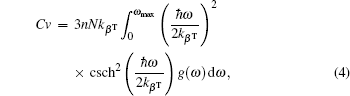
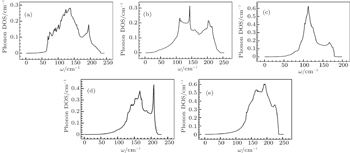
Phonon DOS has strong impact on thermodynamic properties and electron excitation can be investigated with the help of phonon DOS.[65] We have studied total and partial phonon density of states of metals Pt, Pd, Rh, Ir, Os, and their alloys.

Figures 7 and 8 depict phonon density of states for metals Pt, Pd, Rh, Ir, Os, and their alloys PtPdX (X = Ir, Os, Rh). From Figs. 7(a)–7(e), it was analyzed that Pt, Pd, Rh, Ir, and Os have most prominent phonon DOS at frequencies 123, 143, 155, 112, and 193 cm−1. In Fig. 8(a), phonon DOS was due to movement of Pt and Pd at lower frequencies (50–110 cm−1). However, at higher frequencies (140–215 cm−1) phonon DOS was contributed by Pd. Two higher peaks in phonon DOS occur for PtPdIr, PtPdRh, and PtPdOs alloys as shown in Figs. 8(b)–8(d). First phonon DOS peak is dominated by Ir, Rh, Os, and second was due to Pd atoms in alloys PtPdIr, PtPdRh, and PtPdOs. Phonon DOS for Rh was observed large among the studied metals and their alloys for higher frequencies. Phonon density of states is in comparable with other calculation.[66]

Fig. 7. Phonon DOS for pure metals: (a) Pt, (b) Pd, (c) Ir, (d) Rh, and (e) Os.
Fig. 8. Phonon DOS for (a) Pt0.50Pd0.50, (b) Pt0.25Pd0.25Ir0.50, (c) Pt0.25Pd0.25Rh0.50, and (d) Pt0.25Pd0.25Os0.50 alloys.

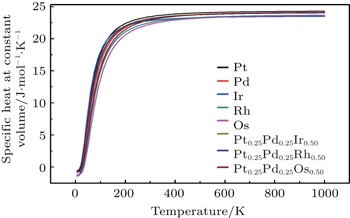
To investigate the more thermal properties, we have calculated the thermal properties such as Debye temperatures, vibration energy, entropy and constant-volume specific heat and are plotted in Figs. 9–12. Debye temperature determines the thermal characteristics of materials and it is closely related to many physical properties such as specific heat, vibration energy, entropy, thermal conductivity, and melting temperature.[67] It was perceived from the analysis of Debye temperature of metals and their alloys that Rh has large value. Therefore, it is considered that, Rh requires more energy to activate all the phonon modes in crystal due to its high Debye temperature at 300 k. Entropy and constant-volume specific heat were found to be increased with temperature and these properties describe materials interesting characteristics. Different materials have different specific heat capacity because molecules vibrate back and forth differently due to strong or weak bounded atoms. It was observed that platinum has high entropy and specific heat capacity at constant volume among the studied materials. Therefore, platinum possesses many attractive properties that suggest its great potential in a wide variety of applications.[68–73] It has also been observed that vibrational energy decreases with temperature.

Our calculated results for thermal properties for pure metals, i.e., Ir, Rh, Pt, Pd, and Os, are in good agreement with the previous findings.[74–78] There were no experimental or theoretical results available in the literature for their alloys. Therefore, the results reported in this work will be predictive for future.

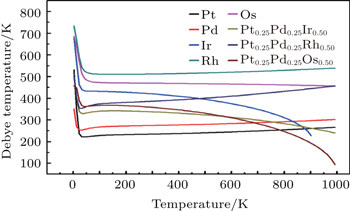Fig. 9. Debye temperature variation with temperature for Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os and Rh) alloys.
Fig. 10. Vibration energy variation with temperature for Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os, and Rh) alloys.
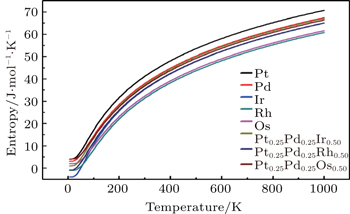Fig. 11. Entropy variation with temperature for Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os, and Rh) alloys.
Fig. 12. Specific-heat at constant volume variation with temperature for Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os, and Rh) alloys.
4. Conclusions

We employed the first-principles plane wave pseudo-potential DFT method to analyze the structural, electronic, mechanical, and thermal properties of the Pt, Pd, Rh, Ir, Os, and PtPdX (X = Ir, Os, and Rh) alloys. A super cell with 2 × 2 × 2 dimension was used for all calculations. A super cell with Pt0.25Pd0.25X0.50 concentration was used for PtPdX (X = Ir, Os, and Rh) alloys. The following conclusions are drawn.

Reference
1Savitskii E M1989Handbook of Precious Metals New YorkHemisphere Publishing Corporation
2Cawkwell M JNguyen-Manh DWoodward CPettifor D GVitek V2005Science 309
3Stevanovic VSljivancanin ZBalderesch A2007Phys. Rev. Lett.99165501
4Mumataz KEchigoya JHirai TShindo Y1993Mater. Sci. Eng. A167187
5Kovacs G T AStorment C WKounaves S P1995Sens. Actuators B2341
6Hamilton J CYang N Y CClift W MBoehme D RMcCarty K FFranklin J E1992Metall. Trans. A23851
7Evans P A 2005 Applied Organometallic Chemistry 19 11
8Lippard S J1981Progress in Inorganic ChemistryNJ, USAJohn Wiley & Sons
9Yuan YYan NDyson P J2012ACS Catalysis21057
10Colinet CPasturel A 2001 Phys. Rev. B 64 205102
11lebacq OPasturel AManh D NFinel ACaudron R1998J. Alloy. Compd.26431
12Hohenberg PKohn W 1964 Phys. Rev. B 136 864
13Kohn WSham L J 1965 Phys. Rev. A 140 1133
14Jones R OGunnarsson O 1989 Rev. Mod. Phys. 61 689
15Moruzzi V LJanak J FSchwarz 1988 Phys. Rev. B 37 790
16Jin H MWu P 2002 J. Alloy. Compd. 343 71
17Lu X GSelleby MSundman B 2005 Acta Mater. 53 2259
18Mayer BAntona HBotta E 2003 Intermetallics 11 23
19Car RParrinello M 1985 Phys. Rev. Lett. 55 2471
20Baroni SGiannozzi PTesta A 1987 Phys. Rev. Lett. 58 1861
21Giannozzi Pde Gironcoli SPavone PBaroni S 1991 Phys. Rev. B 43 7231
22Baroni Sde Gironcoli SCorso A DGiannozzi P 2001 Rev. Mod. Phys. 73 515
23Narasimhan Sde Gironcoli S2002Phys. Rev. B65064302
24Quong A ALiu A Y 1997 Phys. Rev. B 56 7767
25Xie Jde Gironcoli SBaroni SScheffler M 1999 Phys. Rev. B 59 965
26Debernardi AAlouani MDreysse H 2001 Phys. Rev. B 63 064305
27Heid RPintschovius LReichardt WBohnen K P 2000 Phys. Rev. B 61 12059
28Baroni SDal Corso AGironcoli SGiannozzi P2001Rev. Mod. Phys.73515
29Ceperley D MAlder B J1980Phys. Rev. Lett.45567
30Perdew J PZunger A1981Phys. Rev. B235048
31Vanderbilt D 1985 Phys. Rev. B 32 8412
32Monkhorst H JPack J D 1976 Phys. Rev. B 13 5188
33Murnaghan F D1944National Academy of Sciences of the United States of America30244
34Villars Pet al.1991Handbook of Crystallographic Data for Intermetallic Phases2nd edn. (ASM International)
35Rao C NRao K K1964Can. J. Phys.421336
36Haas PTran FBlaha F P 2009 Phys. Rev. B 79 085104
37Nygren L ALeisure R G1988Phys. Rev. B376482
38Schwarz R BBach H THarms UTuggle D2005Acta Meter.53569
39Bercegeay CBernard S 2005 Phys. Rev. B 72 214101
40Ono SJohn P 2011 J. Phys. Chem. Solid. 72 169
41Karbasi ASaxena S KHrubiak R 2011 Computer Coupling of Phase Diagrams and Thermo Chemistry 35 72
42Mehl M JPapaconstantopoulos D A1996Phys. Rev. B544519
43Gong H R2008Scripta Mater.591197
44Singh H P1998Acta Cryst. A24469
45Gomez JDing YKoitz RAri P SeitsonenIann M2013Theoretical Chemistry Accounts1321350
46Simmons GWang H1971A Handbook of Single Crystal Elastic Constants and Calculated Aggregate Properties2nd edn.CambridgeMIT Press
47Walker EAshkenazi JDacorogna M 1981 Phys. Rev. B 24 2254
48Manish KNiranjan 2012Intermetallics26150
49Hanan SBothina H2008J Phys. Chem. Solid692457
50Cynn HKlepeis J EYoo C SYoung D A 2002 Phys. Rev. Lett. 88 135701
51Liu KHe D WZhou X LChen H H 2011 Physica B 406 3065
52Ahuja B LSharma VRathor AJani A RSharma B K2007Nuclear Instruments and Methods in Physics Research B262391
53Noffke JFritsche L1982J. Phys. F12921
54Herrera-Suarez H JRubio-Ponce AOlguimathn D2012Rev. Mex. Fis.5846
55Mueller F MFreemant A JDimmock J OFurdyna A M1970Phys. Rev. B1
56Jepsen OKrogh Andersen OMackentosh A R1970Phys. Rev. B123084
57Bannikov V VShein I RIvanovskii A L2009Solid State Commun.1491807
58Sudhapriyanga GAsvinimeenaatcia A TRajeswarapalanichamy RIyakutti K2014Acta Phys. Polonica A12529
59Gianluca SAngelo VMarcella I 2008 J. Chem. Phys. 129 234703
60Bose S KKudrnovsky JMazin I IAndersen O K1990Phys. Rev. B4112
61Nemoshkalenko V VAntonov V NKirillova M MKrasovskii A ENomerovannaya L V1986Sov. Phys. JETP63115
62Newnham Robert E2005Properties of MaterialsNew YorkOxford
63Mattesini MMagnuson MTasnádi FHöglund CAbrikosov Igor AHultman L2009Phys. Rev. B79125122
64Maradudin A Aet al.1971Solid State Physics2nd edn.New YorkAcademic
65Liang C PGong H R2013Intermetallics3210.1016/j.intermet.2013.04.017
66Baria J KJani A R 2003 Physica B 328 317
67Boucetta SZegrar F2013J. Magn. Alloy.1128
68Chen S TTang W YKuo Y FChen S YTsau C HShun T TYeh J W2010Mater. Sci. Eng. A5275818
69Chuang M HTsai M HWang W RLin S JYeh J W2011Acta Mater.596308
70Hemphill M AYuan TWang G YYeh J WTsai C WChuang ALiaw P K2012Acta Mater.605723
71Hsu C YJuan C CWang W RSheu T SYeh J WChen S K2011Mater. Sci. Eng. A5283581
72Tsai M HWang C WTsai C WShen W JYeh J WGan J YWu W W2011J. Electrochem. Soc.158
73Chou Y LWang Y CYeh J WShih H C2010Corros. Sci.523481
74Gray D E1972American Institute of Physics Handbook3rd edn.New YorkMcGraw Hill
75Konti AVarshni Y P1969J. Phys.472021
76Nie Y ZXie Y QPeng H JLi X B 2007 Physica B 395 121
77Qiuping BianBose S KShukla R C 2008 J. Phys. Chem. Solid. 69 168
78Liu KHe D WZhou X LChen H H 2011 Physica B 406 3065