Cite this Article
Zhang Jin-Ping, Zhang Yang-Yang, Wang Er-Ping, Tang Cui-Ming, Cheng Xin-Lu, Zhang Qiu-Hui. Size effect in the melting and freezing behaviors of Al/Ti core-shell nanoparticles using molecular dynamics simulations. Chinese Physics B, 2016, 25(3): 036102  
Permissions
Size effect in the melting and freezing behaviors of Al/Ti core-shell nanoparticles using molecular dynamics simulations
Zhang Jin-Ping1, †, , Zhang Yang-Yang1, Wang Er-Ping1, Tang Cui-Ming2, Cheng Xin-Lu2, Zhang Qiu-Hui3
College of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450006, China
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Department of Electrical Information Engineering, Henan Institute of Engineering, Zhengzhou 451191, China

 

† Corresponding author. E-mail: jinping213@163.com

Project supported by the National Natural Science Foundation of China (Grant No. 21401064), the Science & Technology Development Program of Henan Province, China (Grant No. 142300410282), and the Program of Henan Educational Committee, China (Grant No. 13B140986).

Abstract
Abstract

The thermal stability of Ti@Al core/shell nanoparticles with different sizes and components during continuous heating and cooling processes is examined by a molecular dynamics simulation with embedded atom method. The thermodynamic properties and structure evolution during continuous heating and cooling processes are investigated through the characterization of the potential energy, specific heat distribution, and radial distribution function (RDF). Our study shows that, for fixed Ti core size, the melting temperature decreases with Al shell thickness, while the crystallizing temperature and glass formation temperature increase with Al shell thickness. Diverse melting mechanisms have been discovered for different Ti core sized with fixed Al shell thickness nanoparticles. The melting temperature increases with the Ti core radius. The trend agrees well with the theoretical phase diagram of bimetallic nanoparticles. In addition, the glass phase formation of Al–Ti nanoparticles for the fast cooling rate of 12 K/ps, and the crystal phase formation for the low cooling rate of 0.15 K/ps. The icosahedron structure is formed in the frozen 4366 Al–Ti atoms for the low cooling rate.

PACS: 61.46.Df;52.65.Yy;65.80.–g;
Keyword:molecular dynamics;melting;radial distribution function;structure evolution;
1. Introduction

The titaninum–aluminide intermetallic compounds have high melting points, high mechanical strength, oxidation resistance, and low density.[1,2] Therefore, these materials have received intensive interest recently in the automotive, aerospace, and power generation industries. A number of experimental[3–13] and theoretical[14–20] studies on Al–Ti systems have been carried out over the past several years. Most of the work is devoted to synthesis,[3–7] microstructure,[8–12] mechanical properties,[9–11] thermophysical properties,[13] etc. Up to now, increasing amount of interest has been paid to the nanostructured TiAl alloys because it can significantly improve the ductility and toughness.[21–23] The thermal and mechanical properties of nanoparticles (NPs) can display some unique behavior associated with the size-dependent properties, such as melting point depression and other low-dimension effects. Theoretically, these studies[14–20] have focused mainly on the rapid solidification,[14,15] synthesis,[16] effect of impurity,[17,18] and alloying reaction.[19,20] However, the understanding of the melting process of nanoparticles has not been addressed satisfactorily because thorough theoretical study on the melting behavior of the Ti core-Al shell at the atomistic level has rarely been reported.

Understanding the thermal stability of bimetallic nanoparticles is particularly important in view of their application. However, experimental investigations of melting are difficult, due to the constraints in conducting accurate experiments at nanoscale. Therefore, molecular dynamics (MD) simulation plays an essential role to study the melting and solidification behaviors. Most investigations have been used successfully in predicting the melting temperature and other properties of bimetallic NPs.[24–28] In our previous works,[29] the heating, cooling, and reactive behavior of core-shell structured Cu–Al NPs was investigated using molecular dynamics simulation. However, there is only one group[19,20] that studied the heating, cooling, and alloying reaction of the Ti-coated Al NPs. Little attention has been paid to the particle size and composition effect in the melting and freezing behaviors of Al–Ti NPs, which is very significant for producing various physical and chemical properties of bimetallic nanoparticles.

Obviously, thermodynamic properties are very important in research and applications, such as melting of the core shell NPs. In this study, we focus on the thermal stability of Al–Ti core-shell NPs with different sizes during continuous heating and cooling processes. Using embedded atom method (EAM), we perform MD simulations on bimetallic Al–Ti NPs with five different sizes, including fixed Ti core radius (Rc = 2 nm), different Al shell thickness (0.3, 0.5, and 0.7 nm), and fixed Al shell thickness (δs = 0.5 nm), different Ti core radius (3 and 4 nm). In all cases, the thermodynamic properties and structure evolution during continuous heating and under different solidification rates will be investigated through the characterization of the total potential energy distribution and radial distribution function (RDF), and some unique behaviors will be revealed.

2. Simulation model and method

Ti-core/Al-shell (denoted as Ti@Al) NPs are constructed from an fcc core of Al and an hcp shell of Ti (α-Ti). The bulk lattice constant of Al is aAl = 4.05 Å, while the bulk lattice constants of Ti are aTi = 2.95 Å and cTi = 4.68 Å. In order to trace the influence of the core/shell ratio, we have constructed Ti@Al NPs with a fixed core radius and different shell thicknesses, as well as a fixed shell thickness and different core radii for comparison in this study. For the fixed Ti core radii (Rc = 2 nm, contains 1904 Ti atoms), the thicknesses of Al shell can take values of 0.7, 0.5, or 0.3 nm (3662, 2462, or 1280 Al atoms, denoted as NP1, NP2, or NP3, respectively). Similarly, for the fixed Al shell thickness (δs = 0.5 nm, contain 4710 and 7866 Al atoms, respectively), the radius of Ti core is measured to be 3 and 4 nm (6493 and 15176 Ti atoms, denoted as NP4 and NP5, respectively). Ti@Al NPs is separated by a gap of 3.0 Å between the core and shell atoms, as illustrated schematically in Fig. 1. The total diameter for NP1, NP2, NP3, NP4, and NP5 of Ti@Al NPs are 6.0, 5.6, 5.2, 7.6, and 9.6 nm, corresponding to 5566, 4366, 3184, 11203, and 23042 atoms, respectively. The Ti/Al ratio increases from NP1 to NP5.

Fig. 1. (a) Schematic illustration and (b) atomic arrangement of Ti@Al nanoparticles. Grey: Ti atom; dark grey: Al atom. Note that R, Rc, and δs denote the particle radius, core radius, and shell thickness, respectively.

All molecular dynamics (MD) simulations are carried out with the LAMMPS software package.[30] The interatomic interactions are described by an embedded atom method (EAM) potential developed by Zope and Mishin.[31] The EAM potential is constructed by fitting to a large experimental database as well as ab initio data. This potential has been successfully used in previous investigations of fcc random alloys and NPs, demonstrating an accurate description of elastic properties and alloying reaction.[19,32] Therefore, the present EAM potential for investigating the Ti–Al system is reliable and accurate. An energy minimization process is performed for all the NPs before the MD simulation started. The time step in all calculations is 1.0 fs, which leads to quite stable dynamics trajectories for the system. Non-periodic boundary conditions are used to ensure the simulation of isolated NPs during the simulation process. All the MD simulations are carried out in the canonical ensemble (NVT) with the application of the Nosé–Hoover thermostat. For the heating simulation, each nanoparticle is first relaxed for 100 ps at 300 K. Then a constant rate of heating (0.6 K/ps) is employed in the heating simulation; i.e., NP1, NP2, and NP3 are heated gradually for 2×106 time steps, which is equivalent to 2000 ps, with the temperature rising from 300 K to 1500 K, while NP4 and NP5 are heated stepwise from 300 K to 2100 K with a time step of 3000 ps. For the solidification simulation, an additional relaxation time of 100 ps at 1500 K is conducted before implementing the cooling process. Three quenching rates for solidification are simulated: 12 K/ps, 6 K/ps, and 0.15 K/ps, corresponding to runtimes of 1.0 × 105, 2.0 × 105, and 8.0 × 106 fs.

3. Results and discussion
3.1. Heating simulation

The thermodynamics properties, the characteristics, and the progress of the Ti@Al NPs melting during the heating process can be obtained from data records by MD simulations. Generally, the transition temperature from the solid to liquid phase is usually identified by investigating the variation in the thermodynamic properties such as potential energy and specific heat. Note that the specific heat can be induced as a function of temperature according to the following equation:[33]

where U is the potential energy and Rgc = 8.314 J/(mol·K).

For a constant heating rate of 0.6 K/ps, the temperature dependence of potential energies and specific heat for five Ti@Al NPs is shown in Fig. 2. It can be seen that, the total potential energy decreases with Ti content. This is mainly caused by the lower potential energy of Ti with respect to Al. We also find that, the potential energy for every NP has a linear increase followed by an abrupt jump, occurring due to the release of latent heat of melting. These can be seen clearly in all cases of pure and bimetallic nanoparticles of different composition.[25–28] Hence, the solid–liquid phase transition can be easily revealed by the abrupt change of the potential energy and the sharp peak of the specific heat. The melting point Tm is usually defined as the temperature at which an abrupt jump in potential energy takes place or the temperature at which the specific heat reaches its maximum. The melting temperatures of the five Ti@Al NPs, deduced from the caloric curves, are shown in Table 1. From Fig. 2 and Table 1, it can be seen that for fixed Ti core size, the melting temperature decreases with Al shell thickness. The calculated results can be attributed to the fact that elementary Al possesses an extremely lower melting point than Ti. Therefore, the thinner the Al shell is, the higher composition of Ti, resulting in a higher melting temperature. For different Ti core sized with fixed Al shell thickness, the melting temperature increases with Ti core size. This result demonstrates that for five Ti@Al NPs, Tm gradually increases with Ti composition from NP1 to NP5.

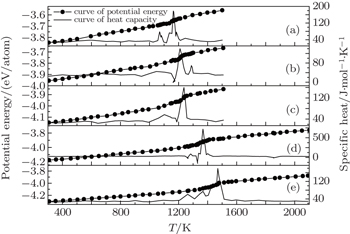Fig. 2. Temperature-dependent potential energies and specific heat for five different NPs during the heating process. (a) NP1; (b) NP2; (c) NP3; (d) NP4; (e) NP5.
Table 1.

Melting temperature Tm for different NPs.

.

In order to visualize the melting process and to shed light on the melting mechanism, we have investigated atomistic structural evolution of the Ti@Al NPs during the heating process. As a representative, NP2 has been used to exhibit the thermal evolution of core/shell NPs under the continuous heating process. Figure 3 shows the snapshots during continuous heating. Figure 3 displays the two-dimensional cross-sectional view cut through the center of mass. Since the volume of the whole system is constant, these snap shots are taken as radial representations of the whole system. At the lower temperatures, e.g., T = 0 K and 350 K, the Ti@Al NP can retain its initial clear-cut fcc arrangement, which is clearly seen in Fig. 3. When increasing the temperature to 700 K, several surface atoms left their edge location as seen in the snapshots, indicating the premelting occurs on the surface of Al shell firstly. At 1050 K, the position of Al atoms becomes disorderly, but most of the Ti atoms in the core stably preserve the order lattice, indicating the melting of the Al shell. It is concluded that the premelting process of Ti@Al NPs starts from the edge, and then extends to the whole Al surface. At this time, the bimetallic NP can be regarded as a liquid-like Al encapsulated solid Ti particle. This morphology is chemically interesting because the liquid metal atoms on the surface of solid particles may facilitate the dissolution of adsorbates due to their enhanced mobility, enabling the occurrence of different chemical processes.[34] Further elevated temperature could make the melting spread into inner Ti core. At higher temperatures, T = 1250 K, above the melting temperatures, the initial crystalline structure has been completely lost. The global melting is obvious in the snapshots of the NP2 in Fig. 3. The temperature distinctly exceeds the melting points of Al NPs but lower than Tm that of corresponding size pure Ti NPs, meaning that the core/shell structure can be significantly elevated melting temperature of Al shell and reduced melting point of Ti core. We also find that a two-way diffusion is clearly visible, i.e., the Ti core atoms diffusing outward and the shell Al atoms diffusing inward. With the temperature increased to 1500 K, Ti atoms have rapidly diffused into the Al shell due to their enhanced mobility after melting, resulting in the disappearance of core-shell interfacial structure, a well mixed liquid Ti@Al functional droplet forms. The aforementioned results show that the melting of Ti@Al NPs has experienced from surface into interior, exhibiting a distinct two-stage process.

Fig. 3. Snapshots of the evolution of NP2 during a heating process (Al atoms are colored in dark grey, while Ti atoms are in grey).

Radial distribution function (RDF) is of importance to the analysis of particle structures and properties. RDF gives the local atomic arrangement and is a tool to distinguish between solids and liquids. The heights of the RDF peaks manifest the local order of structure. While crystalline solids are characterized by a repeating sequence of sharp peaks separated by distances between neighbors, RDF for liquids has few peaks at short distances and no long range order. Here, we use RDF to support above conclusion that the shells melt first and then the cores for core/shell Ti@Al NPs. We calculate the RDF of the core and the shell for Ti@Al core/shell NP2 of 4366 atoms, the results shown in Fig. 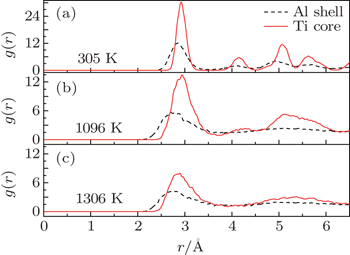4. From the curve, the sharp characteristic peaks can be seen clearly, which shows that the core and the shell keep the FCC structure at 300 K. At 1096 K, the number of the peaks of the core reduced, at the same time, the value of the peaks also drop, indicating that its long-range order become weak, but the FCC structure still remains. To the shell, the first peak of the curve becomes lower and wider, but the other peaks almost disappear totally, these illustrate that the shell loses its long-range order and become liquid. As the temperature rises to 1306 K, to the core and the shell, the value of the first peak is lower than 1096 K, and other peaks disappear, which means that Ti@Al NPs all melt.

Fig. 4. RDF of core and shell for Ti@Al core/shell NPs of 4366 atoms (NP2) at 305, 1096, and 1306 K.

Single-particle MD simulations are also conducted on pure Ti NPs to establish a comparative basis for the heating study of the five different NPs. The melting temperature for three different-sized pure Ti NPs is also listed in Table 1. The result shows that strong size-dependent melting temperatures for pure metal NPs are due to the increased fraction of loosely bounded surface atoms at reduced dimension. From Table 1, we also find that the melting point of core/shell structured Ti@Al NPs is remarkably lower than that of corresponding size pure Ti NPs. Evidently, the lowered melting point can be attributed to the influence of Al shell. From Figs. 3 and 4, one can see that the Al shell melts prior to the Ti core. Therefore, it is naturally explained that, after melting of shell, the melted Al atoms motivate those Ti atoms initially located in the outer layer of the core to move more easily, leading to the lower melting temperature of the Ti core, which has been verified by Fig. 3.

3.2. Solidification simulation

The solidification simulation continues after heating the five different Ti@Al NPs. As a representative, NP2 has also been used to exhibit the thermal evolution of Ti@Al NPs under the continuous cooling process.

Reference [35] reported that there are some difficulties in the amorphization process of TiAl alloys using the conventional rapid quenching technique. To validate this conclusion, first of all we calculate the potential energies for three cooling rates of NP2, with the results shown in Fig. 5. For the slow cooling rate of 0.15 K/ps, simulation produces an abrupt decrease in the potential energy, around 761 K, which is a clear indication of the formation of crystal structures. The crystallizing phenomenon can be identified by the distinct decrease in the potential energy. In this case, the crystallizing temperature Tc is determined as 761 K. For the cooling rate of 6 K/ps, the abrupt decrease of the potential is also found in Fig. 5, indicating that the crystal structure is formed. References [24] and [29] pointed out that at this cooling rate, a glassy phase has been formed. This supports the conclusion in Ref. [35]. The crystallizing temperature Tc for the cooling rate of 6 K/ps is 612 K, which is different from the cooling rate of 0.15 K/ps. So we conclude that the crystallizing temperature is largely dependent on the cooling rate, which is in good agreement with Ref. [36]. The crystallizing temperature Tc of five different Ti@Al NPs for the cooling rate of 0.15 K/ps is also listed in Table 2. We find that the crystallizing temperature Tc becomes higher with increasing total atom number, which shows a strong size-dependent crystallizing temperature. This result is different from the melting trend, which is a composition-dependent melting temperature. We should point out that the crystallizing temperature is largely dependent on the initial temperature and cooling rate, but the trend observed is reliable in the same condition. For the fast cooling rate of 12 K/ps, the potential energy exhibits a smooth linear decrease with the decrease of temperature, corresponding to a glassy phase formation.

Fig. 5. Potential energy profile of NP2 for three different cooling rates.
Table 2.

Crystallizing temperature Tc, and glass formation temperature Tg for different NPs.

.

Here, we calculate RDF to monitor particle structure evolutions during the simulation, as shown in Fig. 6 for two cooling cases. For the fast cooling rate of 12 K/ps, the RDF peaks increase with the decrease of temperature. The whole trend of RDF shows no major changes. This indicates that NP2 is from liquid phase to amorphous solid phase (the glass formation) during fast quenching. An empirical criterion for the onset of amorphous glass is given by Wendt and Abraham.[37] They defined RWA = gmin/gmax, where gmin and gmax denote the magnitude of the first minimum and the first maximum of RDF, respectively. RWA = 0.14 is the threshold value for the onset of the glass phase. On the basis of such a criterion, the calculated glass formation temperature Tg of five different Ti@Al NPs for the cooling rate of 12 K/ps is also listed in Table 2. We can easily see that the glass formation temperature also becomes higher with increasing total atom number. This conclusion also shows a strongly size-dependent glass formation temperature, which has much common with the analysis of the crystallizing temperature. For the slow cooling rate of 0.15 K/ps, RDF reveals features of transition from amorphous liquids to crystalline solids. Figure 5 has shown that the solidification point is clearly identified at 761 K by the abrupt decrease of potential energy. As shown in Fig. 6(b), the first peak becomes bigger and narrower with decreasing temperature, more peaks besides the primary peak start to emerge and grow below 600 K. These phenomena show that the structure of Ti–Al alloy has become more order and is crystal at low temperature (below 600 K). Here the detailed phase evolution during the quench process has been illustrated from the RDF profile. In addition, the calculated enthalpy change of the fast cooling rate of 12 K/ps is relatively lower than at the slow cooling rate of 0.15 K/ps. This reduces the crystallization driving force, thereby increasing the amorphous alloy forming ability. From the RDF profile, it is found that at solidification temperature, the rapid cooling rate makes the Al–Ti internal atomic do not have enough time to crystal and be frozen in the liquid atomic position, so as to form the amorphous structure.

Fig. 6. RDF of NP2 under different cooling rates: (a) cooling rate of 12 K/ps and (b) cooling rate of 0.15 K/ps.

In order to provide intuitive structure of the final quench product under different cooling rates, we present the final snapshot of the quenching as shown in Fig. 7. It is clear from the figure that the structure of the final product is different for three different cooling rates. Under the fast cooling rate of 12 K/ps, the final product is irregular, which shows that the atoms remain disorderly arranged after the solidification. When the cooling rate decreases to 6 K/ps, the final product is found in the crystalline order, but not very regular. We can conclude that the final product is not the glassy phase. For the slow cooling rate of 0.15 K/ps, it is easy to see the existence of crystalline ordering. This conclusion is in excellent agreement with the result discussed in Fig. 5. In Fig. 7, we also find that the icosahedron is formed for NP2 at the slow cooling rate of 0.15 K/ps. This is because the icosahedral structure optimizes the surface energy, so the icosahedral structure is more stable for nanoparticles. Nam et al.[38] have explained why the icosahedral structure is dominantly formed during the freezing of nanoparticles by using MD simulation.

Fig. 7. Snapshots of the final quench product of NP2 for three different cooling rates. Al atoms are colored in dark grey, while Ti atoms are in grey.
4. Conclusion

We have employed molecular dynamic simulations to investigate the thermal stabilities of Ti@Al NPs with different sizes and components under continuous heating and cooling. The analyses of potential energy and specific heat during the heating simulation have revealed that the effect of component on the melting temperature can be found. We have found that the liquid shell and solid core coexist for core/shell Ti@Al NPs during heating process, which would raise an interest for the catalytic properties of bimetallic core/shell NPs. The cooling rate significantly affects the final phase formation. A glass phase is formed for a fast cooling rate of 12 K/ps, while a crystal structure is formed for a slow cooling rate of 0.15 K/ps. The icosahedron structural is formed in the frozen 4366 Al–Ti atoms for the low cooling rate. The glass formation temperature and the crystallizing temperature can increase with the size of core/shell Ti@Al NPs.

Reference
1Djanarthany SViala J CBouix J 2001 Mater. Chem. Phys. 72 301
2Niu H ZKong F TChen Y YYang F 2011 J. Alloy. Comp. 509 10179
3Forouzanmehr NKarimzadeh FEnayati M H 2009 J. Alloy. Comp. 471 93
4Vaucher SStir MIshizaki KCatala-Civera J MNicula R 2011 Thermochim. Acta 522 151
5Sun YVajpai S KAmeyama KMa C 2014 J. Alloy. Comp. 585 734
6Liu TZhang T WZhu MQin C G 2012 J. Nanopart. Res. 14 738
7Sienkiewicz JKuroda SMolak R MMurakami HAraki HTakamori SKurzydlowski K J 2014 Intermetallics 49 57
8Nogorani F SAshrafizadeh FSaatchi A 2012 Surf. Coat. Tech. 210 97
9Garbacz HPouquet J MGarcía-Lecina EDíaz-Fuentes MWieciński PMartin R HWierzchoń TKurzydlowski K J 2011 Surf. Coat. Tech. 205 4433
10Ryu J RMoon K IILee K S 2000 J. Alloy. Comp. 296 157
11Patselov AGreenberg BGladkovskii SLavrikov RBorodin E 2012 AASRI Procedia 3 107
12Li X WSun H FFang W BDing Y F 2011 Trans. Nonferrous Met. Soc. China 21 s338
13Zhou KWang H PWei B 2012 Chem. Phys. Lett. 521 52
14Pei Q XLu CFu M W 2004 J. Phys.: Condens. Matter 16 4203
15Xie Z CGao T HGuo X TQin X MXie Q 2014 J. Non-Cryst. Solid. 394 16
16Kiselev S PZhirov E V 2014 Intermetallics 49 106
17Koizumi YYoshiya MSugihara AMinamino Y 2011 Philos. Mag. 91 3685
18Tan X QChen JZhi WBrown J 2010 Physica B 405 3543
19Levchenko E VEvteev A VLöwisch G GBelova I VMurch G E 2012 Intermetallics 22 193
20Levchenko E VEvteev A VLorscheider TBelova I VMurch G E 2013 Comp. Mater. Sci. 79 316
21Moon K IILee K S 1999 J. Alloy. Compd. 291 312
22Bhattacharya PBellon PAverback R SHales S J 2004 J. Alloy. Compd. 368 187
23Shu S LQiu FTong C ZShan X NJiang Q C 2014 J. Alloy. Copmd. 617 302
24Song PWen D 2010 J. Phys. Chem. C 114 8688
25Wen Y HHuang RLi CZhu Z ZSun S G 2012 J. Mater. Chem. 22 7380
26Cheng DHou M 2010 Eur. Phys. J. B 74 379
27Huang RWen Y HShao G FZhu Z ZSun S G 2013 J. Phys. Chem. C 117 6896
28Huang RWen Y HShao G FSun S G 2013 J. Phys. Chem. C 117 4278
29Cheng X LZhang J PZhang HZhao F 2013 J. Appl. Phys. 114 084310
30Plimpton S 1995 J. Comput. Phys. 117 1
31Zope R RMishin Y 2003 Phys. Rev. B 68 024102
32Pezold J vonDick AFriák MNeugebauer J 2010 Phys. Rev. B 81 094203
33Qi YCagin TJohnson W LGoddard W A 2001 J. Chem. Phys. 115 385
34Cao BStarace A KJudd O HJarrold M F 2009 J. Am. Chem. Soc. 131 2446
35Kambara MUenishi KKobayashi K F 2000 J. Mater. Sci. 35 2897
36Li G JWang QCao Y ZLü XLi D GHe J C2011Acta Phys. Sin.60093601(in Chinese)
37Wendt H RAbraham F F 1978 Phys. Rev. Lett. 41 1244
38Nam H SHwang N MYu B DYoom J K 2002 Phys. Rev. Lett. 89 275502