Cite this Article
Zuo Yanlei, Wei Xiaofeng, Zhou Kainan, Zeng Xiaoming, Su Jingqin, Jiao Zhihong, Xie Na, Wu Zhaohui. Enhanced laser-induced plasma channels in air. Chinese Physics B, 2016, 25(3): 035203  
Permissions
Enhanced laser-induced plasma channels in air
Zuo Yanlei1, 2, 3, Wei Xiaofeng1, 2, 3, Zhou Kainan1, 2, 3, Zeng Xiaoming1, 2, 3, Su Jingqin1, 2, 3, Jiao Zhihong1, Xie Na1, 2, Wu Zhaohui1, †,
Laser Fusion Research Center, China Academy of Engineering Physics, Mianyang 621900, China
Science and Technology on Plasma Physics Laboratory, Mianyang 621900, China
IFSA Collaborative Innovation Center, Shanghai Jiao Tong University, Shanghai 200240, China

 

† Corresponding author. E-mail: wuzhaohui20050@163.com

Project supported by the Development Foundation of the Chinese Academy of Engineering Physics (Grant Nos. 2012A0401019 and 2013A0401019).

Abstract
Abstract

Plasma is a significant medium in high-energy density physics since it can hardly be damaged. For some applications such as plasma based backward Raman amplification (BRA), uniform high-density and large-scale plasma channels are required. In the previous experiment, the plasma transverse diameter and density are 50–200 μm and 1–2 × 1019 cm−3, here we enhance them to 0.8 mm and 8 × 1019 cm−3, respectively. Moreover, the gradient plasma is investigated in our experiment. A proper plasma gradient can be obtained with suitable pulse energy and delay. The experimental results are useful for plasma physics and nonlinear optics.

PACS: 52.50.Dg;52.50.Jm;52.38.Fz;52.70.Kz;
Keyword:plasma channel;laser-induced plasma;plasma measurement;plasma optics;
1. Introduction

Plasma plays an important role in high-energy density physics since it can hardly be damaged by high energy radiation. Additionally, the Langmuir wave in plasma has been paid more and more attention in recent years because it can strongly interact with the laser field. Currently, plasma is widely used in plasma wave guiding,[1,2] high harmonic generation,[3,4] wakefield acceleration,[5] and resonant Raman amplification.[6–9] However, as a fluid medium, it is difficult to be formed and shaped. An excellent plasma channel is usually a key element for obtaining a good experimental result.

Large-scale and high-density plasma channels are required for experiments. For instance, plasma based backward Raman amplification (BRA) has been experimentally proved to be effective in the amplifications of both picosecond pulses [10] and femtosecond pulses.[11–15] The results of the Princeton experiment indicated that the peak seed intensity was amplified to 4 × 1016 W/cm2 from 1.3 × 1012 W/cm2.[14] The total power, however, was still far from reaching terawatt (1012 W) because of the micrometer interaction spot.[14,15] To enlarge the interaction aperture, high-power pump pulses and large-scale plasma channels are required. Now kilo-joule, picosecond pump pulses generated with the chirped pulse amplification (CPA) technique can supply millimeter-scale pump spots to BRA. Therefore, millimeter-scale plasma channels are required. The plasma wavebreaking, which can terminate the resonant interaction when it happens, is another effect limiting the output power of BRA in plasma. Additionally, many nonlinear effects will be dramatic when the plasma wave is close to the wavebreaking. Thus, higher-density plasma with a higher wavebreaking threshold is necessary to enhance the output seed intensity.[16]

The gradient plasma can also be applied in wakefield acceleration and BRA. On one hand, it might provide a gradient wakefield for particle acceleration. On the other, in BRA, it can compensate the frequency detuning caused by the pulse chirp. Having high intensities, chirped pulses are commonly used in plasma based BRA, but the pulse chirp can also cause frequency detuning. The gradient plasma with a well designed frequency gradient can minimize the frequency detuning. Additionally, it is proposed to filter out the noise in BRA.[17] Hence, a gradient plasma channel is necessary for these applications.

The plasma channel can be created by discharge and laser sparks in microcapillaries or gases.[18] Among these methods, the laser-induced plasma in gases is widely used in experiments. The reported aperture and density of the plasma channels are 50–200 μm and 1–2 × 1019 cm−3,[10,14] respectively. In this paper, we dramatically enhance the scale and the density of the plasma channel created by laser sparks in the air. Besides, the gradient plasma channel is investigated in the experiment. A proper gradient can be obtained by adjusting the pulse energy and time delay.

2. Experimental setup

The experimental setup to produce plasma by laser sparks is illustrated in Fig. 1. A 1053 nm Nd:glass laser pulse with a beam diameter of 6 mm and a full-width at half-maximum (FWHM) duration of 3 ns is taken as the source of both the laser spark and the diagnostic light. The polarization of the pulse is kept at the vertical direction in the experiment (the results are little influenced if the pulse is horizontally polarized). A small part of the pulse is frequency doubled to 2ω by an LBO crystal. Then the 1053-nm pulse and the 2ω pulse are separated by a 45° dichroic mirror R1, which has high reflectance at 527 nm and high transparency at 1053 nm. After a delay, the 2ω pulse is equally split into two portions, one of which vertically passes through the plasma channel, while the other propagates in the air. These two portions then are recombined to generate interferometric fringes. A 4f optical imaging system consisting of 3 focusing lenses (L1, L2, and L3, with focal lengths of 2 m, 0.4 m, and 0.4 m, respectively) enlarges the interferograms and clearly delivers them onto a camera. The rest 1053 nm pulse carrying more than 95% of the initial energy is focused by L4 in air to generate plasma. The pulse energy ranges from 20 mJ to 300 mJ. After the beam is focused to a spot of size 10–30 μm by the lenses (f = 50–150 mm), the pulse intensity is on the order of 1013 W/cm2, which is high enough for multiphoton ionization.

Fig. 1. Experimental setup to produce plasma in the air by laser sparks. SHG is the abbreviation for the second harmonic generation.

After the interferograms are obtained by the CCD camera, the phase distribution of the plasma can be unwrapped from them. The method of Fourier transform is applied to filter out the irrelevant information, and Branch-cut is used for phase unwrapping. Then, because the phases are still line integrals, the Abel inversion is taken to deduce the real phase distribution for a radially symmetrical object. Among several numerical methods of Able inversion, the Fourier–Hankel transform is chosen here because it can provide higher inversion accuracies than the other methods.[19–21]

To obtain a higher plasma density, a high-intensity pulse is usually demanded. To enlarge the transverse plasma scale, two methods are commonly adopted. Firstly, in general, the plasma scale can be enlarged by a large focused spot, which requires long-focus lenses. However, this method is limited by the formation of periodic structures which have been reported in several references.[22–24] Therefore, a suitable focus length should be set. Secondly, the transverse plasma scale can also be enlarged by the plasma expansion. With a measuring delay of tens of nanoseconds, the plasma expands, and the scale increases swiftly. The expanding velocity representing the plasma temperature can be increased by heating the plasma (using high-energy pulses). Therefore, a higher pulse energy and a longer delay are beneficial. Above all, we try to produce demanded plasma via changing the focus length, the pulse energy and delay.

3. Experimental result
3.1. High-density plasma

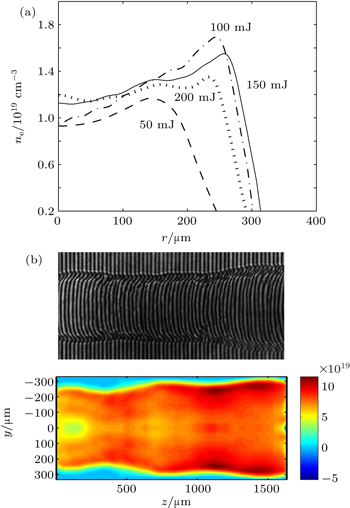
A high pulse intensity is required to produce a relatively high-density plasma. Therefore, a short-focus lens of f = 50 mm was firstly chosen in the experiment. Additionally, since the plasma density decreases as the plasma expands, a short delay is favorable. However, in the experiment, the interferograms are not regular until a delay of 30 ns, which implies that the plasma is not uniform enough. The interferograms captured by the CCD camera at the delay of 30 ns are shown in Fig. 2(a), indicating that the plasma scale increases both radially and axially with the pulse energy.

The plasma density derived from the phase is shown in Fig. 2(b). An average plasma density of ∼7 × 1019 cm−3 is achieved when the pulse energy is above 50 mJ. This density is higher than the atom density of 5.4 × 1019 cm−3, implying that more than one electron are ionized per atom. After that, although the pulse energy continuously increases, the plasma density does not rise dramatically, showing a saturation of the electron number in the initial ionized zone (the radius of the plasma channel is about 100 μm at the delay of 3 ns). Another phenomenon observed in the experiment is that the longitudinal gradient aggravates as the pulse energy increases. It will be specially discussed later.

Fig. 2. (a) Interferograms and (b) radial distributions (averaged over z) of the plasma channel obtained with different pulse energies (delay = 30 ns, f = 50 mm).

As shown in Fig. 2(a), the radial plasma scales are not consistent at different axial positions, and the maximum axial length is no more than 1.5 mm. To obtain longer and more uniform plasma channels, long-focus lenses were employed for the experiment. A quite uniform plasma channel with a total axial length of about 2 mm is well formed at the focus length of f = 100 mm. When the focus length is longer, however, the periodic structures become serious. From Fig. 3, it can be seen that these structures start to destroy the plasma channel at the focus length of f = 150 mm. Therefore, the lens of f = 100 mm was finally chosen for the experiment.

Fig. 3. Interferograms of plasma obtained with lenses of f = 100 mm and f = 150 mm (delay) = 30 ns, E = 100 mJ).

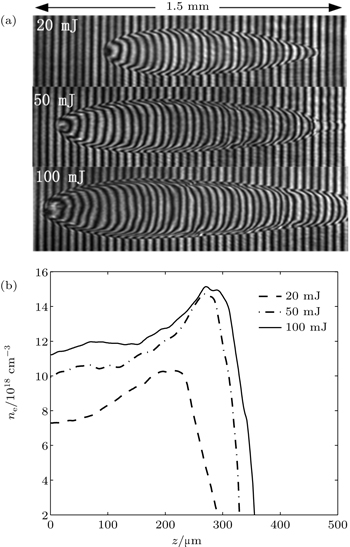
It should be noted that the plasma density will decrease when a long-focus lens is applied due to a lower laser intensity at the focused spot. However, this drawback can be overcome by using a higher pulse energy, as shown in Fig. 4. An average plasma density of 8.2 × 1019 m−3 and a traverse radius over 250 μm are obtained at the pulse energy of 150 mJ. The two-dimensional (2D) interferogram and density distribution of the plasma channel are displayed in Fig. 4(b), showing an axial length of 1.6 mm and a quite uniform diameter of ∼ 200 μm in this case.

Fig. 4. (a) Density distributions and (b) interferogram of high-density uniform plasma channel (delay = 30 ns, f = 100 mm). In panel (b), E = 150 mJ.
3.2. Large-scale plasma

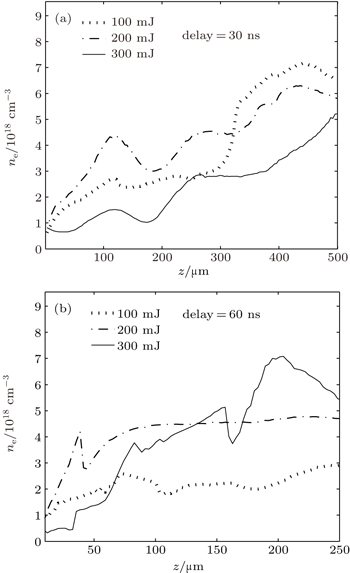
In general, a large focused spot enhances the plasma scale. However, as mentioned in Section 2, this method is limited by the periodic structures. Therefore, instead of this approach, we increased the delay and the pulse energy to enlarge the plasma scale, and the measured results are given in Fig. 5(a). As the delay varies from 30 ns to 60 ns, the plasma channel expands while the density decreases. The plasma channel is more homogeneous with a longer delay due to the plasma diffusion. The plasma scale is further enhanced by raising the pulse energy. It can be seen from Fig. 5(b) that a plasma channel with a transverse diameter of ∼0.8 mm is obtained at the pulse energy of 250 mJ and the delay of 60 ns. It is quite uniform with an axial length of 1.5 mm and a plasma density of 4.5 × 1019 cm−3.

Fig. 5. (a) Density distributions and (b) interferogram of large-scale uniform plasma channel (delay) = 60 ns, f = 100 (mm). In panel (b), E = 250 mJ.
3.3. Gradient plasma

As the pulse propagates in the air, its intensity decreases gradually. Therefore, the plasma channel is not longitudinally uniform. The plasma gradient is found in the axial direction. However, when the pulse energy is very low, the plasma channel is seriously impacted by the periodic structures, as seen in Fig. 6. These interferograms cannot correctly describe the plasma gradient. The plasma gradient as a function of the pulse energy over 100 mJ is shown in Fig. 7. It increases with the pulse energy, which can be explained by the formula δne ∝ Iδz, where I is the absorbed pulse intensity. According to the results of linear fitting, the plasma density gradient ranges from 0.85 × 1020 cm−4 to 3.3 × 1020 cm−4 as the pulse energy increases. Conversely, a much smaller plasma gradient is found at the delay of 60 ns, as shown in Fig. 7(b). Due to the plasma diffusion, the plasma channel becomes more uniform, thereby the gradient is reduced. It is less than 0.8 × 1020 cm−4 (0.1–0.8 × 1020 cm−4) even with a high-energy pulse. Although the gradient can cause plasma nonuniformity, it can be used to filter out the noise of BRA by the mechanism of frequency detuning.[17] By changing the pulse energy and delay, a plasma channel with a proper gradient is capable of enhancing the transfer efficiency of the resonant interaction.

Fig. 6. Interferograms of the plasma channel at low energies (f = 100 mm, delay = 30 ns).
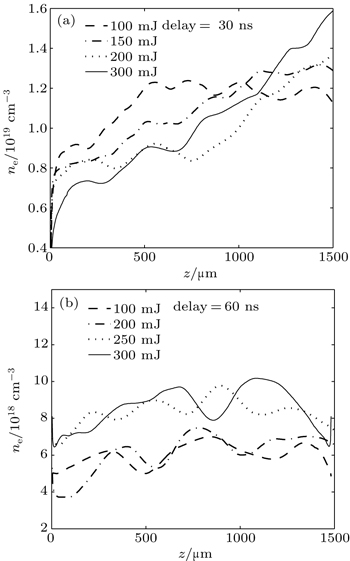Fig. 7. Axial distributions (averaged over r) of the plasma density at various delays ((a) delay = 30 ns, (b) delay = 60 ns) and pulse energies (f = 100 mm).

Another issue that should be noted is the axial edge of the plasma channel. The significant inverse bremsstrahlung and seed dispersion caused by inhomogeneous plasma may impede the resonant Raman interaction.[25] The left edges are not given in the text because they become irregular due to the periodic structures. The right axial edges (at the pulse front) are shown in Fig. 8. Although the edges are not as sharp as the transverse ones in Fig. 5, the edged gradient is much larger than that of the plasma channel. As seen in Fig. 8, the edged gradient does not directly depend on the pulse energy but on the plasma density. At the same delay, a sharper axial plasma edge is caused by a higher plasma density. Compared with Fig. 8(a), the edged length becomes shorter while the plasma density becomes lower in Fig. 8(b), indicating that the edged gradient is not dramatically impacted by the delay. To reduce the axial edged instability, the plasma channel can be created in a gas jet. If the length of the jet (along the direction of the laser pulse) is shorter than the plasma length, the axial edges might be eliminated.

Fig. 8. Axial edges (averaged over r) of the plasma density at the pulse front at various delays ((a) delay = 30 ns, (b) delay = 60 ns) and pulse energies (f = 100 mm).
4. Summary

The features of plasma channels induced by laser sparks in the air have been investigated by experiments. By changing the pulse energy, the focus length, and the delay, we obtained high-density, large-scale, and gradient plasma channels, respectively. The plasma density was enhanced to 8 × 1019 cm−3; the maximum transverse diameter was 0.8 mm, and the plasma gradient was varied between 0.1 × 1020 cm−4 and 4 × 1020 cm−4 by changing the pulse energy and delay.

According to the experimental results, the following conclusions can be made. Firstly, at the pulse intensity of ∼1013 W/cm2, more than one electron were ionized per atom. A plasma channel with a density of ∼ 1020 cm−3 and a transverse diameter of several hundred micrometers could be created by laser sparks in the air. Secondly, in general, the plasma scale can be enlarged by long-focus lenses, long delays, and high-energy pulses. However, the focus length should not be too long to avoid periodic structures. Therefore, the plasma scale was primarily enlarged by the plasma expansion. With this method, millimeter-diameter and quite uniform plasma channels were produced. Thirdly, the gradient plasma was found in the experiment. The gradient was a function of the pulse energy and delay. This gradient plasma could be used to filter out the noise in BRA by the effect of frequency detuning.

Several methods can be developed to further enhance the plasma density and scale. From the experiment results, it can been seen that the plasma density can be effectively increased by increasing the pulse energy and the gas pressure. However, the plasma gradient can also be aggravated, thereby the plasma uniformity might be influenced. The 1053-nm pulse was applied here to create plasma channels. A short-wavelength pulse can promote the electron ionization, however, the periodic structure becomes more serious when a 527 nm pulse is used.[23] The periodic structure is a significant issue when a large-focal-spot laser spark is applied to enlarge the plasma scale. Because of the plasma diffusion, a well-designed delay is helpful to obtain a uniform and large-scale plasma channel. However, the plasma density will decrease correspondingly, limiting the enlarged plasma diameter to not far from 1 mm. According to the theoretical simulation, this plasma channel can satisfy the demand of BRA in plasma for petawatt (1015 W) pulses.[26] For exawatt–zattawatt (1018−1021 W) laser pulses, however, it is still far from satisfactory (centimeter-diameter channels[27]). Above of all, in the regime of multiphoton ionization, the periodic structure is the main reason that prevents plasma uniform and scale. Despite the fact that the mechanism of this phenomenon has still not been fully identified, it is commonly agreed that it is due to the plasma generated by the pulse front impacting the propagation of the pulse body and tail.[23,28] Therefore, the periodic structure will become more dramatic with a longer pulse duration. It is necessary to employ an ultrashort pulse with a peak intensity over 1014 W/cm2 to drive the ionization to the tunneling regime. In this case, the outer-shell electrons can be fully ionized within several optical cycles (such as H2). Thus, both the plasma inhomogeneity and the periodic structure might be effectively suppressed.

Reference
1Ehrlich YCohen CZigler AKrall JSprangle SEsarey E1996Phys. Rev. Lett.774486
2Pai C HLin M WHa L CTsou S TChu H HLin J YChen S Y 2008 Phys. Rev. Lett. 101 065005
3Shkolnikov P LLago AKaplan A E1994Phys. Rev. A774461
4Kuo C CPai C HLin M WLee K HLin J YWang JChen S Y 2007 Phys. Rev. Lett. 98 033901
5Litos MAdli EAn WClarke C IClayton C ECorde SDelahaye J PEngland R JFisher A SFrederico JGessner SGreen S ZHogan M JJoshi CLu WMarsh K AMori W BMuggli PVafaei-Najafabadi NWalz DWhite GWu ZYakimenko VYocky G 2014 Nature 515 92
6Malkin V MShvets GFisch N J 1999 Phys. Rev. Lett. 82 4448
7Fisch N JMalkin V M 2003 Phys. Plasmas. 10 2056
8Wang H YHuang Z Q 2005 Chin. Phys. 14 2560
9Wu Z HWei X FZuo Y LLiu L QZhang Z MLi MZhou Y LSu J Q 2015 Chin. Phys. B 24 014211
10Ping YKirwood R KWang T LClark D SWilks S CMeezan NBerger R L 2009 Phys. Plasmas. 16 123113
11Ping YGeltner ISuckewer2003Phys. Rev. E67016401
12Ping YCheng W FSuckewer SClark D SFisch N J 2004 Phys. Rev. Lett. 92 175007
13Cheng W FAvitzour YPing YSuckewer S 2005 Phys. Rev. Lett. 94 045003
14Ren JCheng WLi SSuckwer S 2007 Nature Physics 3 732
15Ren JLi SMorozov ASuckewer SYampolsky N AMalkin V M 2008 Phys. Plasmas 15 056702
16Yampolsky N AFisch N J2011Phys. Plasmas1805611
17Malkin V MShvets GFisch N J 2000 Phys. Plsamas. 7 2232
18Ping YMorozov AFisch N JSuckewer S 2002 Phys. Plasmas 9 4756
19Buie M JPender J T PHowlloway J PVincent TVentzek P L GBrake M L 1996 J. Quant. Spectrosc. Radiat. Transf. 55 231
20lvarez RPender AHowlloway M C 2002 Spectrochim. Acta 57 1665
21Shuiliang MHongming GLin W2008Appl. Optics91350
22Durfee C GLynch JMilchbeerg H M1995Phys. Plasmas512368
23Ping YGeltner ISuckewer SPhys. Plasmas84174
24Ping Y2002Soft X-ray Lasers and Raman Amplification in PlasmasPh. D. thesis, Princeton University
25Toroker ZMalkin V MBalakin A AFraiman G M Fisch N J 2012 Phys. Plasmas 19 083110
26Trines R M G MFiúza FBingham RFonseca R ASilva L OCairns R ANorreys P A 2011 Nat. Phys. 7 87
27Mourou G AFisch N JMalkin V MToroker ZKhazanov E ASergeev A MTajima TGarrec B L 2012 Opt. Commun. 285 720
28Margolin L Ya 1999 Quantum Electron. 29 246