† Corresponding author. E-mail:
Project supported by the National Science Instruments Major Project of China (Grant No. 2012YQ130125), the National Natural Science Foundation of China (Grant Nos. 11405159, 11375161, and 11174259), and the Science and Technology on Plasma Physics Laboratory at CAEP (Grant No. 9140C680302130C68242).
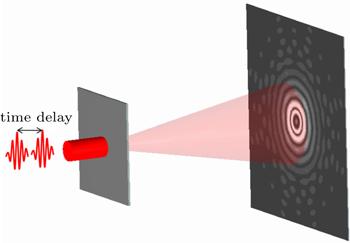
The spatio-temporal characterization of an isolated attosecond pulse is investigated theoretically in a two-color field. Our results show that a few-cycle isolated attosecond pulse with the center wavelength of 16 nm can be generated effectively by adding a weak controlling field. Using the split and delay units, the isolated attosecond pulse can be split to the two same ones, and then single-pinhole diffractive patterns of the two pulses with different delays can be achieved. The diffractive patterns depend severely on the periods of the attosecond pulses, which can be helpful to obtain temporal information of the coherent sources.
With the development of laser technique, the duration of ultrashort intense laser pulse falls continually and has approached two optical cycles, which resulted in a breakthrough of isolated attosecond pulse generation.[1,2] The attoseceond pulse has great potential for controlling and detecting the electronic dynamics of the substance at atom level, such as inner-shell electronic relaxation and ionization by optical tunnelling.[3] Nowadays, various schemes for the attosecond pulse generation, such as Thomson Scattering,[4,5] stimulated Raman scattering,[6] and high-order harmonic generation (HHG)[7–11] have been explored. The HHG is the only experimental way to generate the attosecond pulses.[12–14] The physical mechanism of HHG can be well understood by the three-step model.[15] First, an electron of atoms tunnels through the barrier formed by the laser field and the Coulomb potential, then it oscillates in the continuum, finally it may return to the parent ion, emitting a harmonic photon with maximal energy up to Ip + 3.17Up, where Ip is the ionization potential and 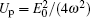
The study for characterizing the attosecond pulse is at the early stage.[21–23] Due to the lack of nonlinear phenomena in the soft x-ray region for the correlation measurement and the low intensity of attosecond pulses, the atto-correlation scheme is still a challenge.[24–27] The duration measurement of the attosecond pulse is usually performed by the cross-correlation techniques, which only obtains the information of the duration. With the develop of the two-color field schemes and the phase-matching schemes, the yields of the attosecond pulse have improved a lot, which means that it is possible to obtain other temporal information, such as optical periods of attosecond pulse.
In this paper, we investigate that the spatio-temporal characterization of an isolated attosecond pulse in a two-color field. Our results present that a few-cycle isolated attosecond pulse with the center wavelength of 16 nm can be obtained effectively by adding a weak controlling field. Using the split and delay units, the few-cycle attosecond pulse can be split into two same ones,[28] and then single-pinhole diffractive patterns of the two pulses with different delays can be achieved. The diffraction patterns depend severely on the periods of the attosecond pulses, which can be used to temporal diagnostics of the coherent sources.
In the theoretical model of HHG, the single-atom response (SAR) to the laser field and the collective response in macroscopic gas to high harmonic fields are both taken into account. The single-atom response is calculated with SFA,[29] and the light propagation equations of the laser and HHG are solved in cylindrical coordinate separately in order to simulate the collective response of macroscopic gas.[30]
To simulate the diffraction of the two same attosecond pulse with different delays, we describe two arbitrary attosecond pulses with time delay as[31]
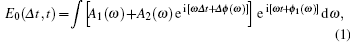
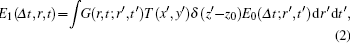
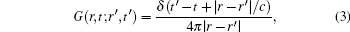
For example, an ideal attosecond pulse with the center wavelength of 20 nm is divided into two same pulses. Figure
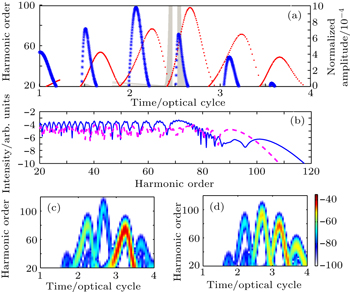
In this work, the two-color laser pulse is synthesized by a 5-fs linearly polarized fundamental field with a wavelength of 800 nm and a 5-fs linearly polarized controlling field with a wavelength of 400 nm. The peak intensity of the fundamental and control fields is 6 × 1014 W/cm2 and 2.4 × 1013 W/cm2, respectively. The electric field of the two-color laser pulse is expressed by
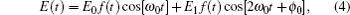
The HHG process in the two-color field is well understood by the semiclassical three-step model and the ADK model which is shown in Fig.
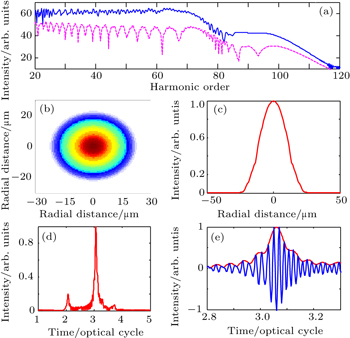
The harmonic spectrum can be further modulated by account of the collective response. The short and long paths have different response in macroscopic gas, which can lead to one quantum path. The nonadiabatic three-dimensional propagation model is performed in a 0.5-mm-long gas target with a density of 1.37 × 1018 cm−3. To optimize the spatial profile of the high-order harmonic spectrum, the driving and controlling pulses foci are placed 2 mm and 0 mm before the gas target, and the beam waists of the driving and controlling pulses are 25 μm and 15 μm, respectively. The other parameters are the same as those in Fig.
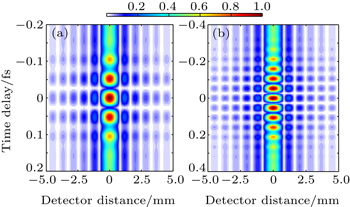
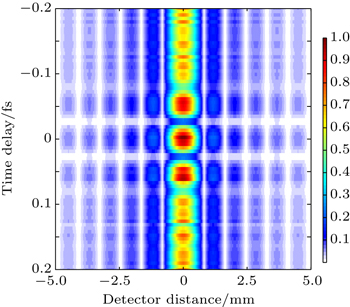
The wavelength of the few-cycle isolated pulse is 16 nm, belonging to the soft x-ray regime. Therefore the optical elements for achieving single-pinhole diffraction of the attosecond pulses have the special optical requirements. Fortunately, to provide the replica attosecond pulses and vary the delay of those pulses, the optical elements such as a beam splitter and pulse delay units have been developed and applied. By using a split optical component, the five-cycle isolated attosecond pulse obtained by the synthesized field is divided into the same two pulses, the delay between the two attosecond pulses can be adjusted by the delay units. The diffraction patterns of the attosecond pulses with different periods are shown in Fig.
In this paper, the spatio-temporal characterization of an isolated attosecond pulse in a two-color laser field is investigated. The results present that a few-cycle isolated attosecond pulse with the center wavelength of 16 nm can be obtained effectively by adding a weak control field, and the intensity of the attosecond pulse is enhance by one order. Using a split unit, the isolated attosecond pulse can be split into the two same ones, and the delay of the two attosecond pulses can be varied by delay units. The single-pinhole diffraction patterns of the two pulses can be achieved by adjusting different delays. The diffraction patterns depend severely on the periods of the attosecond pulses, which can be used in temporal diagnostics of the coherent sources.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 |