Cite this Article
Lin Peng, Ma Jian, Lo Siuming. Discrete element crowd model for pedestrian evacuation through an exit. Chinese Physics B, 2016, 25(3): 034501  
Permissions
Discrete element crowd model for pedestrian evacuation through an exit
Lin Peng1, Ma Jian2, †, , Lo Siuming3
Department of Fire Safety Engineering, Southwest Jiaotong University, Chengdu 610031, China
School of Transportation and Logistics, National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
Department of Civil and Architectural Engineering, City University of Hong Kong, Tat Chee Avenue, Kowloon, Hong Kong

 

† Corresponding author. E-mail: majian@mail.ustc.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 71473207, 51178445, and 71103148), the Research Grant Council, Government of Hong Kong, China (Grant No. CityU119011), and the Fundamental Research Funds for the Central Universities, China (Grant Nos. 2682014CX103 and 2682014RC05).

Abstract
Abstract

A series of accidents caused by crowds within the last decades evoked a lot of scientific interest in modeling the movement of pedestrian crowds. Based on the discrete element method, a granular dynamic model, in which the human body is simplified as a self-driven sphere, is proposed to simulate the characteristics of crowd flow through an exit. In this model, the repulsive force among people is considered to have an anisotropic feature, and the physical contact force due to body deformation is quantified by the Hertz contact model. The movement of the human body is simulated by applying the second Newton’s law. The crowd flow through an exit at different desired velocities is studied and simulation results indicated that crowd flow exhibits three distinct states, i.e., smooth state, transition state and phase separation state. In the simulation, the clogging phenomenon occurs more easily when the desired velocity is high and the exit may as a result be totally blocked at a desired velocity of 1.6 m/s or above, leading to faster-to-frozen effect.

PACS: 45.70.Mg;05.65.+b;07.05.Tp;
Keyword:crowd evacuation;discrete element method;anisotropic social force;contact force;
1. Introduction

The evacuation system of buildings provides the last defense line for occupants within a fire emergency. In recent decades, the evacuation becomes more and more challenging for modern buildings, which are characterized by the increases in size, height and occupancy as well as complexity of layout and evacuation routes. Usually, a modern building would accommodate a large number of people. When a huge amount of people gather together, the over-congested crowd substantially reduces the exit flow rate and may trigger potential disasters such as trampling and stampede, which have resulted in many deaths and injuries in previous decades.[1] Building codes in different countries worldwide stipulate the requirements on the design of the egress system, whose performance in a real fire scenario is difficult to assess. The design of an egress system for complex buildings is a formidable task. With the advancement of simulation techniques and the power of computers, researchers have developed dozens of evacuation models, such as Exodus,[2] SGEM,[3] SFF,[4] etc., to evaluate the effectiveness of the escape system or evacuation plan in buildings.

These models can deepen our understanding and may help in preventing accidents due to overcrowding. Thus this research topic has attracted attention from physicists and sociologists in recent years. Generally speaking, pedestrian movement models can be classified into different categories such as macroscopic continuum models,[5,6] force-based models,[7–9] and cellular automaton (CA) models.[10–12] Macroscopic models describe the pedestrian movement at a high level of aggregation as fluid flow,[5,6] which can optimize the overall evacuation network,[13] whilst microscopic models describe the behavior of each individual and their interactions in detail. The movement of people in microscopic models is simplified as a kind of self-driven particle[7,8,14–16] in which the driving force is not external, but from each particle itself. Helbing et al. proposed a pedestrian model to quantitatively explain the behavior of panicked individuals.[7,15,16] They created a generalized force model using Newton’s formula in which force equals pedestrian mass multiplied by its corresponding acceleration. They found “faster is slower effect” in a panicked evacuation. Over several decades, studies specifically looking at panic behavior in fires have consistently shown that non-adaptive and irrational behaviors are actually a rare occurrence.[17–19] After a study of the crowd incident in the love parade on 24th July 2010, in Duisberg, Germany, Helbing et al.[20] concluded that there was no sign of panic in the crowd flow during the incident. A special crowd movement pattern, i.e., crowd turbulence, as found in Ref. [21], would be the cause of the loss of 21 lives in the tragedy. In Refs. [8] and [14], based on suitable video recordings of interactive pedestrian motion and improved tracking software, the authors proposed an evolutionary optimization algorithm to determine optimal parameter specifications for the social force model. The calibrated model is then applied in exploring large-scale pedestrian and evacuation simulations including pilgrimage and urban environments. They found the phenomena of intermittent flows and stop-and-go wave in crowd flow at extremely high densities.[22] Stop-and-go wave is an onset followed by a highly irregular motion of crowd, i.e., the occurrence of crowd turbulence.[20–22] This crowd dynamics is dangerous and it may cause people to fall down. It is noted that the reaction of pedestrians to what happens in front of them is much stronger than to what happens behind them and a centrifugal social force model[23,24] was proposed by taking into account the distance between pedestrians as well as their relative velocities. Recently, researchers modified the social force model and analyzed the faster-is-slower phenomenon by performing animal experiments.[25,26] The social-force model has also been used to investigate the effect of complex building architecture on the uncoordinated crowd motion during urgent evacuation.[27] In particular, how the room door size, the size of the main exit, the desired speed, and the friction coefficient affect the evacuation time and under what circumstances the evacuation efficiency improves.

Discrete element method (DEM) is a numerical method for computing the motion and effect of a large number of particles.[1,28–30] The forces acting on each particle are calculated and force balance is integrated explicitly and acceleration velocity, velocity and the coordinate at each time step is deduced accordingly by applying the second Newton’s law. Normally, soft-sphere is used where particles are allowed to slightly overlap. Lin et al.[1] proposed a granular dynamic method to study the egress pattern of evacuees in a densely populated enclosed space. A DEM-technique-based crowd dynamics model, i.e., CrowdDMX had also been developed by Langston.[31] They further investigated the behavior of subgroups in crowd dynamics.[32] An agent-based algorithm-based DEM algorithm has been incorporated in FDS-Evac[33] and it was further extended to model agents’ behavior in counter-flow situations.[34] However, the faster-is-slower effect, as observed in Helbing’s original social force model, is not reported in the CrowdDMX and FDS-Evac despite both the models having adopted the social force model as a basic model.

The objective of this paper is to study how the desired velocity affects the throughput of the exit by using the discrete element method. The paper is structured as follows. In Section 2, we first introduce the original social force model, then discuss its limitations and lastly make some revisions accordingly. We will detail the formulation of the proposed model based on the theory of granular dynamic. In Section 3, a parametric study will be conducted. The characteristics of crowd flow at different desired velocities and the flow rates out of the exit are then investigated. Section 4 presents the conclusions.

2. Discrete element crowd movement model
2.1. Social force model

In the original social force model,[7,15,16] the movement of people is quantified by the following equations:

where mi is the mass of pedestrian i, vi(t) is the velocity of pedestrian i at time t, vi0 is the desired velocity, is the desired direction of movement, ε is the reaction time and ε = 0.5 s is suggested,[35] is the sum of the contact forces with walls or boundaries, is the sum force among people and it includes two parts. One part is the social force among people to maintain a comfortable distance and the other part is the contacted force due to physical body deformation. The social force is the repulsive force as represented as fij = A exp[(rij − dij)/B], dij is the separation distance of two persons and rij = ri + rj is the sum of the radius of the two persons. The parameters A and B are introduced to describe the strength and spatial extent of the force, respectively. Here, A = 2000 N and B = 0.08 m were proposed. The contact force includes the normal contact force Fn and the tangential contact force Fτ, and they can be represented as Fn = kn(rij − dij)n and Fτ = kτ(rij − dij)Δvττ, respectively. Here, n is in the normal direction and τ is in the tangential direction, Δvτ is the tangential velocity difference, kn and kτ are normal contact coefficient and tangential contact coefficient, respectively, kn = 1.2 × 105 kg·s−2 and kτ = 2.4 × 105 kg·m−1·s−1 are proposed.

2.2. Discussion on the social force model

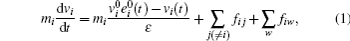
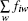
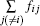
In the social force model, a person receives repulsive forces from all the people around him so as to keep a comfortable distance to these people. That is to say, distance is an important factor in the social force model. However in the centrifugal force model,[23,24] another important factor, the relative velocity was also taken into account. Recently, it was found that the reaction of pedestrians to what happens in front of them is much stronger than what happens behind them.[8] Thus, a so-called anisotropic social force model is proposed in Ref. [32]. In this model,

where ϕij is the angle between the direction of the person i feeling the force and the direction to the person j. The parameter λi represents the anisotropy of the social force, λi = 1 corresponds to the original social force model and λi < 1 represents the force in front of the person is larger than the force behind, A = 2000 N and B = 0.08 m are implemented in FDS-Evac and CrowdDMX, A = 2000 N denotes that the repulsive force is 2000 N when two persons contact but with no physical body deformation, meaning the distance between them is zero. It should be noticed that this force could lead to an acceleration speed of 25 m·s−2 for a 80 kg person. Even a world 100 m dash champion like Usain Bolt cannot achieve such a high acceleration speed (his estimated acceleration speed is about 3.09 m·s−2.[36]) Therefore, the adopted parameters in the original social force model and the revised anisotropic social force model are questionable.

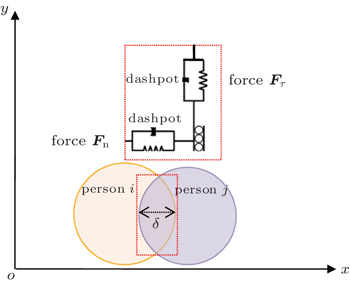
Furthermore, the contact force within the human body is an important factor to describe the forces within the human body when they are physically contacted. In the original social force model, as implemented in FDS-Evac and CrowdDMX, the human body is assumed to be an elastic object and the contacted forces are represented by Hooke’s law where the compressive force of the human body is linearly dependent on the distance they are pressed. For two spherical particles, the normal push-back force for two overlapping particles is a non-linear function of the overlapped distance but is proportional to the overlapped area as illustrated in the Hertz contact model.[28,30] Therefore, the contact force in the social force model is over-simplified.

2.3. Discrete element crowd model

In DEM simulation, a granular material is modeled based on a finite number of discrete, semi-rigid spheres interacting by means of contact or non-contact forces, and the translational and rotational motions of every single particle in a considered system are described by Newton’s laws of motion.[37] In situations such as massive crowd evacuation, each individual does whatever he can to escape, e.g., rushing, pushing, or twisting, to get out the exit as quickly as possible. As a result, translational and rotational movements should both be considered. For simplicity, spherical particles used in the present study are limited to represent granular pedestrian system.

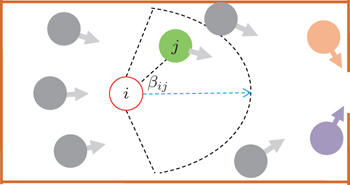
For the translational movement, we assume that the movement of people is restricted in two-dimensional space, xoy, while the position in z direction keeps constant. The basic translational motion equations of the human body are similar to the ones used in social force, as detailed in former sections. We noticed the animal dynamics reported in Ref. [25] and as a consequence assume that the people in front of a person i pose a much higher social impact on him than the persons behind him when there is no physical body contact. That is to say, the social force has an anisotropic feature, as shown in Fig. 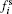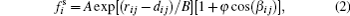1. The anisotropic social force is expressed as

where the parameter A is anisotropic social force when the separation distance is zero and B is a parameter related to variation of anisotropic force against separation distance, βij is the angle between the direction of the person i feeling the force and the direction to the person j, the parameter φ represents the anisotropy of the social force, and φ < 1 represents the force in front of the person is larger than the force behind.

Fig. 1. Scheme of anisotropy social forces posed on a person.

When there is physical body contact, the contact force is an important factor to describe the forces among human bodies. The most used contact model is the Hertz contact model[28] as shown schematically in Fig. 2. The normal push-back force for two overlapping particles is proportional to the area of overlap of the two particles, and is thus a non-linear function of the overlapped distance. As shown in Fig. 2, person i is in contact with person j, the normal contact force Fn, acting on person j, is given by the sum of the normal spring force and normal damping force as

The tangential component of the contact force Fτ, is similarly given by the sums of the tangential spring force and the tangential damping force as

where δ is the overlap distance of two persons if they are physically contacted, i.e., rij > dij and δ = rij − dij, kn is the elastic constant for normal contact, kn = 2E/3(1 + σ)(1 − σ), in which σ is the Poisson ratio, E is the Young’s modulus, kτ is the elastic constant for tangential contact, kτ = 2E/(1 + σ)(2 − σ), γn is the damping constant for normal contact, γτ is the viscoelastic damping constant for tangential contact, mij is the effective mass of two persons and mij = mimj/(mi + mj), δτ is the tangential displacement vector between two persons, vn is the velocity difference in normal direction, δvτ is tangential component of the relative velocity of the two persons. The magnitude of the tangential force is limited by the Coulomb frictional limit, where the particles begin to slide over each other.

Fig. 2. The Hertz contact model.

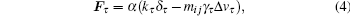
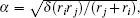
The rotational movement of the human body is restricted in z directions only and the rotations in directions x and y are set to be zero.

where Ii represents the moment of inertia for pedestrian i, ωi denotes the angular velocity, ∑Mi is the total rolling moment and can be calculated by

where is the vector connecting the center of the mass of particle i with its contact point with particle j and F is the sum of all tangential contact forces at contact points. The rolling moment is a result of tangential contact force fi. Considering when a body is standing on an uneven surface in a state of rest, a critical force, i.e., the static friction force Fs, must be overcome to set him in motion. This friction force is roughly proportional to the normal force Fn, i.e., Fs = μFn, where μ is the coefficient of static friction. Kinetic friction Fk is the resisting force which acts on a body after the force of static friction has been overcome. Based on Coulomb’s experiment, the kinetic friction is similar to static friction and the coefficient of kinetic fraction is approximately equal to that of static friction, therefore, the dynamic friction in the human body is similar to the static friction in the proposed model. That is to say, both static friction and kinetic friction among pedestrians are considered in the present model. If Fτ > Fs, the particle can move and the sum of contact forces should be F = Fτ + Fk.

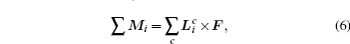
The algorithm of translational crowd movement based on the DEM includes the following steps.

Step 1 Creation of the human particles randomly and initialization of all parameters.

Step 2 Calculation of the contact forces, the self-driven force, and the social force.

Step 3 Summing up all forces ∑ F(t).

Step 4 Based on Taylor expansion and Velocity Verlet integration, the position and velocity at each time step can be expressed as

This step includes the following four sub-steps.

Step 5 Continue the steps from 2–5 until the end of the simulation.

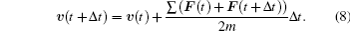
Similarly, the rotational crowd movement can also be realized following similar steps by replacing force, location, speed, and acceleration items with moment, orientation, angular speed, and angular acceleration items respectively.

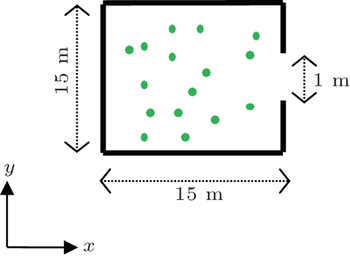
3. Simulation results and discussion

A number of simulations have been performed for the evacuation of people through an exit. The room is 15 m×15 m and has an outlet of 1 m wide as shown in Fig. 3. The coordinate of the room is x ∈ [0,15] in x direction, y ∈ [0,15] in y direction and z ∈ [0,0.38] in z direction. An outlet of 1-m wide is at the center, i.e., y ∈ [7,8]. The diameter of the human body is 0.6±0.1 m. At the beginning of the simulation, people are randomly distributed in the room and then they will initiate the movement by the self-driven force at their desired velocity. The key input parameters are shown in Table 1. It should be admitted that the present model introduced more parameters than the social force model, thus due to the lack of experimental data, calibration of these parameters needs further research work. Thus the model parameters are referenced from data in granular flow theory considering pedestrian and granular flow similarities.

Fig. 3. The schematic layout of the crowd flow through an exit.
Table 1.

Key input parameters in the simulations.

.
3.1. Parametric analysis

First, we simulate an evacuation scenario of 100 people getting out of a 1-m-wide door at a desired velocity (DV) of 1 m/s and simulation results are shown in Fig. 4. With A = 200 N, the leaving time of 100 persons is around 170 s, equivalent to a flow rate of 0.6 s−1·m−1. With A = 300 N, the leaving time is around 120 s, equivalent to a flow rate of 0.833 s−1·m−1, which is basically consistent with the flow rate of 0.92 s−1·m−1 as observed by Fruin in arena evacuation.[38] Further increasing the value of A from 300 N to 500 N barely affects the flow rate out of the exit. Therefore, A = 300 N, B = 0.05 m, φ = 0.3 are implemented in subsequent simulations and as a result the repulsive force is 300 N when two persons are at zero distance.

Fig. 4. Evacuation process of 100 people getting out of a 1-m-wide door at a desired velocity of 1 m/s.

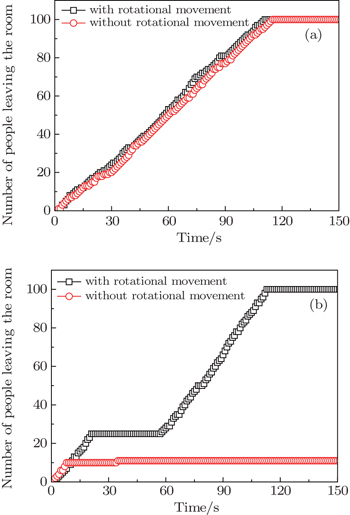
To determine the effect of rotation in the present model, more simulations are conducted by deactivating the rotational Eq. (5). Simulation results are shown in Fig. 5. From this figure, we can see when people move with a relatively low desired velocity (here, we choose 1.0 m/s as a representing case, as shown in Fig. 5(a)), the evacuation processes are basically the same as those with rotational equation. However, in contrast, when people move with a higher desired velocity and no rotational movement is considered, as shown in Fig. 5(b), the clogging possibility increases. Once clogged, the pedestrian crowds could barely recover to fluent evacuation process. The comparative study showed that the rotational movement of the human body, to some extent, can prevent the formation of clogging near the exit.

Fig. 5. The evacuation process of 100 people getting out of a 1-m-wide door at desired velocities of (a) 1 m/s and (b) 2 m/s.
3.2. Effect of desired velocity

The clearance time of the occupants within the room is further studied for scenarios with 200 and 300 persons, which are equivalent to an initial density of 0.88 m−2 and 1.33 m−2, respectively. Other key input parameters are shown in Table 1.

For 200 people in the room, we show in Fig. 6 typical evacuation snapshots. The clearance time at different desired velocities is shown in Fig. 7. From this figure, we can find that the clearance time is approximately 340 s at a desired velocity of 0.6 m/s and it reduced to 210 s when the desired velocity increases to 1.0 m/s. With the desired velocity increased from 0.6 m/s to 1.0 m/s, the clearance time is reduced continuously from 340 s to 210 s. By further increasing the desired velocity from 1.0 m/s to 1.8 m/s, the clearance time goes up and down but the average clearance time is close to 220 s. With higher desired velocity of 1.8 m/s, the exit is blocked by evacuees and no one gets out within the next 2 min, i.e., clogging occurs. That means the crowd at a desired velocity of 1.8 m/s or higher could lead to total blockage of the exit.

Fig. 6. Snapshots of the crowd evacuation at the time of (a) 0 s, (b) 30 s, (c) 60 s, and (d) 120 s.
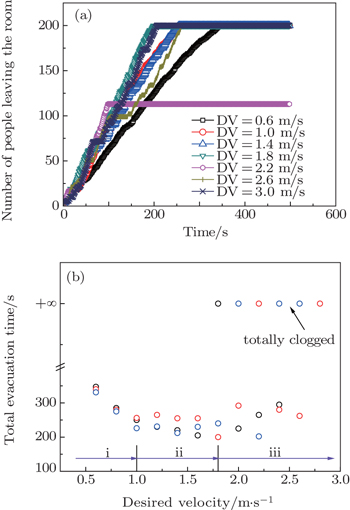Fig. 7. The leaving process (a) and clearance time (b) of 200 persons at different desired velocities. In panel (b), different colors mean different runs of the simulation.

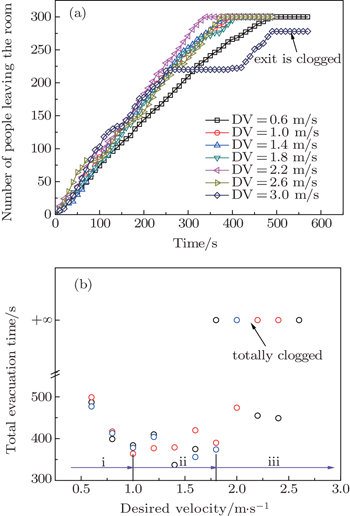
Further study with 300 persons is conducted and the results are shown in Fig. 8. As can be found in Fig. 8, the results are consistent with that of 200 people. In summary, the relationship between the clearance time and the desired velocity can be classified into three states as follows.

Fig. 8. The leaving process (a) and clearance time (b) of 300 persons at different desired velocities. In panel (b), different colors mean different runs of the simulation.
3.3. Exit flow rate

The exit flow rate is measured at small temporal intervals (10 s) to investigate the flow rate at different desired velocities. Examples of typical results are presented in Fig. 9. In this figure, the temporary interruptions of the flow are caused by arches that block the exit, while the downward spikes indicate the temporary blockage of the exit. When a group of particles flow through a silo in granular flow, the interactions among the particles may lead to the spontaneous development of clogs, as found in experimental granular flow observations.[39–41] The intermittent flow was also observed in the crowd flow through an exit as shown in Figs. 8 and 9(a).

Fig. 9. The flow rates of 100 people (a) and 300 people (b) getting out of the exit at different desired velocities.

In the social force model, we know that a special phenomenon named “faster-is-slower” is observed. The quickest leaving time of 200 persons is around 150 s at a desired velocity of 1.5 m/s and the leaving time increases to 200 s at a desired velocity of 5 m/s.[16] Here, in Fig. 9, we can find that for a desired velocity of 0.6 m/s, the flow rate varies from 0.4 s−1 to 0.6 s−1. At a desired velocity of 1–1.2 m/s, the flow rate varies from 0.3 s−1 to 1.3 s−1. At a desired velocity of 1.6 m/s or above, the flow rate varies from 0 to 1.6 s−1. Although the overall tendency of the evacuation times is consistent with the “faster-is-slower" phenomenon, we can observe a totally jammed phase in our simulation even if the desired velocity is not so large.

The average flow rate of people getting out of the exit is further investigated with different initial number of people to be evacuated. The results are summarized in Fig. 10. From this figure we can see that the relationship between the flow rate and the desired velocity can also be classified into three states. i) The smooth state, in which flow rate increases with the increase of the desired velocity from 0.6 m/s to 1 m/s. ii) The transition state, in which flow rate fluctuates from 0.7 s−1 to 0.95 s−1 with the desired velocity increased from 1.0 m/s to 1.6 m/s. The impatience of the crowd neither reduces the flow rate, nor improves the efficiency of the exit. The flow rate stays at an average of 0.82 s−1. iii) Phase separation state, in which flow rate fluctuates greatly from 1.22 s−1 to zero when the desired velocity of crowd is greater than 1.6 m/s. The crowd movement at the exit would become frozen if there is a desperate crowd at a desired velocity of greater than 1.6 m/s, which leads to the faster-to-frozen effect. Meanwhile, in Fig. 8, phase transition is observed where the system transforms from a state of free movement to a state of total jam or blockage at the exit and the throughput decreases dramatically near the transition state when the degree of impatience increases.

Fig. 10. The flow rates of the crowd getting out of the exit at different desired velocities.
4. Concluding remarks

In the original social force model, the parameters for the social force are questionable and the contact force due to body deformation is over-simplified. Thus in the present study, we built a model for crowd flow through an exit by adopting the theory of granular dynamic. In the proposed model, the human body is treated as a granular particle and the dynamical movement of people is studied by applying the second Newton’s law. The Hertz contact model is incorporated to describe the contact forces on the human body when they are physically contacted. The friction force among particles is also considered, and finally a revised anisotropic discrete element crowd model is formalized. Within this model, the effect of DV was investigated. It was assumed that a larger desired velocity means a higher degree of intention of people wanting to get out of the room. The clearance time and flow rate of people getting out of a room at different desired velocities were investigated. The relationship between the clearance time/flow rate and the desired velocity exhibits three distinct states as follows.

Our simulations show that the clogging phenomenon occurs more easily at the exit if all people still try to get out at a desired velocity irrespective of the net distance/space available. The competitiveness of the crowd cannot improve the flow rate but only adds to its fluctuation and the over-competitiveness of the crowd could lead to the clogging at the exit, i.e., faster-to-frozen effect.

It should be noted that the current model only considers the rotation of the human body due to external contact force. In fact, people are self-driven particles and they can provide internal rotational force so as to twist or rotate their body if they are jammed at the exit. It is believed that the internal rotational force could reduce the clogging possibility. It should also be noticed that in the current model, the evacuation process with only one exit was considered, whilst two or more exits is generally provided in the reality. By introducing a novel potential field such as the one proposed in Refs. [42] and [43], multi-exit evacuation will be further studied in the future.

Reference
1Lin PLo S MYuen K K 2007 Fire Safety J. 42 377
2Galea E RGalparsoro J M P 1994 Fire Safety J. 22 341
3Lo S MFang ZLin PZhi G S 2004 Fire Safety J. 39 169
4Wang X LGuo WZheng X P 2015 Chin. Phys. B 24 070504
5Hughes R L 2002 Trans. Res. Part B 36 507
6Dogbe C 2012 J. Math. Anal. Appl. 387 512
7Helbing DMolnár P 1995 Phys. Rev. E 51 4282
8Johansson AHelbing DShukla P K 2007 Adv. Complex Systems 10 271
9Zhang LYue HLi MWang SMi X Y 2015 Acta Phys. Sin. 64 060505 (in Chinese)
10Tanimoto JHagishima ATanaka Y 2010 Physica A 389 5611
11Ma JSong W GLiao G X 2010 Chin. Phys. B 19 128901
12Ding NZhang HChen TPeter B L 2015 Chin. Phys. B 24 068801
13Lin PLo S MHuang H CYuen K K 2008 Fire Safety J. 43 282
14Johansson AHelbing D2010Pedestrian and Evacuation Dynamics200820321410.1007/978-3-642-04504-2_15
15Helbing DFarkas IVicsek T 2000 Phys. Rev. Lett. 84 1240
16Helbing DFarkas IVicsek T 2000 Nature 407 487
17Fahy R FProulx G2009NRCC-51384
18Keating J P1982Fire J.7657
19Quarantelli E L1957Sociology and Social Research4141
20Helbing DMukerji P 2012 EPJ Data Science 1 7
21Ma JSong W GLo S MFang Z M2013Journal of Statistical Mechanics: Theory and ExperimentP02028
22Yu W JJohansson A 2007 Phys. Rev. E 76 046105
23Chraibi MSeyfried A 2010 Phys. Rev. E 82 046111
24Yu W JChen RDong L YDai S Q 2005 Phys. Rev. E 72 026112
25Zuriguel IParisi D RHidalgo R CLozano CJanda AGago P APeralta J PFerrer L MPugnaloni L AClément EMaza D 2014 Sci. Rep. 4 7324
26Soria S AJosens RParisi D R 2012 Safety Sci. 50 1584
27Ha VLykotrafitis G 2012 Physica A 391 2740
28Hirshfeld DRadzyner YRapaort D C 1997 Phys. Rev. E 56 4404
29Robbins C RMckee S2001Aeronautical J.105323
30Hu M BJiang RWu Q S 2013 Chin. Phys. B 22 066301
31Langston P AMasling RAsmar B N 2006 Safety Sci. 44 395
32Singh HArter RDodd LLangston PLester EDrury J 2009 Appl. Math. Model. 33 4408
33Korhonen THostikka S2009FDS+Evac Technical Reference and User’s Guide VTT Technical Research Centre of Finland
34Heliövaara SKorhonen THostikka SEhtamo H 2012 Building and Environment 48 89
35Ma JSong W GFang Z MLo S MLiao G X 2010 Building and Environment 45 2160
36Allian R2012Maximum Acceleration in the 100 m Dash
37Parisi D RGilmana MMoldovan H 2009 Physica A 388 3600
38Fruin J J1987Pedestrian Planning and Design(Elevator World Educational Services Division, Mobile, AL)
39Yang G CLiu Q YHu M BJiang RWu Q S 2014 Phys. Lett. A 378 1281
40Lozano CJanda AGarcimartiín AMaza DZuriguel I 2012 Phys. Rev. E 86 031306
41Hu M BLiu Q YJiang RHou MWu Q S 2015 Phys. Rev. E 91 022206
42Zhang PJian X XWong S CChoi K 2012 Phys. Rev. E 85 021119
43Xiong TZhang PWong S CShu C WZhang M P 2011 Chin. Phys. Lett. 28 108901