Surface plasmon polaritons (SPPs) are the surface electromagnetic (EM) waves propagating along a dielectric–metal interface at the optical frequencies.^[1] Owing to the unique properties of guiding and localizing electromagnetic (EM) waves into sub-wavelength scales, the SPPs have attracted increasing attention in the past decade.^[2,3] The intrinsic properties associated with the SPPs have enabled potential applications of designing highly integrated circuits and devices in the areas of optoelectronics, material science, and biosensing. There is also increased interest to extend the unique properties of the SPPs to lower frequencies for the exploration of various integrated circuits and devices in the terahertz (THz) and microwave regimes. However, as a metal resembles a perfect electric conductor (PEC) in these low frequency regimes, the SPPs cannot be supported on smooth metal surfaces.

Recently, plenty of works have demonstrated that the highly confined surface EM waves, named spoof SPPs or designer SPPs, could be supported by plasmonic metamaterials, which usually consist of a textured metal surface with sub-wavelength scaled grooves or dimples.^[4–12] The surface plasmon frequency and the SPP-like dispersion property of the spoof SPPs could be scaled down to the THz or microwave region by using these plasmonic metamaterials. However, all these plasmonic metamaterials with non-planar geometry primarily rely on a three-dimensional (3D) structure of the sub-wavelength scaled geometry on metal surfaces, making them inconvenient to be fabricated and integrated with other existing THz or microwave circuitries. More recently, an ultra-thin plasmonic metamaterial has been proposed to support spoof SPPs.^[13–16] Due to its flexible and planar property, such ultra-thin plasmonic metamaterial paves a way for developing versatile surface wave integrated devices or circuits at lower bands, especially at the THz region.

Spoof SPPs based devices, such as ultra-thin surface plasmonic bandpass filters, were also reported,^[17–19] which show excellent filtering characteristics such as low loss, wide band, and high square ratio. However, the upper stopband of the reported ultra-wideband filter is very narrow,^[17] which is also exhibited in other ultra-wideband microstrip line filter designs.^[20] Thereafter, more effort is still needed to design a bandpass filter with an extremely wide upper stopband that is highly demanded in practical applications for effective suppression of the undesired noise signal.

In this paper, by detailed study of the condition or operating frequency region of the single mode propagation of spoof SPPs on a symmetric ultra-thin plasmonic structure, we propose a spoof SPPs based wide passband filter with an extremely wide upper stopband. It is designed by combining the cut-off of the spoof SPPs with a transmission zero created through a pair of shunt stepped-impedance stubs at the lower frequency band. A flaring ground is also employed in the connecting microstrip line to feed the proposed filter. Both simulation and measurement results on S-parameters have demonstrated the emergence of an extremely wide upper stopband above the desired wide passband.

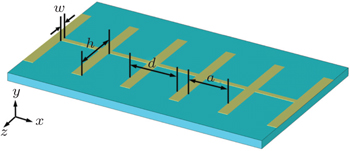
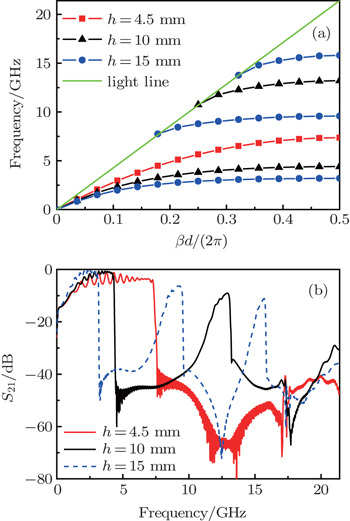
The symmetric spoof SPPs structure is composed of a thin metal strip on the top of a dielectric substrate with a thickness of 0.813 mm, relative dielectric constant of 3.55, and loss tangent of 0.003. Herein, the two sides of the metallic strip are symmetrically corrugated by a one-dimensional array of grooves with depth h, width a, lattices constant d, and central line width w, as schematically illustrated in Fig. 1. It has been previously confirmed that the symmetric spoof SPPs structure can support both even and odd propagating modes.^[15] In this work, we will utilize the propagation properties of even modes in the symmetric spoof SPPs structure. In our analysis, the eigen-mode solver of the commercial full-wave software, CST microwave studio, is used to numerically calculate the dispersion relation of the symmetric spoof SPPs structure. Different groove depths h are chosen, while the other parameters d, a, and w are set as 7 mm, 6 mm, and 0.3 mm, respectively. The obtained dispersion curves are plotted in Fig. 2(a). We can see that the higher order modes manifest themself within a certain frequency band when h > d. This is similar to that of the single side spoof SPPs structure.^[21] The dispersion curve of the single side spoof SPPs structure can be calculated by the formula

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Geometry of an ultra-thin symmetric spoof SPPs waveguide on a dielectric substrate.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Dispersion relation of spoof SPPs for different groove depths h. The parameters d, a, and w are set as 7.0 mm, 6.0 mm, and 0.3 mm, respectively. (b) The corresponding transmission spectra.

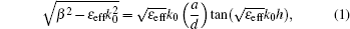
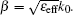
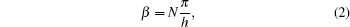
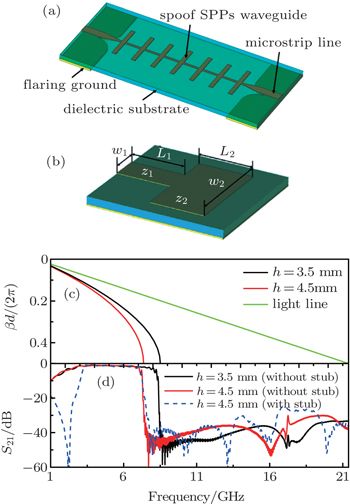
In order to achieve an efficient single-mode transmission, we adopt the microstrip line with a flaring ground as a bridge or transition from the SMA connectors to the spoof SPPs waveguide, as shown in Fig. 3(a). The function of this flaring ground is mainly to convert the microstrip-line mode to the coplanar-waveguide mode and then to the desired spoof SPPs mode.^[15,16] The parameters h, d, a, and w are set as 4.5 mm, 7 mm, 6 mm, and 0.3 mm, respectively. The simulated results are shown by the red solid line in Fig. 3(d). We can see that an efficient transmission band is achieved. The reflection S₁₁ is lower than −10 dB and the transmission S₂₁ is higher than −1.2 dB in a wide frequency region from 2.7 GHz to 6.7 GHz. The transmission spectrum of spoof SPPs corresponds to that of a low pass filter with an extremely wide upper stopband. Furthermore, the cut off frequency may be easily adjusted by the groove depth. The cut off frequency is increased to 8.39 GHz when choosing a smaller h = 3.5 mm, as shown in Fig. 3(d). Meanwhile, the cut off frequency agrees with the asymptotic frequency of the corresponding dispersion curve in Fig. 3(c).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Schematic diagram of the symmetric spoof SPPs structure with input and output microstrip line sections. (b) Schematic diagram of a shunt stepped-impedance resonator. (c) Calculated dispersion curve. (d) Simulated results of a spoof-SPPs based lowpass filter and the bandpass filter with stepped-impedance resonators added.

Based on the previous transmission spectrum of the spoof SPPs, a wide bandpass filter with an extremely wide upper stopband can be further obtained by introducing a transmission zero at the low frequency band. In our study, a shunt stepped-impedance resonator is installed in the section of the microstrip line to acquire the transmission zero,^[22] which consists of two impedance sections as z₁ and z₂ with lengths L₁ and L₂, respectively, as shown in Fig. 3(b). The resonant frequency can be calculated by the formula

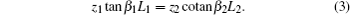
According to the previous analysis, we propose a bandpass filter structure as shown in Fig. 4(a). Considering the symmetry of the circuit, two pairs of stepped-impedance stubs are connected in shunt with two microstrip line transducers, respectively. These stubs are properly bent so as to miniaturize the entire filter circuit. The parameters h, d, a, w, L₁, w₁, L₂, and w₂ are set as 4.5 mm, 7 mm, 6 mm, 0.3 mm, 6.2 mm, 0.3 mm, 4.9 mm, and 4.5 mm, respectively. The first two resonant frequencies of the stepped-impedance resonators are calculated by Eq. (3) to be about 2.32 GHz and 13.89 GHz. The asymptotic frequency for the spoof SPPs structure is about 7.36 GHz. Therefore, the passband of the designed filter covers a range from 2.32 GHz to 7.36 GHz. The S parameters of the filter are first calculated and displayed in Fig. 4(d). The transmission zero is located at about 2.28 GHz in the low frequency band. The upper cut-off frequency is about 7.29 GHz with the transmission coefficient (S₂₁) of −10 dB. These frequencies are roughly coincident with the analytical ones. The result demonstrates excellent filtering characteristics, such as high out of band attenuation and high square ratio. The −3 dB bandwidth is about 3.9 GHz, covering a range from 3.24 GHz to 7.14 GHz. The upper stopband is extremely wide from 7.5 GHz to 22 GHz, which is fully determined by the forbidden region of the dispersion curve as shown in Fig. 3(c).

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Schematic diagram of the proposed bandpass filter structure. The front (b) and the back (c) side photographs of the fabricated prototype filter. (d) The simulated and measured S parameters of the filter.

Next, we fabricate a prototype sample and conduct microwave experiments to test the designed bandpass filter. A sample of the proposed filter is fabricated on a commercial print circuit board (PCB) dielectric substrate (Rogers 4003C, 0.813 mm), as shown in Figs. 4(b) and 4(c). The measured results are displayed as dashed lines in Fig. 4(d), which agree with the simulated ones, therefore verifying our previous analysis and the proposed design principle.

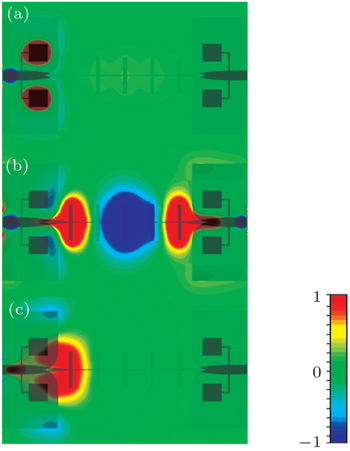
To get an insight into the filtering characteristics, the simulated y component of the electric field is plotted in Fig. 5 at several specific frequencies. We can find out that, owing to the introduction of the stepped-impedance resonators, the EM wave cannot be transmitted at around 2.28 GHz (resonant frequency), as illustrated in Fig. 5(a). The EM wave is also blocked at 9 GHz because the frequency is located in the band in which the wave cannot be supported by the spoof SPPs structure, as shown in Fig. 5(c). However, the wave can be well transmitted with little loss through the structure within the passband, for example at 5 GHz, as displayed in Fig. 5(b). We would like to remark that the frequency of either the lower or the upper end of the passband can be easily changed by altering the geometric parameters of the stepped-impedance resonator or the spoof SPPs structure.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The simulated electric field Ey distributions on the surface of the filter at the frequencies of (a) 2.28 GHz, (b) 5 GHz, and (c) 9 GHz, respectively.

We have extensively analyzed the guiding modes on a symmetric spoof SPPs structure. It shows that the mode number is mainly determined by the ratio between the groove depth and the lattice constant. Single-mode propagation may be supported by choosing a suitable ratio of these two parameters. Based on this property, a wide passband filter with a wide upper stopband has been designed at the microwave frequency range by introducing a transmission zero at the lower frequency band. To verify the predicted performance, we fabricated a prototype filter. The measured results of the filter validate the emergence of an extremely wide upper stopband above the desired passband. We believe that the proposed spoof SPPs filter is very promising for the exploration of other surface waveguide components or systems in both the microwave and terahertz bands.