Atoms, molecules, and clusters irradiated by a strong laser pulse of long wavelength can emit a coherent radiation at the frequency of integer multiples of that of the incident laser pulse.^[1–3] Such radiation is called high-order harmonic generation (HHG), and the mechanism of the atomic HHG can be well explained by a semi-classical three-step model,^[4] i.e., the bound electron firstly tunnels out through the barrier formed by the Coulomb potential and the laser field, then the ionized electron oscillates in the external field, and it has the possibility to recombine with its parent ion and finally emits a high-energy photon.

The high-order harmonic from molecules carries information about the molecular structure, so it can be used to realize the tomography of molecular orbitals,^[5] and this offers an opportunity to achieve ultrafast real-time imaging of the electron orbitals in a molecule. In order to reach this goal, the study on structural features of molecular harmonics and their relation with molecular electron orbitals becomes the current central issue. For the molecular system, the ionized electron may recombine with different ions, the harmonics from which may interfere with each other, thus leading to the minimum or maximum in the molecular harmonic spectra. Lein et al. firstly theoretically investigated this interference phenomenon, and found that the harmonic efficiencies in H₂ and are obviously suppressed at a certain frequency.^[6,7] The positions of the minima of the hydrogen molecule HHG spectra can be understood by a simple two-center model. The first experimental results about the interference effect were found in the CO₂ harmonic spectra, and the minimum of which can also be explained by the two-center model.^[8,9]

As for the experimentally measured harmonic spectra, the position of the harmonic interference minimum is mainly decided by the geometry structure of the molecule and the most contributive molecule orbital occupied with harmonic emission. Meanwhile, the orientation degree of molecules^[10,11] and the multi-path interference^[12] also have effects on the harmonic interference minimum during harmonic emission. In the theoretical study of this paper, we just consider the influence on the harmonic interference minimum for the ideally orientated molecule with specially occupied orbital selected. Certainly, for the correspondence with the experimental results, the hexapole method could be adopted to perform the state selection and improve the orientation degree of the molecules. As for theory, considering the condition of the specific molecule orientation degree and performing coherent superposition of harmonics from molecules with different orientations can also get results corresponding to experiments. In addition, we choose driven laser pulses with a relatively long wavelength and low intensity to make sure that a certain molecular orbital has obvious ionization and contributes the most to the harmonic emission, so the influences of low molecule orientation degree and multi-path interference on the harmonic interference minimum are reduced. However, for some molecules such as nitrogen, the harmonic spectrum minima predicted by the two-center model are different from those of the quantum results.^[13–15] In addition, this model cannot explain the multi-orbital contribution to the molecular HHG observed in the experiment.^[12] Despite the recent significant progress in HHG from molecules, the harmonic interference from different molecular orbitals remains an open question. Recently, Zhu et al. explained the interference minimum in the harmonic spectrum of the heteronuclear diatomic molecule by performing a phase analysis.^[16] In this paper, we develop the two-center model by modifying the initial phase difference between the double wave sources, and predict the interference minima in the HHG spectra of the linear molecules, which are well consistent with those from the strong-field approximation (SFA) calculation.^[17–19]

Considering each electron’s contribution to the harmonic generation from the multi-electron molecules, we investigate the molecular HHG by SFA. In the length gauge and the electric dipole approximation, the time-dependent dipole moment of the system is (the atomic units are used throughout the text unless otherwise specified)

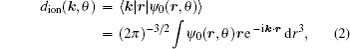
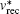
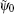
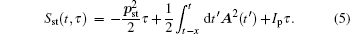
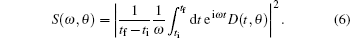
Firstly, we study the HHG from linear molecules nitrogen (N₂), acetylene (C₂H₂), and carbon monoxide (CO) irradiated by a linear polarized laser pulse. Here, the laser electric field is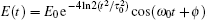. The corresponding central frequency, peak amplitude, duration (full width at half maximum), and carrier-envelope phase are ω₀ = 0.03507, E₀ = 0.1, τ₀ = 14.45 fs, and ϕ = 0, respectively. The wave functions of the HOMO and HOMO-1 molecular orbitals are calculated by the software GAMESS with the Hartree–Fock method. Figure 1 shows the variation with θ of the harmonic spectra generated from the HOMO and HOMO-1 orbitals of these molecules calculated by the SFA scheme. From this figure, one can see that for different molecular orbitals, the harmonic spectra all exist in minimum structures in intensity, which are marked by the red dotted lines. According to the two-center model, the wave packets of the colliding electrons reach two centers of the molecule in the HHG process, because their phase difference is odd times of π, there exists a destructive interference, which results in a dip structure in the molecular HHG spectrum. Moreover, the positions of the minimum structure can be predicted by the formula Rcosθ = (n − 1/2)λ, (n = 1,2,3,…), where R is the distance between the molecular nuclei and λ is the de Broglie wavelength of the recollision electron. By using this simple two-center model, the minimum positions of the molecular harmonic spectra can also be obtained, as shown by the white solid lines in Fig. 1. It can be found that the red dashed and white solid lines are consistent for the HOMO-1 orbital of N₂, the HOMO orbital of C₂H₂, and the HOMO-1 orbital of CO (Figs. 1(b), 1(c), and 1(f)). However, for N₂ HOMO, C₂H₂ HOMO-1, and CO HOMO orbitals (Figs. 1(a), 1(d), and 1(e)), the minimum positions predicted by the two-center model are apparently different from those obtained by SFA.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Harmonic emission spectra from different initial molecular orbitals: (a) HOMO of N2, (b) HOMO-1 of N2, (c) HOMO of C2H2, (d) HOMO-1 of C2H2, (e) HOMO of CO, and (f) HOMO-1 of CO. The white solid lines are the minimum positions from the two-center model.

According to the two-center model, the position of the interference minimum only depends on the nuclear distance and is not related to the initial shape of the molecular orbital. However, for the harmonic spectra from different initial orbitals of the same molecule, it is found that the minimal value distributions are not the same, as depicted by Fig. 1. To clearly understand the interference minimum, we analyze the time-frequency profile of the molecular harmonic emission using the wavelet transform of the time-dependent dipole moment.^[20–22] Taking the harmonic emission from the HOMO orbital of N₂ as an example, we show the time-frequency distribution of HHG in Fig. 2. It can be found that, in the periods of t₁ ≈ 14–17 and t₂ ≈ 53–55, the harmonic intensity is much lower, and the corresponding frequency of this minimum in intensity is about ω/ω₀ ≈ 154. This result is consistent with the dip position shown in Fig. 1(a).

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The frequency analysis of the total dipole moment of the HOMO orbital of N2. The red arrows indicate the positions of the destructive interference.

In order to clarify the disagreement in the dip structures between the two-center model and the SFA, we further investigate the harmonic emission from different atoms in the diatomic molecule. According to the SFA, the high-order harmonic structure depends on the transition dipole moments between the continuous state and the initial state. One can express the molecular orbital as the linear combination of atomic orbitals ψ₀ (r) = ψ₁ (r − R₁) + ψ₂ (r − R₂), where ψ₁, ψ₂ are the orbitals and R₁, R₂ are the nuclear positions of the two atoms. The internuclear distance of the diatomic molecule is R = |R₂ − R₁|. The recombination matrix element can be written as

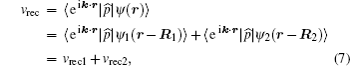
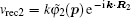
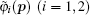
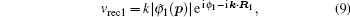
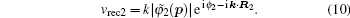
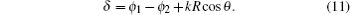
Then, we can calculate the dipole moment D₂₂(t) originated from the ionized electron from core (center) 2 recombining with core 2, and D₂₁(t) originated from the ionized electron from core 2 recombining with core 1. The time-dependent dipole moment D_all(t) can be obtained from the coherent superposition of D₂₁(t) and D₂₂(t). In the period t₁ ≈ 14–17, the amplitude of the electric field is positive, thus the potential that locates near core 2 is suppressed. The ionization from core 1 is difficult because it needs to overcome an additional potential barrier in the middle of the two cores. Thus the ionization from core 2 is dominant. Therefore, the time-dependent dipole moment D_all(t) can be taken as the whole dipole moment from N₂. Figures 3(a) and 3(b) present the above three dipole moments in the durations of 0–24 and 42–66, respectively. It can be seen that, in the periods of t₁ and t₂ (pink shaded box), the phases of the two time-dependent dipole moments D₂₁(t) and D₂₂(t) are opposite, which results in the small oscillation amplitude of the overall dipole moment, and the corresponding harmonic emission intensity is weak, as shown in Fig. 2. This indicates that the dip structure of the harmonic spectrum from the diatomic molecule can be explained by the interference process. If one can give a correct initial phase in the two-center model, the interference minimum predicted by the two-center model may agree well with that from the SFA calculation.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The variation of the dipole moments D22(t), D21(t), and Dall(t) with time in the durations of (a) 0–24 and (b) 42–60. The periods of the destructive interference are shown in the pink shadow boxes.

What causes the π phase difference between the two dipole moments D₂₂(t) and D₂₁(t)? To figure it out, we further consider the case of the electronic wave packet with the harmonic frequency 154 returning to the two N atoms, and find that the corresponding phase difference equals to 2π. It means that the phase difference π between D₂₂(t) and D₂₁(t) only originates from the two atoms as the interference centers, i.e., the initial two atomic wave functions of the N₂ HOMO orbitals exist in the phase difference π. It can also be seen from the HOMO orbital and two N atomic wave functions, as depicted in Fig. 4, which have opposite phases along the molecular axis, i.e., the initial phase difference between the two atomic orbitals is equal to π. Therefore, we modify the two-center model by considering the initial phase effect of the molecular orbitals. For the N₂ HOMO orbital (σ orbital), the interference minima of the harmonic spectrum can be predicted by the formula Rcosθ = (n − 1/2)λ, (n = 1,2,3,…). One can clearly see that the result from our modified two-center model agrees well with that from SFA. This also indicates that the interference minimum of the HHG spectrum is dominated by the initial phase of the two atomic wave functions because of the symmetry of the molecular orbital.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The orbital wave functions of (a) ψN2, (b) ψ1N, and (c) ψ2N.

In order to confirm this conclusion, we analyze the interference minima in the HHG spectra from other linear molecular orbitals. Figure 5 shows the wave functions of the N₂ HOMO-1, C₂H₂ HOMO-1, CO HOMO, and CO HOMO-1 orbitals, the corresponding two-center wave functions of which are also presented. For σ orbitals, such as the C₂H₂ HOMO-1 (Fig. 5(c)) and CO HOMO (Fig. 5(d)) orbitals, the symmetries of the two-center orbitals are opposite along the molecular axis, and the initial phase differences are set as π; for π orbitals, such as the N₂ HOMO-1 (Fig. 5(a)), C₂H₂ HOMO (Fig. 5(b)), and CO HOMO-1 (Fig. 5(e)) orbitals, the symmetries of the two-center orbitals are the same along the molecular axis, and we set the initial phase differences as zero. By using the improved two-center model, the interference minima of the harmonic spectra are marked as the red dotted lines in Fig. 1. It can be seen that the minimum positions by this model are consistent with those from SFA. These results demonstrate that the modified two-center model can well predict the interference minima for the linear molecules. Because the probability distribution of the O atomic orbital has little contribution to the molecular orbital, and the harmonic from the ionized electron recombing with it is too small, it leads to a weak interference effect. As a result, there is no obvious minimum in the harmonic spectrum from the CO molecular orbital. As for molecules with asymmetric orbitals, the inherent phase difference of the two centers is unnecessary to be integral multiples of π. For example, in this manuscript, the CO molecule involved has different orbital shapes for the C and the O atom cores, and the inherent phase difference is not exactly but almost π; details can be found in Refs. [16] and [23].

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The wave functions of (a) N2 HOMO-1, (b) C2H2 HOMO, (c) C2H2 HOMO-1, (d) CO HOMO, and (e) CO HOMO-1 orbitals. The low panels show the wave functions of the corresponding two-center orbitals.

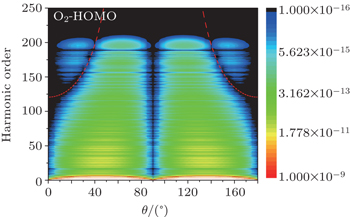
The improved two-center model also works well for the anti-bonding orbitals of the linear molecules. Here, we take the O₂ HOMO orbital as an example. Figure 6 shows the O₂ molecular and the O atomic orbitals. It can be noticed that the distributions of the two atomic wave functions along the molecular axis are anti-symmetry. Thus, the initial phase difference between the two atomic orbitals can be set as π in the modified two-center model. The interference minima of the O₂ molecular harmonic spectrum are depicted by the red dotted lines in Fig. 7, which agree well with those from SFA. This indicates that this improved two-center model is also adaptive to the case of the anti-bonding linear molecules.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Wave functions of (a) ψO2, (b) ψ1O, and (c) ψ2O.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The variation of harmonic emission spectra from the HOMO orbital of O2 molecule as a function of θ. The red dotted line is the interference minimum obtained by using the improved two-center model.

We investigated the interference minima in the HHG spectra from linear molecules. It is found that the position of the interference minimum is related not only to the nuclear distance between the two main atoms contributing to HHG, but also to the symmetry of the molecular orbital. Hence, the two-center model is reasonably modified by considering the initial phase difference between the double wave sources. The phase differences for the σ and π orbitals can be set as π and zero, respectively. For the anti-bonding orbital, the initial phase difference should be added π compared to that of the bonding orbital. After amending the initial phase difference, the interference minima predicted by the two-center model are in agreement with the results from SFA. Therefore, the modified two-center model can be applied to examine the linear molecular HHG in experiments.