† Corresponding author. E-mail:
An extensive theoretical set of atomic data for Rb XXIX in a wide range with L-shell electron excitations to the M-shell has been reported. We have computed energy levels for the lowest 113 fine structure levels of Rb XXIX. The fully relativistic multiconfigurational Dirac–Fock method (MCDF) within the framework of Dirac–Coulomb Hamiltonian taking quantum electrodynamics (QED) and Breit corrections into account has been adopted for calculations. Radiative data are reported for electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions from the ground level, although calculations have been performed for a much larger number of levels. To assess the accuracy of results, we performed analogous calculations using flexible atomic code (FAC). Comparisons are made with existing available results and a good agreement has been achieved. Most of the wavelengths calculated lie in the soft x-ray (SXR) region. Lifetimes for all 113 levels have also been provided for the first time. Additionally, we have provided the spectra for allowed transitions from n = 2 to n = 3 within the x-ray region and also compared our SXR photon wavelengths with experimentally recognized wavelengths. We hope that our results will be beneficial in fusion plasma research and astrophysical applications.
As lines from fluorine-like ions have been observed in planetary nebulas,[1] solar flares[2,3] and in the spectra of laboratory plasmas,[4,5] atomic data are needed for diagnostic purposes. The factor which makes F-like configuration absolute for detailed study is the nearly full 2p shell which shows that the spectra are not too complex. The 2s22p5–2s2p6 transitions of F-like ions are observed in high-temperature plasmas and can thus be used for plasma diagnostic purposes. Magnetic dipole transitions between fine structure levels separated by spin–orbit interaction such as 2s22p5 2P3/2–2P1/2 transition in fluorine-like ions have important applications in astrophysics[6] and high-temperature plasma diagnostics.[7,8] The transition 2s22p5 2P3/2–2P1/2 is observed in tokamaks and is useful for measuring ion temperatures via Doppler broadening.[9] The emission line ratios involving the 2s22p5 2P3/2, 2s22p5 2P1/2, 2s2p6 2S levels of fluorine-like ions are useful for plasma diagnostics.[10] Forbidden lines of the fluorine isoelectronic sequence with 
The spectroscopy of highly charged ions is of considerable interest in both pure atomic physics and applications such as hot-plasma diagnostics, high temperature astrophysical plasma,[11–13] x-ray laser development and for the study of high-field relativistic and quantum electrodynamic (QED) effects. Transitions in such ions are used to find temperature and density distributions and in calculating stellar envelope opacities.[14] Accurate measurements of energy levels provide tests of modern atomic-structure theory. Accurate atomic data such as transition probabilities, oscillator strengths, and lifetimes of excited levels are requisite in astrophysics, laser spectroscopy, laboratory plasma diagnostic, tokamak devices, and controlled thermonuclear reactions. Accurate atomic data are also needed for reliable interpretation of observed data.[15]
Astrophysical interest in the spectra of multiply charged ions has increased as the maximum number of lines emitted from high Z ions lie within extreme ultraviolet (EUV) 100–1200 Å and soft x-ray (SXR) 1–50 Å regions useful in providing detailed knowledge of coronal atmosphere. Recently, much progress has been made in the study of soft x-ray lasers. The interest in soft x-ray lasers motivates the study of the spectroscopy of highly charged ions.
F-like ions have been studied previously by various authors. Sampson et al.[16] calculated transition probabilities between levels of the 2s22p5, 2s2p6, 2s22p43l, and 2s2p53l configurations using the relativistic distorted wave method. Three lowest energy levels were calculated by Ivanova and Gulov[17] using the relativistic perturbation theory with a model potential. Kim and Huang[18] provided spin–orbit intervals in the ground state 2p5 2P3/2–2P1/2 of F-like ions for Z ≤ 56. Atomic binding energies for lithium to dubnium isoelectronic series in the Dirac–Fock approximation were calculated by Rodrigues et al.[19] Gu M F[20] calculated the level energies of 1s22lq (l ≤ q ≤ 8) states for ions with Z ≤ 60 using a combined configuration interaction and many-body perturbation theory approach. Cheng et al.[21] calculated energy levels, oscillator strengths, and transition probabilities for the first row atoms (Li through F) using the multiconfigurational Dirac–Fock method. Transition energies for ions from Z = 11 to Z = 33 were calculated by Edlén[22] using a semiempirical formula with three adjustable parameters. Some authors[23,24] using the CIV3 code obtained oscillator strengths of transition from the ground state of fluorine-like ions. Nahar[25] obtained atomic data for fluorine-like iron using relativistic Breit–Pauli approximation under the iron project. Fischer and Tachiev[26] obtained energy levels and transition rates for low lying states for ions up to Ti XIV using multiconfigurational Breit–Pauli wavefunctions. Jonauskas et al.[27] calculated energy levels and transition probabilities among levels of the ground and first 23 excited configurations of Fe XVIII using multiconfigurational Dirac–Fock method. Energies and E1, M1, E2 transition rates for 2s22p5 and 2s2p6 configurations states in F-like ions between Si VI and W LXVI were calculated by Jönsson et al.[28]
Feldman et al.[29] identified transitions of the type 2s–2p in the highly charged fluorine-like Mo, Cd, In, and Sn. Transitions of the type 2s–2p were also identified in F-like As, Se, Br, and Rb by Feldman et al.[30] Zigler et al.[31] presented wavelengths and identified 11 x-ray lines due to 2p–3d and 2p–3s transitions in Rb XXIX. The L-shell soft x-ray emission spectra of Cu, Zn, Ga, As, Br, Rb, and Sr from laser-produced plasma sources for 2p5–2p43s, 3d fluorine-like transitions were recorded by Hutcheon et al.[32] Denis-Petit et al. identified x-ray spectra in the Na-like to O-like Rubidium ions in the range 3.8–7.3 Å.[33]
The main focus of our work is to perform fully relativistic calculations in order to obtain transition energies, oscillator strengths, transition rates, and lifetimes for lowest 113 levels of the 2s22p5, 2s2p6, 2s22p43l, 2s2p53l, 2p63l, 2s22p44l, 2s2p54l, 2s22p45l, and 2s2p55l (l = 0,1,2,3) configurations of F-like Rb. In the present calculations, we have adopted the relativistic multiconfiguration Dirac–Fock (MCDF) approach. Such calculations including physical effects of the relativistic two-body Breit interaction and the QED corrections provide accurate tools to test the many-body atomic theory and for plasma diagnostics in high temperature plasmas. We have also provided a comparison of our results with the data compiled by NIST.[34,35] We theoretically identified EUV and soft x-ray transitions and plotted the Rb XXIX spectra. This work is an extension of our previous work[36] in which we investigated the spectra of Sr XXX.
To perform large-scale calculations, the fully relativistic MCDF method originally developed by Grant et al.[37] and revised by Norrington[38] has been adopted which has successfully been applied earlier by ourselves and others.[39–44] It takes into account all the relativistic effects as well as Breit and QED corrections important for highly ionized atoms.
In the MCDF method, the dominant interactions in an N-electron ion or atom are included in the Dirac–Coulomb Hamiltonian
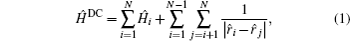

The relativistic atomic state function of an atom or ion is described by an atomic state function (ASF) constructed approximately by a linear combination of configuration state functions (CSFs) with the same parity P and same angular momentum (J, M)

The configuration state functions ϕ, are built as linear combinations of Slater determinants which, in the Dirac–Fock model, is a product of one-electron Dirac orbitals

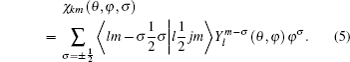

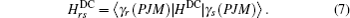

CSFs are obtained from the antisymmetrized products of a common set of orthonormal orbitals which are optimized on the basis of Dirac–Coulomb Hamiltonian. By solving the MCDF equations, the radial functions are determined which depend upon varying the orbital radial functions to obtain an extremum of the energy functional. The wavefunction is expanded to thousands of CSFs and thus enables us to obtain a suitable description of level structure and transition properties for multiple and highly charged ions. Relativistic configuration interaction calculations are then carried out to evaluate CSF expansion coefficients by diagonalizing the Hamiltonian matrix. After obtaining self consistency, the contributions from the Breit interaction, vacuum polarization, self-energy and finite nuclear mass corrections are added as a first-order perturbation correction.
To calculate the radial wavefunctions, we have adopted the extended average-level (EAL) mode for self-consistent calculations in which a weighted trace of the Hamiltonian matrix is minimized. It can assign a configuration of a given weight automatically.
To assess the accuracy of our results from MCDF, we employ another fully relativistic code, the flexible atomic code (FAC)[45] based on Dirac equation. The atomic structure calculations are based on the relativistic configuration-interaction (CI) method. In FAC, the basis state functions are built by radial spinors obtained from a modified Dirac–Fock–Slater central field potential. The orbitals are optimized self-consistently where the average energy of a fictitious mean configuration with fractional orbital occupation numbers is minimized. This mean configuration stands for the average electron cloud of the configurations maintained in the configuration–interaction (CI) expansion. Using the Dirac–Coulomb Hamiltonian, relativistic effects are fully considered. Generally, there is no major discrepancy in the determination of energy levels and radiative data from FAC and MCDF. MCDF provides more options in terms of optimization schemes. The results from FAC will be helpful in assessing the accuracy of energy levels, radiative rates, and oscillator strengths.
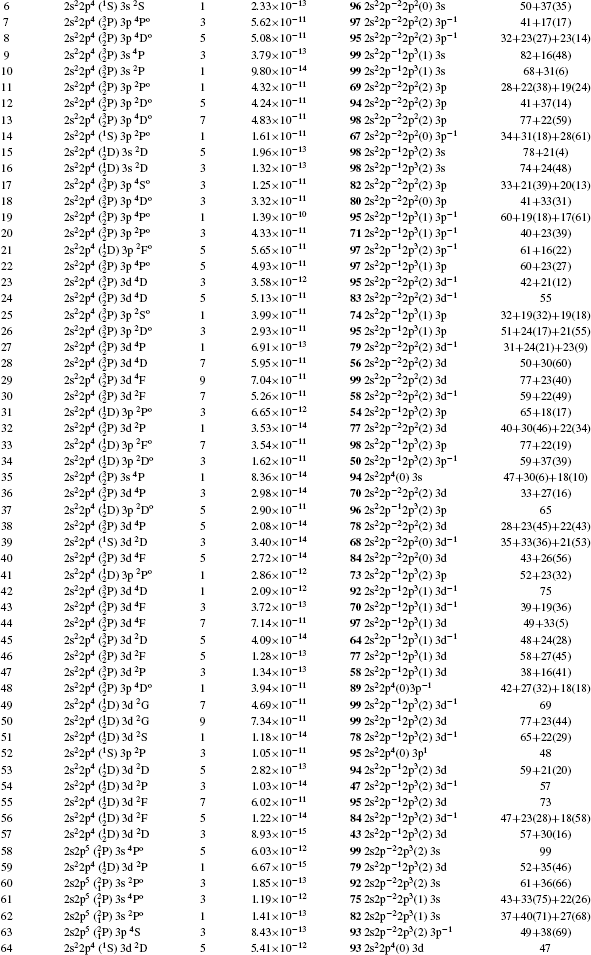
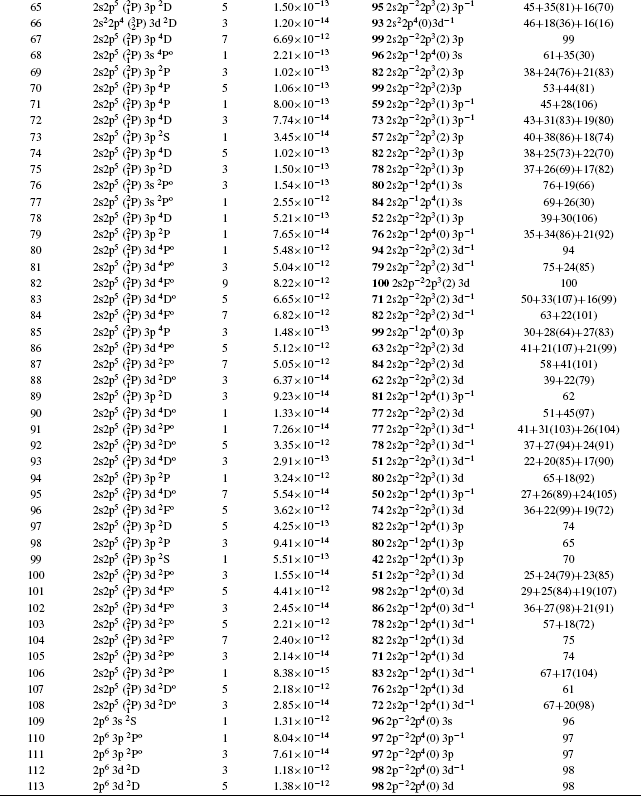
As velocity of electrons in the highly ionized atoms is fast and the nuclear potential energy is very strong, the relativistic effects must be taken into account. Therefore, in this work, calculations have been performed using fully relativistic MCDF approach. As an elaborate CI is needed to achieve a better accuracy, therefore we have included CI among 2s22p5, 2s2p6, 2s22p43l, 2s2p53l, 2p63l, 2s22p44l, 2s2p54l, 2s22p45l, and 2s2p55l configurations, where (l = s,p,d,f). We included correlation effects in the excitation up to the 5f orbital. In the last column of Table 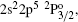
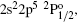



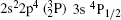
| Table 1. Level No., wave-function compositions and lifetimes of first 113 fine structure levels of Rb XXIX using MCDF. . |
In Table 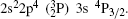
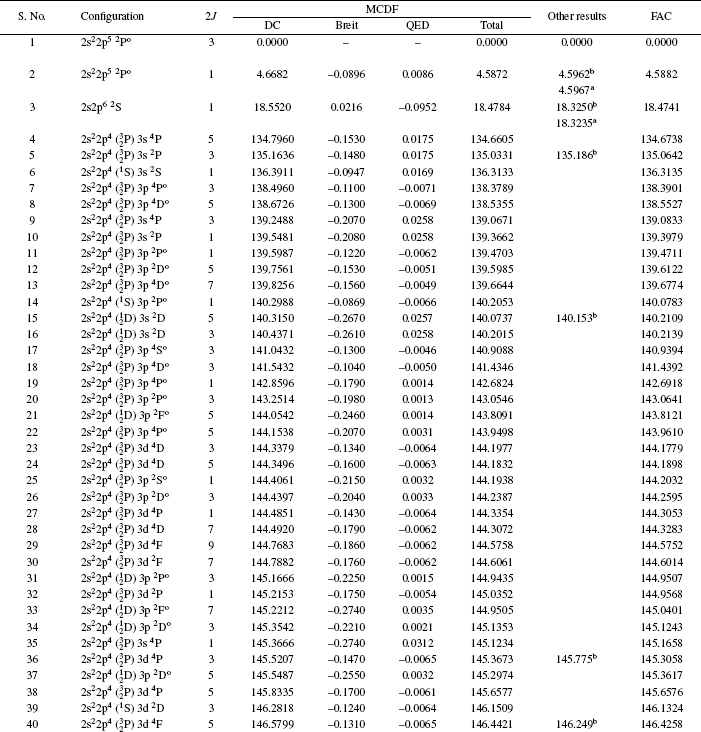
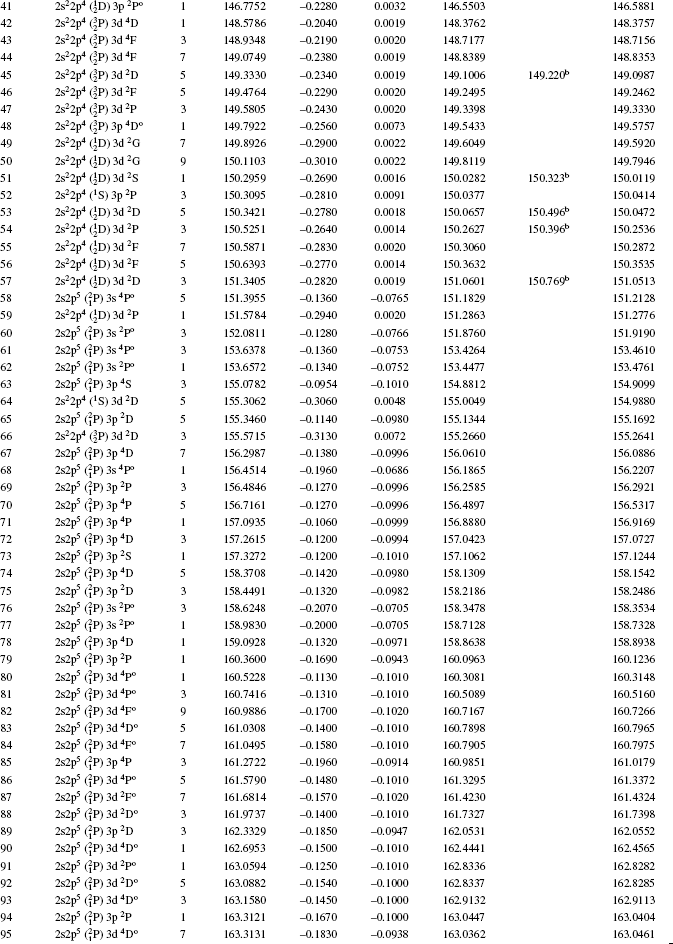
| Table 2. Dirac–Coulomb (DC), Breit and quantum electrodynamics (QED) contributions to the MCDF energy (in Ryd) for the lowest 113 levels for Rb XXIX. The sum total is compared with FAC and other available results. All energies are relative to the ground state. . |
A good agreement between the present calculations and the published data has been found. Taking NIST as a standard reference for comparison, we find that the maximum deviation between the present calculations and NIST energies and present results and Jönsson et al.[28] results is 0.84% for the level 2s2p6 2S1/2. The maximum disagreement of FAC calculations with our MCDF results is within 0.10%.
For a transition i → j, the relation between the absorption oscillator strength fi j (dimensionless), and radiative rate Aji (in s−1) is expressed as

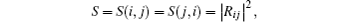
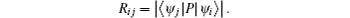
| Table 3. Transition data for E1, E2, M1, M2 transitions for Rb XXIX from |
As the ratio of velocity/length is an indicator of accuracy of f- or A-values, we have also provided the ratios between length and velocity forms. A good agreement between the two forms is always desirable, but not a necessary condition for accuracy. The vel./len ratio in our case is generally within 10% of unity for most of the strong transitions (f ≥ 0.1). For some strong transitions such as 
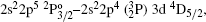
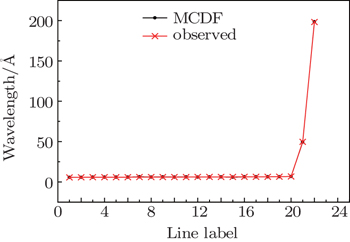
In Table
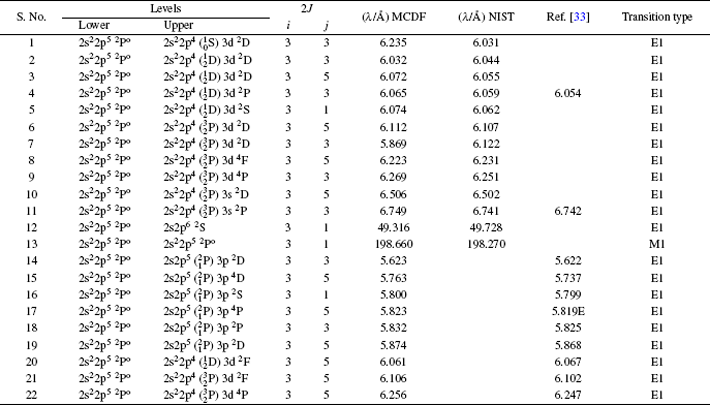
| Table 4. Comparison of computed wavelengths (in Å) with observed wavelengths from NIST and other available results for transitions from |
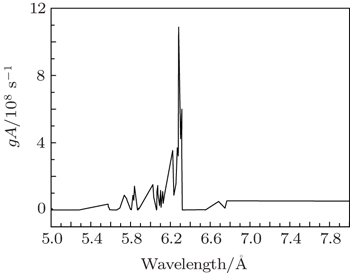
In the present paper, we have presented our calculated wavelengths of EUV and soft x-ray transitions in Table 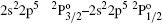
In Table
In Fig.
The lifetime (τ) for a level j for a transition i → j is defined as follows:

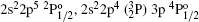
In this paper, we have reported energy levels for the lowest 113 levels and radiative rates for E1, E2, M1, and M2 transitions from the ground level of Rb XXIX. Two independent calculations have been carried out using the MCDF and FAC codes. A comparison between the two sets of energy levels, as well as with the other available results, shows a satisfactory agreement. Wavefunction composition has been provided in both LSJ and JJ couplings. Though every care has been taken to identify the levels based on the strength of their eigenvectors, a possibility of their re-designation still remains. EUV and SXR transition wavelengths have been calculated using MCDF method. Comparisons have also been provided, for transition wavelengths for some selected transitions with NIST and other observed values are found to be in good agreement. The vel/len ratio is within 10% of unity, in particular the strong transitions with f ≥ 0.1 confirms the accuracy of our results.
Finally, the lifetimes for all 113 levels have been reported, although, due to paucity of data no comparisons with measured values are possible. However, our calculations will be helpful for an accuracy assessment for future measurement of lifetimes.
We have obtained new and previously unpublished energy levels, oscillator strengths, and transition probabilities for Rb XXIX. Hopefully, the present wide range of data will be useful in astrophysics, modeling of a variety of plasmas and for line identification in future experimental work.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 |