As the first of the rare-earth elements with f electrons, cerium is unique and continues to generate both theoretical and experimental works.^[1–9] Among its intriguing physical and chemical properties, the most fascinating is the first-order isostructural phase transition. This involves a magnetic, high-temperature low-density γ phase and a nonmagnetic, low-temperature high-density α phase. At room temperature and a pressure of about 0.7 GPa, the γ-Ce collapses into α-Ce with a volume decrease of about 15%–17%, leaving the crystal structure unchanged as face-centered cubic (fcc).^[10–13] Although it is a common consensus that the isostructural transition is tightly linked to the behavior of the 4f electron, the nature of the transition is still unclear.^[14–26] The transition was first explained by the promotion of a f electron into spd orbital under pressure,^[14] but it was refuted by experiments.^[15,17] Nowadays two main theoretical pictures remain under debate: the Mott transition^[12] and the Kondo volume collapse (KVC).^[18] According to the Mott model, the transition is owing to the electron hopping between f orbitals, which changes drastically across the transition between the γ phase and α phase. In the KVC model, the transition is induced by the rapid change of the coherence temperature across the transition boundary, which affects dramatically the structure of the conduction spd electrons through the Kondo effect. Both models agree with many aspects in experiments, including photoemission and spectroscopy, as well as x-ray and neutron diffraction.^[22–26] However, a recent theoretical study^[8] argued that neither the KVC model nor the Mott model is sufficient to describe the isostructural transition.

The pressure–temperature (PT) phase diagram regarding to the transition between γ and α phases is extremely interesting because it is the only solid–solid transition in all elemental metals which has a phase boundary terminating at a critical point (CP), analogous to the well-known liquid–gas critical point. There are several puzzling questions about the γ- and α-Ce phase diagram, including the position of the CP (1.5 GPa, 480 K;^[22] 1.75 GPa, 550 K;^[27] 2 GPa, 600 K;^[11] 2.05 GPa, 640 K^[28]), and the possibility that the phase change continues as a second-order transition towards the melting line such that the critical point is in fact a tri-critical point.^{[22,24,29,30]} Moreover, the fundamental interpretation and understanding of the CP remains unclear, and it seems difficult to theoretically reproduce the linear dependence between the transition temperature and pressure,^[20,31] which was observed in experiments.^[11] In order to have insight into these problems, we try to construct precise equations of state (EOS) for γ- and α-cerium based on first-principles calculation. Versus previous literatures,^{[20,21,31,32]} our work pays more attention to the strong anharmonic effects of the ions that have been generally observed in rare elements. The variation in the magnetic moment of the γ-Ce atom has also been considered. Our calculations bring forward a different interpretation of the well-known CP, and predict that another part of phase boundary in pressure–temperature space may exist except for the commonly known boundary.

The equation of state is obtained by calculating the Helmholtz free energy, which is written as

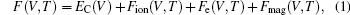
Ab inito calculations were carried out by DFT+U method with the spin-dependent GGA and PAW-PBE pseudopotential implemented in VASP package.^[33] During all ab initio calculations, the 5s²5p⁶4f¹5d¹6s² were treated as valence electrons, and a 16× 16× 16 Γ-centered k mesh, 650-eV plane-wave kinetic cutoff was used. The self-consistence convergence energy was set to 10⁻⁷ eV to ensure high precision.

The appropriate values of U for Ce 4f electron have been debated in the literature.^{[31,32,34–36]} Here, for every cell volume and electronic temperature, 7 values (1.0, 1.6, 2.0, 3.0, 4.0, 5.0, and 6.0 eV) are selected to carry out the calculations. Thereafter, the free energy is fitted to a parameterized function F(V,T,U) (U is treated as a parameter), and the most suitable values of parameter U for both γ- and α-Ce are finally determined by general comparison of the thermodynamic properties and phase diagram between theory and experiment.

We complete 9 different electronic temperatures from 100 K to 900 K with 100 K interval and 24 different volumes from 22.78125 Å³/atom to 41.59375 Å³/atom. The calculated cold energy and thermal electronic free energy are fitted to Vinet’s universal formula^[37] and second-order homogeneous polynomial, respectively,

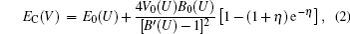
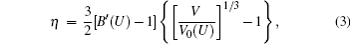
The ion vibration of rare-earth elements exhibits strong anharmonic effects. Thus, we use a quasi-harmonic model to predict the vibrational free energy

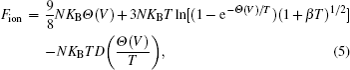
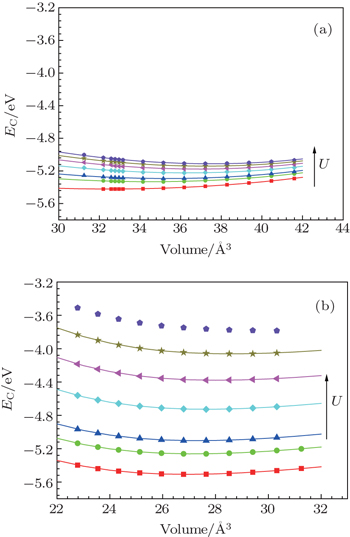
Until recently, no accurate expression exists for the magnetic free energy F_mag. Allen,^[20] Johansson,^[21] Laegsgaard,^[31] and Wang^[32] used the magnetic entropy to describe one atom of γ-Ce as S_mag = K_B ln[2J + 1.0] (J = 5/2) for the total angular moment of the 4f electron. This estimation is based on the assumption that the 4f orbits are filled with one electron all the time, but our ab initio calculations reveal the occupation of 4f and the total magnetic moment changes with the cell volume and electronic temperature. To take this change into consideration, we write the specific magnetic free energy of γ-Ce as

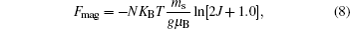
Figure 1 shows the cold energy curves of γ- and α-Ce collected from ab initio calculations with different U values. The cold energy of both phases increases with increasing values of U. When U > 5.0 eV, the increase in cold energy of γ-Ce becomes very small. The value of U for α-Ce could not be greater than about 2.0 eV, otherwise γ-Ce becomes the stable phase in theory near zero pressure and temperature, which is in contrast to the experimental data.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Cold energy calculated for U = 1.0, 1.6, 2.0, 3.0, 4.0, 5.0, 6.0 eV. (a) γ-Ce and (b) α-Ce. Scatter symbols are calculated data from ab-initio. Solid lines are fitted.

By comparing theory and experiment on mass density, isotherms, phase diagram, as well as other thermodynamic data, the most appropriate values of U are 2.0 eV for γ-Ce and 1.5 eV for α-Ce, which are very close to Ref. [35] (1.5 eV) and Ref. [32] (1.6 eV). In Ref. [19], Liu et al. found that when fitting to Bremsstrahlung isochromatic spectroscopy data, the value of U should be 5.44 eV for γ-Ce and 5.34 eV for α-Ce, whereas 6.0 eV is most suitable for both γ- and α-Ce via 3d x-ray photoemission spectroscopy and the 4f photoemission. Accordingly, Laegsgaard and Svane^[31] and Amadon et al.^[34] used 6.0 eV in their ab initio calculations for γ- and α-cerium. The values determined here are much smaller than Liu et al. In fact, the parameter U is simply an empirical effective parameter introduced by the simplified Anderson single impurity model to describe the electron–electron on-site strong interactions. How to best determine its value remains a matter of debate. One well-accepted way is to examine the theoretical prediction and experimental measurement on a certain specific property. Thus, it is not inappropriate that the electronic property and thermodynamic property of cerium require different values of U due to different sensitivities. We note in Refs. [31] and [34] that the authors did not check the phase stability at zero pressure and temperature and used 6.0 eV as the value of parameter U for both γ- and α-Ce.

Figure 2 shows the calculated total magnetization of an atom of γ-Ce. At lower temperatures, the total magnetization first increases with increasing cell volume and reaches a maximum value, and then decreases with further increasing cell volume. At high temperatures, the total magnetization increases monotonously with increasing cell volume and reaches a maximum. In the meantime, the top value of the total magnetization curve decreases with increasing temperature. It is vital for the EOS to take into account the variation of magnetization. Previous works did not do this, which may affect their EOS.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Variation in the total magnetization moment of atom with U = 2.0 eV. Scatter symbols are calculated data from ab-initio. Solid lines are fitted results.

There are a few model parameters in our EOS calculations, β in Eq. (5), Θ (V₀) in Eq. (7), and g in Eq. (8). Rosen^[42] measured the Debye temperature of α-Ce at 4.2 K to be 154.0 K. This is the most similar experimental value we find at zero temperature and ambient pressure. Hence, for Θ (V₀) of α-Ce, we use 154.0 K. As for γ-Ce, we use a recently measured value of 132.8 K by Decremps.^[13] We currently have no special method to estimate β and g, and thus their values have to be determined by requiring global agreement on thermodynamic properties and phase diagrams between theory and experiments. All EOS parameters for both γ- and α-Ce are listed in Table 1.

Table 1.

Table 1.

Table 1. Parameter values obtained or used in this EOS calculation. . Parameter This work Experiments γ-Ce α-Ce γ-Ce α-Ce 34.48[46] 29.0[46] V0/Å3 35.33 27.09 34.36[47] 28.17[47] 34.4[11] 28.5[11] E0/eV −5.2927 −5.3017 B0/GPa 22.93 40.98 21.0[46] 27.0[48] 23.9[48] 35.0[45] B′ −2.55 5.15 U/eV 2.0 1.5 β/K−1 −1.3 × 10−4 −9.0 × 10−4 Θ (V0)/K 132.8 154.0 g 1.25 /

Table 1. Parameter values obtained or used in this EOS calculation. .

The pressure derivative of bulk modulus (B′) of γ-Ce is negative, which is consistent with the experimental measurements carried out by Jeong^[12] and Decremps.^[13] The V₀ is larger than the experimental value at ambient conditions. It is reasonable to consider that the thermal expansion of γ-Ce is abnormal. The value of V₀ for α-Ce is obviously smaller than the experimental measurements, which is a direct result of the smaller value for U (1.5 eV) in the DFT+U ab initio calculations. Increasing U to greater than 4.0 eV may increase V₀ to the experimental value, but it increases the energy of α-Ce above that of γ-Ce. This conflicts with the experimental study which indicated that α-Ce is the stable phase at the vicinity of zero temperature and pressure.

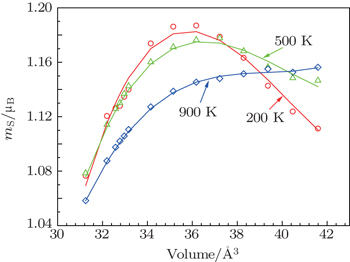
Our calculated bulk modulus B of α-Ce is higher than the experimental measurement, but consistent with other first-principles calculations.^[21,43,44] The discrepancy between theory and experiments reflects the limitation of DFT+U calculation. Figure 3 shows the theoretical isotherms of γ- and α-Ce at room temperature, which are in good agreement with experimental results. The calculated heat capacity C_v under ambient conditions is 190.43 J/kg·K. This agrees well with the experimental value 192.26 J/kg·K.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Calculated isotherm at room temperature. (a) γ-Ce, (b) α-Ce.

As a common knowledge, the phase boundary in P–T space can be achieved by calculating G_γ (P,T) = G_α (P,T) (Gibbs free energy). Our calculation predicts that the γ- and α-Ce phase boundary is composed of two segments, illustrated in Fig. 4 as segment I and segment III. Segment I is in good agreement with experiments, but segment III has never been reported before. In the meantime, it is very interesting to find that the segment connecting the end points of segments I and III (labeled as segment II in Fig. 4) is essentially a critical boundary for γ-Ce, which means that at its right side (in the higher temperature and pressure region) compressing γ-Ce will lead to decrease of pressure, therefore γ-Ce is unstable. The new picture of the phase diagram simultaneously clarifies the significance of the well-known critical point (CP point in Fig. 4), which has already puzzled scientists for decades.

Fig. 4.

Figure Option ViewDownloadNew Window

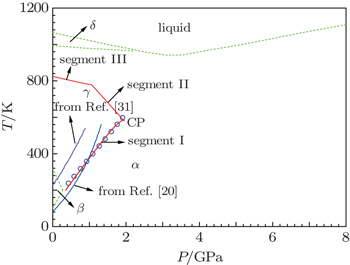Fig. 4. Phase diagram. Experimental data regard to the phase boundary between γ and α phases (open circle). The green dashed lines are from Ref. [11]. The blue and violet solid lines are the theoretical phase boundary for γ and α phases from Refs. [20] and [31], respectively. The segment I, II, and III are the theoretical lines of present work. Across segment I and III represents an event of first-order phase transition. Across segment II implies that γ-Ce becomes unstable.

In a recent work,^[22] Lipp et al. reported that the data of minimum in bulk modulus seems to imply that the commonly known phase boundary (segment I in this work) would continue toward the nearby region with minimum melting. This contradicts our prediction. However, it remains unclear what would be across the critical boundary (segment II). An intermediate meta-stable phase or some kind of pseudo-alloy^[21,22,32] might explain their experiments.

In addition, at room temperature (298 K), our EOS predicts that the γ → α transition occurs at 0.71 GPa accompanied by a 17.7% volume collapse and a 1.56 K_B/atom entropy change. This is in good agreement with experimental values of 0.7 GPa, 17%, and 1.54 K_B/atom.^[11–13,20]

In conclusion, high-precision two-phase equations of state for γ- and α-Ce were constructed to clarify puzzling problems and controversies about their phase diagram. Versus previous works, more attention was paid to the strong anharmonic effects of the ions that have been generally observed in rare elements. The variation in the magnetic moment of the γ-Ce atom has also been considered. The new EOS generally agrees well with experimental data regarding thermodynamics, phase diagrams, and phase transitions.

Moreover, the new EOS indicates that another segment of phase boundary for γ- and α-Ce (segment III in Fig. 4) may exist except for the well-known part of boundary. Also the new EOS simultaneously predicts that γ-Ce has another critical boundary (segment II in Fig. 4) beyond which the γ phase is unstable, and the commonly well-known critical point is actually one of its two end points.