Cite this Article
Li Song, Chen Shan-Jun, Chen Yan, Chen Peng. Ab initio investigation of sulfur monofluoride and its singly charged cation and anion in their ground electronic state. Chinese Physics B, 2016, 25(3): 033101  
Permissions
Ab initio investigation of sulfur monofluoride and its singly charged cation and anion in their ground electronic state
Li Song†, , Chen Shan-Jun, Chen Yan, Chen Peng
School of Physics and Optoelectronic Engineering, Yangtze University, Jingzhou 434023, China

 

† Corresponding author. E-mail: lsong@yangtzeu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11304023 and 11447172), the Young and Middle-Aged Talent of Education Burea of Hubei Province, China (Grant No. Q20151307), and the Yangtze Youth Talents Fund of Yangtze University, China (Grant No. 2015cqr21).

Abstract
Abstract

The SF radical and its singly charged cation and anion, SF+ and SF−, have been investigated on the MRCI/aug-cc-pVXZ (X = Q, 5, 6) levels of theory with Davidson correction. Both the core–valence correlation and the relativistic effect are considered. The extrapolating to the complete basis set (CBS) limit is adopted to remove the basis set truncation error. Geometrical parameters, potential energy curves (PECs), vibrational energy levels, spectroscopic constants, ionization potentials, and electron affinities of the ground electronic state for all these species are obtained. The information with respect to molecular characteristics of the SFn (n = −1, 0, +1) systems derived in this work will help to extend our knowledge and to guide further experimental or theoretical researches.

PACS: 31.15.A–;31.15.vn;33.15.Mt;
Keyword:equilibrium geometrical parameters;potential energy curves;spectroscopic constants;vibrational energy levels;
1. Introduction

Sulfur monofluoride radical is an important species in the fields of atmospheric chemistry and semiconductor industry. The radical is one of the major products of chemical decomposition of SF6, and it takes part in the quenching process in high-voltage power systems.[1] The interest in the SF radical is also attributed to its generation in the plasma discharges employed for etching processes.[2] To better understand the role the radical plays, detailed information with respect to its fundamental properties is required.

The first experimental investigation of SF radical was performed by Carrington et al. with the gas-phase electron paramagnetic resonance technique in 1969.[3] Analyses of the observed spectra yielded equilibrium bond length and effective rotational constant in the ground 2Π3/2 state. The 2Π–2Π transitions were detected by Lonardo and Trombetti in the wavelength region of 4000–3300 Å.[4] Quantitative analyses according to the spectra derived comparable rotational constant with that reported by Carrington et al.[3] Spectrum attributed to SF was also recorded by Hildenbrand with the mass spectroscopy.[5] Based on their analyses, the dissociation energy D0 was obtained. Value of D0 was also determined by Kiang and Zare from the time-of-flight chemiluminescence detection.[6] Improved molecular constants were derived with the microwave spectrometer[7–9] as well as the infrared diode laser spectrometer.[10] The modified RKR method was used by Reddy et al.[11] to determine the vibrational energy levels and dissociation energy of the SF molecule. Theoretically, the methodologies of the HF,[12] CNDO/2,[13] CI,[14] CEPA,[14] DFT,[15–17] G2,[18–20] G3,[20] CCSD(T),[21–24] MRCI,[24–28] and R-matrix[29] were performed for this radical on its geometrical, thermodynamic, and electron collision properties. In these studies, computation results of the equilibrium bond length derived from the CCSD(T) and the MRCI methods with the basis set superior than aug-cc-pVQZ, 1.5983 Å,[24] 1.605 Å,[26] 1.5991 Å,[27] and 1.6040 Å,[28] were closer to experimental results than other approaches, such as MP2, DFT, and CEPA.

In contrast to extensive research on SF radical, much less effort has been made for its singly charged ions, SF+ and SF−. With the aid of the mass spectrometry, Hildenbrand[5] and Fisher et al.[30] provided us the experimental determination of D0 for SF and SF+ with values of 3.51(5) eV and 3.56(5) eV, respectively. To our knowledge, the only experimental datum of SF− for which one can compare was reported by Polak et al.[31] According to the spectrum recorded by a photoelectron spectrometer, Re and ωe of the anion were determined to be 1.717(15) Å and 635(15) cm−1. For both molecular ions, several theoretical investigations were also carried out with HF,[12] MP4,[32] G2,[18–20] G3,[20] DFT,[15–17,33] CCSD(T),[17,21,23] and MRCI[24] methodologies. Among these computations, geometrical parameters obtained on the CCSD(T)/AVQZ,[21] CCSD(T)/cc-pVQZ,[23] and MRCI+Q/AV5Z[24] levels are believed to be trustable than other predictions owing to the high-level methods and relative large basis sets.

In the present work, we have performed high-level computations on the SFn (n = −1, 0, +1) systems to derive their geometrical parameters, spectroscopic constants, PECs, and vibrational energy levels for the ground electronic states. Our aim is to provide accurate information, which are prerequisites for us to understand specific bonding natures, chemical activity, characteristics of photochemistry and thermochemistry, as well as spectroscopic features and reaction dynamics, for systems of interest.

2. Computational details

The multi-reference characters of the neutral and ionic SF systems are assessed by utilizing the method of the T1 diagnostics, and the features are found to be quite significant according to our evaluations. Therefore, our computations for these systems are performed at the multi-reference configuration interaction (MRCI) level,[34] based on the complete active space SCF (CASSCF) wavefunctions,[35] with Davidson correction. In order to take into account the electron correlation effect sufficiently, except electrons of F 1s and S 1s are not optimized, all other electrons, including F 2s22p5 and S 2s22p63s23p4, are used in our correlation energy calculations. All energy calculations in this work have been performed with the MOLPRO package.[36] The augmented correlation-consistent basis sets aug-cc-pVXZ (X = Q, 5, 6) of Dunning and co-workers are utilized. The largest basis sets AV6Z are (17s, 11p, 6d, 5f, 4g, 3h, 2i) primitive Gaussian functions contracted to [8s, 7p, 6d, 5f, 4g, 3h, 2i] for F atom, and (22s, 15p, 6d, 5f, 4g, 3h, 2i) to [9s, 8p, 6d, 5f, 4g, 3h, 2i] for S atom. The core–valence (CV) correlation is carried out with the CV basis set aug-cc-pCV5Z, and the relativistic correction is taken into account with the aug-cc-pV5Z-DK basis set coupled with the third-order Douglas-Kroll hamiltonian (DKH3) approximation.[37,38] It should be pointed out that the two correction calculations are applied across the entire PEC.

The corrected total energies are then extrapolated to the CBS limit with the following functions:[39,40]

and

where X = 4, 5, 6 for AVQZ, AV5Z, and AV6Z, respectively. Our final CBS estimation is the average of the two extrapolation results and is denoted by CBS throughout this paper. This computational scheme has been used to study several neutral and ionic systems by our group,[41–43] and the uncertainties are expected to be less than 0.0002 nm for Re and 0.01 eV for the dissociation energy D0.

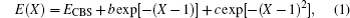
The Murrell–Sorbie (MS) potential energy function[44] is used to represent potential interactions of the present diatomic systems. It is given by

where ρ = R − Re, with R and Re being internuclear distance and equilibrium internuclear distance, respectively, and De is the well depth. In consideration of both accuracy and efficiency, the MS function with n = 15 is used in our fittings in the present paper with all parameters floated.

The LEVEL 8.0 program package[45] is used to determine the vibrational energy levels as well as the rotational and centrifugal distortion constants for each level according to our equilibrium geometrical parameters and PECs by numerically solving the one-dimensional Schrödinger equation of nuclear motion.

3. Results and discussion
3.1. PECs and equilibrium internuclear distances

The PECs of all species are calculated over the internuclear separation range from 0.09 nm to 1.0 nm at intervals of 0.005 nm, which declines to 0.002 nm in the vicinity of the energy minima on each PEC. By fitting energy points to the 15-parameter MS function, PECs of the three systems are obtained and illustrated in Fig. 1. We can conclude that if the SF radical captures an additional electron and becomes SF−, the equilibrium bond length increases while the absolute total energy at Re decreases. On the contrary, Re shortens slightly and E (at Re) increases significantly when the radical loses an electron. The equilibrium geometrical parameters of the systems are tabulated in Table 1, including the equilibrium internuclear distance Re, the total energy E at Re, and the dissociation energy D0. Also presented in the table are available literature results.

Fig. 1. PECs of the ground states of SF, SF+ and SF−.
Table 1.

Equilibrium geometrical parameters of SF (X2Π), SF+(X3Σ−) and SF−(X1Σ+).

.

Our final estimation of Re for SF radical, 0.15935 nm, deviates just ∼ 0.17% from the experimental result of 0.1596244(22) nm.[10] Comparing our result with previous theoretical predictions, it is found that our datum agrees with those values quite well, especially with recent CCSD(T)[21–24] and MRCI[24–28] computations. As all other theoretical studies have been done either within small- to moderate-size basis sets or without sufficient consideration of electron correlation effect, our high-level computations are anticipated to yield more trustable predictions.

As for the ionic SF systems, our estimates for Re of SF+ and SF− is 0.14965 nm and 0.17119 nm, respectively. Although several spectroscopic detections were performed, only one study[31] presented experimental determination of Re for SF− and no report of Re was found for SF+ to the best of our knowledge. For SF−, our Re agrees with that reported by Polak et al.,[31] 0.1717(15) nm, quite reasonable. The lack of data made it impossible for us to perform detailed comparisons and further discussion. Nevertheless, from another point of view, this also makes our theoretical result a useful source of information for geometrical parameters of both SF+ and SF−, which should be of interest to experimentalists.

3.2. Absolute energies at Re and dissociation energies

The total energies at the equilibrium internuclear distance of each species are summarized in Table 1, which is −499.03336 Eh, −498.60795 Eh, and −497.83289Eh for SF, SF+, and SF−, respectively. As our investigation includes the process of extrapolating to the CBS limit with basis sets up to sextuple-zeta quality and the contributions of corrections from CV correlation and relativistic effect, our data are expected to be more reliable than previous theoretical estimates.

For further confirmation of the dissociation channel of the ground electronic states of the present systems, we have performed MRCI computations on the ground and several low-lying excited states of both ionic systems. However, as this work focuses on the ground states, no discussion associates with excited states will be presented here. Based on our computation, the dissociation channels of the ground state for the two ionic species are

and

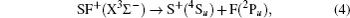
According to our MRCI/CBS calculation, our D0 is 3.627 eV, 3.711 eV, and 3.629 eV for SF, SF+ and SF−, respectively, as listed in Table 1. Our data agree well with experimental values in Refs. [5] and [6] of less than 3% for the neutral SF, and with that in Ref. [30] of no more than 4% for the cation. For both SF and SF+, the values of D0 in this work are consistent with previous theoretical investigations. As for the anion, no experimental determination of D0 was given.

Inspection of Table 1 shows that D0 of SF− reported in Refs. [12], [17], and [31]-[33] deviated away from that derived in this work and in other literatures available. To account for the discrepancy, it can be attributed to the wrong dissociation channels used in those studies. For example, D0 of SF− obtained by Polak et al.,[31] which is 2.40(9) eV, was derived from their thermodynamic calculation according to the experimental values of D0(SF) = 3.52(9) eV [5], EA(F) = 3.4011887(32) eV,[46] and EA(SF) = 2.285(6) eV [31] with the following formula:

which suggests that SF− dissociated as S+F−. Based on our determination of dissociation channel for SF−, which is S−+F, the thermodynamic calculation should use EA(S), 2.077104(3) eV,[47] instead of EA(F) in Eq. (6). As the difference between EAs of sulfur and fluorine, which has been presented above, is calculated to be EA(F)−EA(S) = 1.324 eV, combined with 2.40 eV in Ref. [31], we obtain D0 of 3.724 eV with respect to the correct dissociation channel, and this value agrees with our estimate quite well. Although the CBS result (4.075 eV) derived from the CCSD(T)/cc-pwCVXZ(DTQ) computation in Ref. [23] was close to our value, it should be mentioned that the dissociation channel, which was assumed to have been formed with S(1D) and F−(1S) by Czernek and Živný, was not for the ground electronic state.

For all three species, their D0 values are quantitatively similar. The relative large D0 indicates that the neutral FS and its singly charged ions are almost equally strong bounded, and this character of electronic stability ensures the feasibility of performing experimental detections, especially for ionic species, which is a favorable message for spectroscopists. However, to accurate determine D0 of all these species, it is necessary to consider contributions due to nonadiabatic coupling or atomic fine structure and hyperfine structure from successful experimental investigations.[48–51]

3.3. Spectroscopic constants and vibrational energy levels

Table 2 presents our fitting parameters a1 to a15 of the M–S function. We use the root mean square (RMS) error with the expression of

to evaluate the quality of our fittings. In Eq. (7), N is the number of fitting points, Vfit and Vcal are fitted and calculated energies, respectively. ERMS for the three systems are listed in Table 2, and the results are reasonable. The force constants, independent of atomic masses, are calculated from the fitting parameters as well as the geometrical parameters, and are also collected in Table 2.

Table 2.

Fitting parameters of the MS function and force constants of SF, SF+ and SF− in their ground electronic states.

.

Spectroscopic constants of selected isotopes, 32S19F, 34S19F, 32S19F+, 34S19F+, 32S19F−, and 34S19F−, of the present systems are listed in Table 3. Isotopes containing 33S and 36S are not considered in this work owing to their low natural abundance. Literature results are also included in the table, although the results were derived from the standard atomic weight of each element. Reasonable agreement is observed between our spectroscopic constants and available experimental values in Table 3. The equilibrium rotational constant Be and equilibrium vibrational frequency ωe of the neutral, cation, and anion species is ∼ 0.55 cm−1 and ∼ 840 cm−1, ∼ 0.62 cm−1 and ∼ 1020 cm−1, ∼ 0.48 cm−1, and ∼ 650 cm−1, respectively.

Table 3.

Spectroscopic parameters of SF, SF+ and SF− (in cm−1).

.

The microwave investigation carried out by Morino and Yamada[9] in 2001 provided accurate spectroscopic constants of SF with Be = 0.5529450(2) cm−1 and centrifugal distortion constant Drot = 9.7484(2) × 10−7 cm−1. It is found that our predictions of both Be and Drot are in good accord with these experimental results with slight deviations of ∼ 0.1%. Our constants of ωe, αe, and ωeχe are also in excellent agreement with those obtained by the infrared study.[10] For example, experimental value of ωe was determined to be 837.6418(13) cm−1. The difference between this result and our estimate is just several wavenumbers. To sum up, our computation results of the neutral SF radical can be considered as a trustworthy source of information. Moreover, this provides evidence of the reliability of our data for both SF+ and SF−.

The vibrational energy levels of the ground electronic states for above-mentioned isotopes are obtained by solving the one-dimensional Schrödinger equation of nuclear motion (with the rotational quantum number J = 0) with the LEVEL program. The rotational constants and high-order centrifugal distortion constants are derived. Table 4 lists energy levels G(v), rotational constants Bv, and quadruple centrifugal distortion constants Dv of neutral SF with the vibrational quantum number v up to 20.

Table 4.

Vibrational energy levels, rotational constants and centrifugal distortion constants for SF with J = 0 (in cm−1).

.

According to the infrared data,[10] Reddy et al. constructed the PEC of the ground state of SF by using a modified RKR method[11] and derived the vibrational energy levels, which provide us an opportunity to evaluate the reliability of our results. In Table 4, vibrational energy levels for SF of both our data and literature ones are tabulated. In consideration of the isotopic abundance of 32S far overweigh that of 34S, our data agree with those literature ones, which are obtained based on the standard atomic weight, quite reasonable. Vibrational energy levels and spectroscopic constants for ionic SF are listed in Table 5. Our data can be taken as estimations of the missing experimental values and can support further studies such as isotope identification and spectrum detection.

Table 5.

Vibrational energy levels, rotational constants and centrifugal distortion constants for SF+ and SF− with J = 0 (in cm−1).

.
3.4. Ionization potentials, electron affinities, and vertical detachment energies

By using the MRCI method, coupled with the AV6Z basis set, the adiabatic ionization potential (AIP), vertical ionization potential (VIP), adiabatic electron affinity (AEA) and vertical electron affinity (VEA) of the SF radical, as well as the vertical detachment energy (VDE) of the corresponding negative molecular ion, have been determined. Estimations from this work are shown in Table 6 with the inclusion of several literature data. Our AIP result is 10.01 eV, which agrees excellently with the experimental measurements.[5,30] Besides, the agreement for AEA between this study and Ref. [31] is also reasonable, with a slight deviation of ∼ 7%. Therefore, we are confident about the reliability of our VIP, VEA, and VDE results, which are expected to be trustworthy results, although several literature predictions were consistent with our data. The present VIP, 10.16 eV, provides valuable reference for predicting and detecting the photoelectron spectrum of the SF system because the value of VIP can be used to compare with the measured maximum peak of a photoelectron spectrum directly. Owing to the positive VEA of 1.95 eV, the attachment of an electron to the neutral SF is energetically advantageous. Both positive values of EAs suggest removal of an electron from the anion depends on energy input. In addition, the stability of the anion with respect to vertical electron autodetachment is also evidenced by the positive VDE, which is 2.29 eV derived from this work.

Table 6.

Ionization potentials and electron affinities of SF and vertical detachment energies of SF− (in eV).

.
4. Conclusion

We have aimed at theoretical investigations on the SF radical and its singly charged cation and anion, SF+ and SF−. The geometrical structures, potential energy curves, spectroscopic parameters, vibrational energy levels, ionization potentials and electron affinities of the ground electronic state for the three systems have been studied. Computations are performed on the MRCI/aug-cc-pVXZ (X = Q, 5, 6) levels of theory coupled with the technique of CBS extrapolation and consideration of the core–valence correlation and the relativistic effect across the entire PEC. Excellent agreement on geometrical parameters and spectroscopic constants between previous experimental results and our theoretical ones demonstrates the reliability of our data. The information extracted from this work is anticipated to extend our understanding on characteristics of diatomic SF systems, including singly charged molecular ions, and to guide and assist laboratorial detections of these species, which are difficult to exam owing to their nature of high activity.

Reference
1Coufal O 1998 J. Phys. D: Appl. Phys. 31 2025
2Manos D MFlamm D L1989Plasma Etching: An IntroductionBostonAcademic
3Carrington ACurrie G NMiller T ALevy D H 1969 J. Chem. Phys. 50 2726
4Lonardo G DTrombetti A 1970 Trans. Faraday Soc. 66 2694
5Hildenbrand D L 1973 J. Phys. Chem. 77 897
6Kiang TZare R N 1980 J. Am. Chem. Soc. 102 4024
7Amano THirota E 1973 J. Mol. Spectrosc. 45 417
8Endo YSaito SHirota E 1982 J. Mol. Spectrosc. 92 443
9Morino IYamada K M T 2001 J. Mol. Spectrosc. 207 10
10Endo YNagai KYamada CHirota E 1983 J. Mol. Spectrosc. 97 213
11Reddy R RReddy A S RRao T V R 1986 J. Quant. Spectrosc. Radiat. Transfer 35 167
12O’Hare P A GWahl A C 1970 J. Chem. Phys. 53 2834
13Companion A L 1972 Theoret. Chim. Acta 25 268
14Staemmler V 1982 Theoret. Chim. Acta 62 69
15Ziegler TGutsev G L 1992 J. Chem. Phys. 96 7623
16King R AGalbraith J MSchaefer III H F 1996 J. Phys. Chem. 100 6061
17Bauschlicher C WJr.Ricca A 1998 J. Phys. Chem. A 102 4722
18Irikura K K 1995 J. Chem. Phys. 102 5357
19Cheung Y SChen Y JNg C YChiu S WLi W K 1995 J. Am. Chem. Soc. 117 9725
20Miller T MArnold S TViggiano A A 2003 Int. J. Mass Spectrom. 227 413
21Živný OCzernek J 1999 Chem. Phys. Lett. 308 165
22Nielsen I M BZou S LBowman J MJanssen C L 2002 Chem. Phys. Lett. 352 26
23Czernek JŽivný O 2004 Chem. Phys. 303 137
24Woon D EDunning T HJr. 2009 J. Phys. Chem. A 113 7915
25Yang XBoggs J E 2005 J. Chem. Phys. 122 194307
26Woon D EDunning T HJr. 2009 Mol. Phys. 107 991
27Leiding JWoon D EDunning T HJr. 2012 J. Phys. Chem. A 116 1655
28Zhu Z LLang J HQiao H 2013 Acta Phys. Sin. 62 163103
29Baluja K LTossell J A 2003 J. Phys. B: At. Mol. Opt. Phys. 36 19
30Fisher E RKickel B LArmentrout P B 1992 J. Chem. Phys. 97 4859
31Polak M LGilles M KLineberger W C 1992 J. Chem. Phys. 96 7191
32Peterson K AWoods R C 1990 J. Chem. Phys. 92 7412
33Midda SDas A K 2004 Int. J Quant. Chem. 98 447
34Werner H JKnowles P J 1988 J. Chem. Phys. 89 5803
35Werner H JKnowles P J 1985 J. Chem. Phys. 82 5053
36Werner H JKnowles P JKnizia Get al. MOLPRO (ver.2012.1), a Package of ab initio Programs
37Douglas MKroll N M 1974 Ann. Phys. 82 89
38Hess B A 1986 Phys. Rev. A 33 3742
39Peterson KAWoon D EDunning T HJr. 1994 J. Chem. Phys. 100 7410
40Feller D1992J. Chem. Phys.966104
41Li SZheng RChen S JFan Q C 2015 Mol. Phys. 113 1433
42Li SZheng RChen S JZhu D SFan Q C 2014 Spectrochim. Acta Part A 133 735
43Li SChen S JZhu D SFan Q C 2013 Comput. Theor. Chem. 1017 136
44Murrell J NSorbie K S 1974 J. Chem. Soc. Faraday Trans. 70 1552
45Le Roy R JLevel 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels
46Hotop HLineberger W C 1985 J. Phys. Chern. Ref. Data 14 731
47Blondel C 1995 Phys. Scr. T58 31
48Zhang Y PCheng C HKim J TStanojevic JEyler E E 2004 Phys. Rev. Lett. 92 203003
49Zhang Y PSong J PGan C LYan X ANie Z QJiang TLi LDu KZhang X CLu K QEyler E E 2006 Chin. Phys. 15 2288
50Zhang Y PGan C LSong J PYu X JMa R QGe HJiang TLu K QEyler E E 2005 Chin. Phys. Lett. 22 1114
51Zhang Y PGan C LSong J PYu X JGe HMa R QLi C SLu K QEyler E E 2005 Chin. Phys. Lett. 22 1110