Cite this Article
Zhang Hailong, Wang Enrong, Min Fuhong, Zhang Ning. Hysteresis-induced bifurcation and chaos in a magneto-rheological suspension system under external excitation. Chinese Physics B, 2016, 25(3): 030503  
Permissions
Hysteresis-induced bifurcation and chaos in a magneto-rheological suspension system under external excitation
Zhang Hailong1, 2, Wang Enrong2, Min Fuhong2, Zhang Ning1, †,
Magneto-electronic Laboratory, School of Physics and Technology, Nanjing Normal University, Nanjing 210046, China
Vibration Control Laboratory, School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China

 

† Corresponding author. E-mail: zhangning@njnu.edu.cn

Projects supported by the National Natural Science Foundation of China (Grant Nos. 51475246, 51277098, and 51075215), the Research Innovation Program for College Graduates of Jiangsu Province China (Grant No. KYLX15 0725), and the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20131402).

Abstract
Abstract

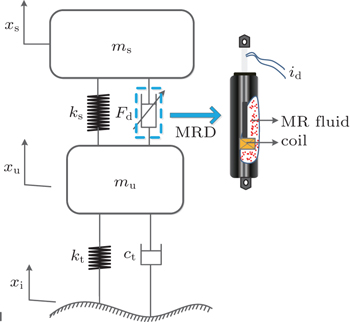
The magneto-rheological damper (MRD) is a promising device used in vehicle semi-active suspension systems, for its continuous adjustable damping output. However, the innate nonlinear hysteresis characteristic of MRD may cause the nonlinear behaviors. In this work, a two-degree-of-freedom (2-DOF) MR suspension system was established first, by employing the modified Bouc–Wen force–velocity (F–v) hysteretic model. The nonlinear dynamic response of the system was investigated under the external excitation of single-frequency harmonic and bandwidth-limited stochastic road surface. The largest Lyapunov exponent (LLE) was used to detect the chaotic area of the frequency and amplitude of harmonic excitation, and the bifurcation diagrams, time histories, phase portraits, and power spectrum density (PSD) diagrams were used to reveal the dynamic evolution process in detail. Moreover, the LLE and Kolmogorov entropy (K entropy) were used to identify whether the system response was random or chaotic under stochastic road surface. The results demonstrated that the complex dynamical behaviors occur under different external excitation conditions. The oscillating mechanism of alternating periodic oscillations, quasi-periodic oscillations, and chaotic oscillations was observed in detail. The chaotic regions revealed that chaotic motions may appear in conditions of mid-low frequency and large amplitude, as well as small amplitude and all frequency. The obtained parameter regions where the chaotic motions may appear are useful for design of structural parameters of the vibration isolation, and the optimization of control strategy for MR suspension system.

PACS: 05.45.–a;45.90.+t;05.45.Pq;46.15.–x;
Keyword:magneto-rheological damper;hysteresis;Bouc–Wen model;chaotic motions;
1. Introduction

Magneto-rheological fluids (MRFs) are known as smart materials, whose yield stress and viscosity can reversely change when subjected to or removed from a magnetic field.[1–4] The MR damper (MRD) utilizing MRF has highly controllable yield stress, which allows the MRD for the adaption to a wide range of shock loads and vibrations. Moreover, MRD possesses the characteristics of low power consumption and fast response, because the controllable output damping force can be easily achieved by adjusting the DC drive current. Therefore, MRDs have been widely used in the semi-active structural control applications.[5–8] However, like most of the advanced devices adopting smart materials (such as ionic polymer metal composites, piezoelectrics, and shape memory alloys), MRDs also exhibit hysteresis nonlinear properties. The multi-valued and non-smooth hysteresis will bring up many complex dynamical behaviors, such as bifurcation and chaos.[9,10] Walter[11] investigated the responses and codimension-one bifurcations in masing-type and Bouc–Wen hysteretic oscillators, and found a rich class of solutions and bifurcations mostly unexpected for the hysteretic loop. Lamarque[12] investigated the dynamics of energy harvesting systems with hysteresis and nonlinearity, where the hysteresis bifurcations were explained. Nicola[13] carried out the study on a short steel wire rope which exhibited the hysteresis, and found that the Neimark–Sacker bifurcations cause the loss of stability of the periodic response.

In engineering application, most effort was made on the semi-active control of MRDs, and the 2 degree of freedom (2-DOF) MR suspension system is a pervasive solution for the control strategy design. In Ref. [5], the skyhook semi-active controller, which was derived from the 2-DOF MR suspension model, was employed on a seat suspension for a helicopter crew seat. In Refs. [6] and [7], the 2-DOF MR suspension system was employed on the vehicle semi-active suspension system, to simultaneously satisfy the performance requirements of ride comfort and handling stability. However, there are few studies on the nonlinear dynamic behaviors caused by hysteresis, especially little on the 2-DOF MR suspension system. Raghavendra[14] examined the chaotic motion in a vehicle suspension system with hysteretic nonlinearity when excited by a road profile, thus establishing the limiting conditions of the MR suspension system. Luo et al.[15] modeled the 1-DOF semi-active MR suspension system through a piecewise-linear model. The mapping technique was employed to predict the periodic motions and bifurcation, and the periodic and stable motions were carried out. Krzysztof[16] proposed the nonlinear MR damping force by a hyperbolic tangential function, thereby building the MR damped Duffing system. Regions of stable or unstable solutions have been determined by a continuation method. Yan[17] investigated the effect of nonlinear damping suspension on the nonperiodic motions of a flexible rotor in journal bearings, and found more complicated nonlinear damping effects than those in the Duffing oscillators. Litak[18] investigated the chaotic motion in a hysteresis nonlinear vehicle suspension system, which was subjected to multi-frequency excitation, and found the critical amplitude of the road surface when the system vibrates chaotically. Nevertheless, the Bouc–Wen phenomenon model is a recognized model to describe MRDs, which accurately represents the inherent hysteresis nonlinear properties, compared with both a piecewise-linear model and the hyperbolic tangential model.[19] Though the Bouc–Wen model is widely used in practical application, the nonlinear dynamic analysis of MR suspension based on it is still rare. In addition, stability analysis under a random road spectrum is more practical and applicable, but it was ignored in the previous studies.

Due to the complex and nonlinear hysteretic characteristics of MRDs, intensive effort is required to reveal the unstable performance of MR suspension system. In this paper, nonlinear dynamic analysis of the MR suspension, modeled with the modified Bouc–Wen hysteresis MRD model, is conducted for the first time. To investigate the effect of excitation on non-periodic motions of the system, computational methods are used to solve the nonlinear dynamic equations of the system. Dynamic trajectories, bifurcation diagrams, and PSD diagrams are applied to analyze the effect of the properties of the excitation. The chaotic regions, including the range of amplitude and frequency are revealed under harmonic and random road surface.

2. Dynamical model of the MR suspension system

In Fig. 1, a classic dynamic model of 2-DOF MR suspension system, as well as the schematic diagram of MRD is presented.[20] Between them, only the MRD has strong force hysteresis and saturation nonlinearities. The other components are linearized. ms and mu are defined as the sprung and unsprung masses. ks, id, and Fd represent the suspension stiffness, DC drive current, and yielded damping force of the MRD, kt and ct denote equivalent stiffness and damping coefficient, and xi, xs, and xu are defined as the external excitation, vertical displacements of the sprung and unsprung masses, respectively. Following the principle of Newton’s Second Law of motion, the dynamic equation is formulated as[21,22]

Fig. 1. Schematic diagram of 2-DOF vehicle MR suspension system and MRD.

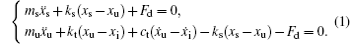
The conventional Bouc–Wen phenomenon model cannot show the nonlinear response and saturation characteristics of the magnetic field. Hence, sigmoid function has been proposed.[21] This issue is effectively solved by decoupling the hysteretic characteristics with the current modulation separation

where id and Im express the direct current and its maximum drive current, respectively, and 0 ≤ id ≤ Im, c(id) denotes the saturated nonlinear direct current control function proposed by the authors, Fh(xr, vr) denotes yielded passive damping force with hysteresis depending on the relative displacement velocity (vr) of the piston for id = 0. Here, xr is the piston travel of the MRD, which equals to xs–xu,

where c(id) ≥ 1, c(id) = 1, for id = 0, k2 and a0 are positive constants, I0 is an arbitrary constant, Fh(xr, vr) denotes yielded passive damping force with hysteresis depending on vr of the MRD for id = 0,

where c1 represents the viscous damping at low velocity, and k1 is the accumulator stiffness, x0 accounts for initial position of piston rod, and y is the internal displacement of the piston expressed as

where c0 and α are constants to describe the relationship with the applied voltage v, k0 is a constant to control the stiffness at large velocities, and z is the evolutionary variable without units, which is ruled by

where parameters γ, β, and A are constants to regulate the hysteresis loop, n describes the smoothness of the transition, the smaller of which the smoother the curve, and the typical value is n = 2.[20]

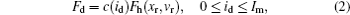
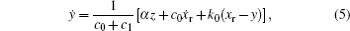
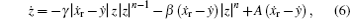
A CARRERA MagneShockTM MRD is further employed, which permits a maximum control direct current 0.5 A at 12 V. The MRD is tested in bench test according to the national standard, including schematics of damping force versus displacement of piston, damping force versus velocity of piston, etc.[8] The model parameters are identified based on tested data, as k0 = 184.1, k1 = 1528.1, k2 = 10.092, a0 = 7.526, I0 = 0.069, α = 20373.7, β = 233849.1, γ = 8816.9, c0 = 1368.7, c1 = 6222.7, n = 2, A = 20.6, x0 = −0.004. 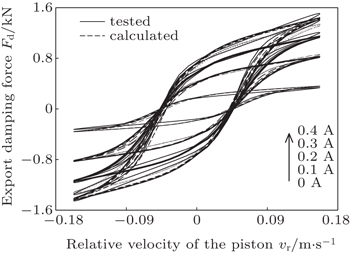Figure 2 shows the comparison of the modified Bouc–Wen hysteresis F–v model and the tested data of employed candidate MRD, under the harmonic excitation with amplitude 12.5 mm at 1.5 Hz and different driven current (0–0.4 A), which exhibits ideal coordination.

Fig. 2. Comparison of tested data and calculated results of the force–velocity curve at different current (0–0.4 A).

Apparently, MRD possesses a strong nonlinear property. Due to the damping force dependence of the driven current and excitation frequency, the F–v curve varies evidently under different driven and excitation profiles. As a result, nonlinear behaviors caused by hysteresis cannot be ignored in engineering application. In previous work, we concentrated on the semi-active control strategy of the MRD,[22–24] but ignored the potential nonlinear behaviors caused by hysteresis. To expose dynamical characteristics of the system essentially, the dimensionless numerical equations are expressed as follows, by choosing the independent parameters of ms and ks,

where

Here, x̃s, x̃u, and x̃i (τ) are the dimensionless quantities of displacement of sprung mass and unsprung mass, and external excitation, respectively. By setting x1 = x̃s, , x3 = x̃u, , equation (7) can be rewritten in the following differential equations:

3. Bifurcation and chaotic motions under external excitation

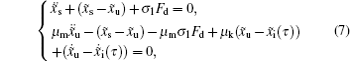
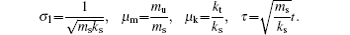
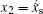
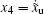
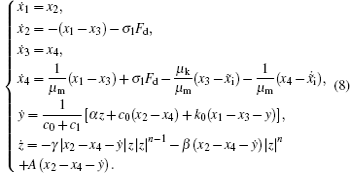
When there is no external input, namely, x̃i (τ) = 0, the dynamic system (8) has an obvious equilibrium point P = (0, 0, 0, 0, 0, 0). The Jacobian matrix of the system is given by

where

Parameters of the 2-DOF MR suspension system are selected based on an actual vehicle: ms = 562.5 kg, mu = 90 kg, ks = 57000 N/m, kt = 285000 N/m, and ct = 100 N/m·s−1.[22] The roots of the characteristic equation evaluated at equilibrium point P are λ1 = 93.1261, λ2 = −26.6980 + 44.4321i, λ3 = −26.6980-44.4321i, λ4 = −3.0854 +10.0483i, λ5 = −3.0854 − 10.0483i, λ6 = 0.0444. Apparently, P is a saddle point. Due to the unstable eigenvalues, the system may have chaotic motions.

In addition, the characters of the external excitation are the key influencing factor of the dynamical behaviors, thus deserve more attention.[25] According to the nonlinearity of the differential equations (8), the dynamic response of the mentioned model is studied numerically with the fourth-order Runge–Kutta algorithm. In the computation, the absolute error tolerance was set to be less than 10−6. Since numerical integration could give spurious results regarding the existence of chaos due to insufficient small time steps, the step size was verified to ensure no such results were generated as a result of time discretization. The initial condition is chosen as (0, 0, 0, 0, 0, 0). In this section, series of reliable numerical methods are used for investigating nonlinear dynamics, including the bifurcation diagram, LLE diagram, time history, phase portrait, and PSD diagram. The bifurcation diagram is obtained by use of the Poincare map. The LLE is obtained by applying the Wolf algorithm.[26]

3.1. Under harmonic excitation

Observation of the system response under harmonic input is the average method. Here, the most common excitation of the harmonic excitation is chosen, namely,

and the non-dimensional form is

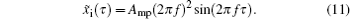
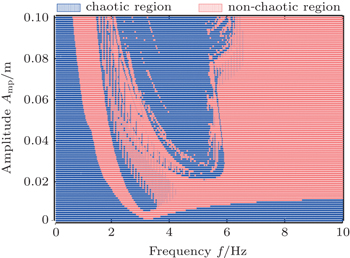
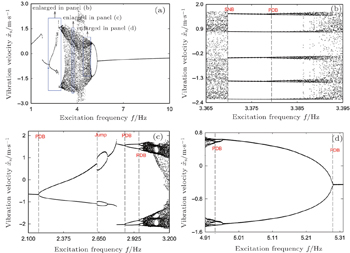
The two-parameter space plots are calculated to investigate the effects of the influence of external excitation on chaos. For each value of the varied parameter, the same initial conditions are used. In Fig. 3, the space plot of the frequency and amplitude of harmonic excitation is presented. The blue color indicates chaotic motions, estimated based on the LLE. In the chaotic region, all the LLEs are positive. As we can see, the chaotic motions principally distribute in four regions. Note, the chaotic and non-chaotic motions alternately appear in mid-frequency with larger amplitude, which indicates the complicated dynamic behaviors.

Fig. 3. Two parameters space plot: frequency versus amplitude of harmonic excitation.

To have better insight into the dynamic evolution process, and to verify the above parameter space plot, the bifurcation diagram under parameter variations is plotted. Figure 4 shows the bifurcation diagram, with excitation frequency f varying in the region of 1–10 Hz and amplitude fixed at 0.05 m. The bifurcation diagram is obtained by plotting the stroboscopic point of the vibration velocity ẋs. As shown in the global bifurcation diagram of Fig. 4(a), the complex dynamic behaviors are apparent for multi-line dots and nebulous dots, which indicate the quasi-period and chaotic motions, respectively. Local bifurcation diagrams are further plotted, particularly for regions of 2.1–3.2 Hz, 3.365–3.395 Hz, and 4.91–5.32 Hz. From Fig. 4(b), it is observed that the system response routes to chaos are from period and quasi-period by period-doubling bifurcation (PDB). The system keeps period-1 until 2.1881 Hz, and then turns to period-2. With frequency increasing to 2.6351 Hz, a jump phenomenon appears that the multi-line dots split from 2 to 4 discontinuously, which indicates the existence of the grazing bifurcation involved in period-doubling bifurcation.[27] The system returns to period-2 through inverse period-doubling soon at 2.7162 Hz. Yet again, the grazing behavior appears which leads the response to different period-2 orbits at 2.7932 Hz. Next, as the frequency continues to increase, chaotic motions occur through series period-doubling from period-2 to period-4, and to period-8. From Fig. 4(c), a saddle-node bifurcation (SNB) is observed. The system escapes from the chaotic attractors, turning into the periodic window of period-5 orbits, and returning to the chaotic region through transient period-doubling soon. As shown in Fig. 4(d), the system reverts to period-4 motion at 4.9383 Hz, next to period-2 motion through PDB. In the end, the single stable period motion occurs at 5.2896 Hz, through PDB from period-2.

Fig. 4. Global and partial enlarged bifurcation diagrams versus excitation frequency f, (a) global bifurcation diagram for 1–10 Hz with an increment step of 0.0001, (b) local bifurcation diagram for 2.1–3.2 Hz with an increment step of 0.0001, (c) local bifurcation diagram for 3.365–3.395 Hz with an increment step of 0.00001, (d) local bifurcation diagram for 4.91–5.31 Hz with an increment step of 0.0001.

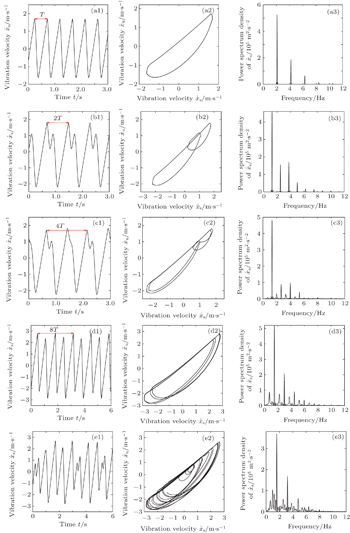
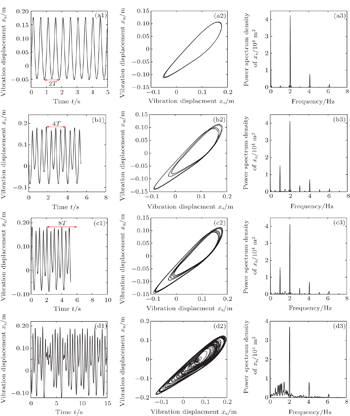
The time histories, phase portraits, and PSD diagrams of the system are depicted, to make a rather intuitive presentation of the dynamical behavior. The dynamical evolutions of the system are presented in Figs. 5–7, corresponding to Figs. 4(b)–4(d), respectively. As shown in Fig. 5(a), for 2.1005 Hz, the system exhibits as period-1 orbits, according to the periodic time series, single close-loop phase trajectory, and discrete PSD. With frequency increased, for 2.5025 Hz, 2.6795 Hz, and 2.9832 Hz, it is observed that the system suffers the period-doubling, from period-1 to period-8, with the increasing of the vibration amplitude. From phase trajectories shown in Figs. 5(a2)–5(e2), the number of loops doubles. In addition, the frequency multiplication is observed from PSD diagrams in Figs. 5(a3)–5(e3). In the end, as shown in Fig. 5(e), the chaotic attractor exists for 3.2 Hz. At this frequency, both the time series and phase trajectory are unordered, in addition, the PSD becomes continuous.

Fig. 5. Time series, phase portraits, and PSD for varying frequencies in the PDB corresponding to Fig. 4(b): (a1)–(a3) 2.1005 Hz, (b1)–(b3) 2.5025 Hz, (c1)–(c3) 2.6795 Hz, (d1)–(d3) 2.9832 Hz, and (e1)–(e3) 3.2 Hz.
Fig. 6. Time series, phase portraits, and PSD for varying frequencies in the periodic window of period-5 orbits corresponding to Fig. 4(c): (a1)–(a3) 3.37104 Hz, (b1)–(b3) 3.38529 Hz.
Fig. 7. Time series, phase portraits, and PSD for varying frequencies in the inverse PDB corresponding to Fig. 4(d): (a1)–(a3) 5.2255 Hz, (b1)–(b3) 5.2659 Hz.

The system escapes from the chaotic region by the SNB, which is shown from the bifurcation diagram in Fig. 4(c). As shown in Fig. 6(a), for 4.1201 Hz, period-5 motion exists after the system flees from the chaotic attractor. Through PDB, weak period-10 motion occurs. Comparing Fig. 6(a2) with Fig. 6(b2), it is found that the phase trajectory splits slightly, though maintaining the shape. After that, the system returns to a bigger chaos attractor, according to the amplitude of vibration.

Figure 7 shows the dynamical evolution of the inverse PDB corresponding to Fig. 4(d). With the frequency further increased, from Fig. 7(a), the system is running out of chaos again, and turning to period-2. After that, the system turns into period-1 orbits through inverse PDB, and becomes stable. The results are consistent with the bifurcation diagrams above.

Amplitude is another important parameter of excitation, which plays a critical role in the dynamic responses. Figures 8(a) and 8(b) show the global and partial enlarged bifurcation diagrams for amplitude Amp, varying from 0.005 m to 0.1 m. The frequency is set as middle-frequency of 4.1 Hz. It is observed that the system response enters chaos when amplitude increases, through the routes of PDB from period-1 to period-8 orbits. Combining the parameters space plot in Fig. 3, the LLEs of amplitude above 0.05 m are all positive, which verifies the chaos. Moreover, LLEs of amplitude near 0.0375 m are turned into negative unexpectedly. Note, dots in the bifurcation diagram near 0.0375 m are spiked suddenly, which indicates the new period-2 orbits. Here, only PDB occurs, unlike the evolution with frequency varying. The first bifurcation point is about 0.0296 m, and the system does not have a periodic window in the chaotic region.

Fig. 8. Global and partial enlarged bifurcation diagrams versus the excitation amplitude Amp: (a) global bifurcation diagram for 0.005–0.1 m with an increment step of 0.00001, (b) local bifurcation diagram for 0.041–0.049 m with an increment step of 0.000001.

Figure 9 expresses the time histories, phase portraits, and PSD diagrams corresponding to different Amp for 0.04372 m, 0.047245 m, 0.04793 m, and 0.0558 m, respectively. The process of PDB is confirmed from the multiple divisions of the phase plane, as well as from the frequency-doubling in PSD diagrams. For 0.04372 m, an indistinctive period-2 orbit occurs shown in Fig. 9(a1), which corresponds to the enlargement in the process of PDB shown in Fig. 8(a). Note, each bifurcation behavior shows subtle shifts of the original trajectories, from PSD diagrams in Figs. 9(b3) and 9(c3). Until the amplitude of external excitation is increased to 0.0558 m, just as shown in Fig. 9(d), the time series and phase trajectories become irregular, and the frequency spectrum becomes continuous, which is a presage of chaotic attractors.

Fig. 9. Time histories, phase portraits, and PSD for different Amp in the PDB: (a1)–(a3) 0.04372 m, (b1)–(b3) 0.047245 m, (c1)–(c3) 0.04793 m, and (d1)–(d3) 0.0558 m.
3.2. Under bounded stochastic excitation

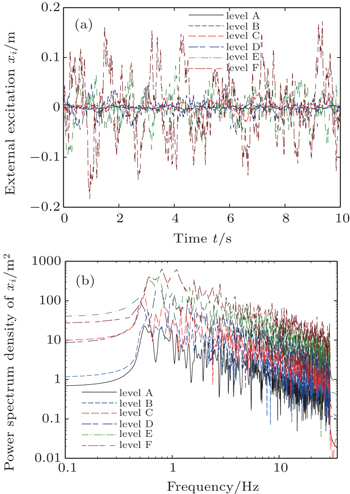
More generally, random excitation is the most common form of external disturbance for the vibration isolation system. Here, the bounded stochastic road spectrum is considered as the external excitation for MR suspension. The spectral density function of the road surface is first defined as follows:

where f denotes spatial frequency, which expresses the reciprocal of wavelength, f0 is the spatial frequency benchmark fixed at a constant as 0.1, v is the driving velocity, and ω is frequency index fixed as 2, Gq(f0) denotes the road surface spectrum value at f0. Further, the amplitude function of road surface is defined as follows:

Thus the external excitation is expressed as

and the non-dimensional form is

where N is the data length of the distributed time t, Δf is cell frequency calculated according to (fmax − fmin)/N, where fmax and fmin denote the maximum and minimum frequency components, respectively, and φ is a random phase obtained by rand[(0,2π), N], which illustrates the N random numbers in a range between 0 and 2π.

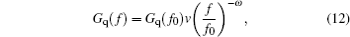
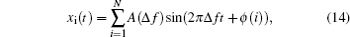
The parameters in this paper are given as: v = 30 km/h, fmin = 0.5 Hz, fmax = 30 Hz, and t = 10 s. The distributed time step is set as 0.0001 to avoid a shortage of storage space, then N is calculated at 100000. The road level is divided into six levels according to the different Gq(f0), and that is, level A corresponding to 16 × 10−6, level B corresponding to 64 × 10−6, level C corresponding to 256 × 10−6, level D corresponding to 1024 × 10−6, level E corresponding to 4096 × 10−6 and level F corresponding to 16384 × 10−6, respectively. Figure 10 shows the time history and the power spectrum density diagram of the external excitation of six levels. Level A is the smoothest, which is used to express well-paved road. From level A to F, the smoothness is getting worse, and level F expresses the worst rough road. Obviously, the amplitude is worsening from level A to F. On the other hand, all of the six levels cover the range of the actual road frequency distribution.

Fig. 10. Time history (a) and power spectrum density (b) of six levels of excitation.

Phase portraits of xs versus xu are plotted in Fig. 11, to observe the dynamic responses under the stochastic road. For six levels, the initial points are all selected at (0, 0, 0, 0, 0, 0), and the run time is set at 10 s so that the trajectory could fill the phase space as far as possible. The red arrow refers to the initial direction. As we can see from Fig. 11, the states of motion under level A, level B, and level C are similar, which have similar initial directions and orbits. What is more, the final destinations of all three levels converge to a limit area, observed from the cluster of the trajectory in Fig. 11; for levels D and E, apparently, the state of response of the system has changed. The initial direction of level D remains the same as that of the levels before, while the trajectory has changed soon after initial moving. For level D, the initial direction has changed to the opposite. In addition, the orbits of level D and level E evenly spread in the final destinations, unlike that of the levels before, which show the cluster of trajectory. As a consequence, the strange attractors are to be suspected to occur under level D and level E. Moreover, the orbit of the system under level F gets to be divergent, which indicates that the system becomes unstable.

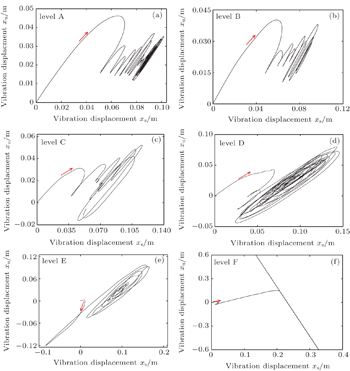Fig. 11. Phase portraits of different levels of road surface. Panels (a)–(f) correspond to levels A–F, respectively.

The LE is used again to determine the chaos. The C–C method is adopted to calculate the embedded dimension and delay time for phase space reconstruction, and after that, the LLEs under the six levels are obtained. Besides, Kolmogorov entropy (K entropy) is the effective evaluation index for distinguishing chaos from stochastic and stable state.[28] Thus, K entropies under the six levels are calculated by using the least square method. As is listed in Table 1, the response of the system is non-chaotic under level A, level B, and level C for the negative LLE. Meanwhile, the corresponding K entropy is infinite, which shows the stochastic response of the system in accordance with the input excitation. However, for levels D and E, the LLEs are becoming positive and the corresponding K entropy is rational positive, which indicate the chaotic motion. For level F, both LLE and K entropy become zero, and this indicates that the system is in an unstable state of divergence. LLEs and K entropies have good consistency with the above analysis of the phase portraits for the six levels.

Table 1.

Largest Lyapunov exponent and K entropy for different levels.

.
3.3. Discussion

These results are complete verification of the set of parameters where chaos may occur in MR suspension system under external excitation. For harmonic excitation, the frequency shows insensitive characteristics of mid-frequency of 3–5 Hz, where the chaotic motions and periodic windows exist alternately. Meanwhile, with the increase of amplitude, chaotic motions appear through the PDB. The threshold value is regular of around 0.03 m, thereby illustrating the great possibility of the appearance of chaotic motions in practical application. The chaotic area we obtained is consistent with that obtained in Ref. [15], which is also the low- and mid-frequency. What is more, the results here are more realistic, especially for the amplitude of chaotic motions, compared with that of exaggerated 0.36 m of the 1-DOF simplified model used in Ref. [18]. As for the random road surface, the larger the PSD of excitation, the more likely chaotic motions will occur in the MR suspension system. As shown in Figs. 4, 5, and 8, direct harm caused by chaotic motions is that the vibration amplitude increased nearly 50%, which may directly lead to the collapse of the vibration isolation system. In the event of the vehicle, it will threaten the passengers’ lives. Therefore, one should pay more attention to the responses of the middle-frequency for structural design of the vibration isolation with MRD, such as vehicle semi-active suspension system mentioned here. The results can be directly used as a reference in engineering application.

The analytic method used in this paper could be generalized to other nonlinear systems. That is, the global chaotic features analysis is first conducted by the two- or three-parameter plot based on LLEs with varying parameters. After that, the typical parameter domain is further studied thoroughly, to demonstrate the process of the nonlinear dynamic evolution. Meanwhile, the bandwidth-limited stochastic excitation used here can be used for nonlinear dynamic analysis on a non-autonomous system with the general external disturbance. Moreover, in this case, the K entropy is an effective and convenient means for distinguishing the chaos from stochastic.

As a note of caution, however, the integrated vehicle MR suspension system consists of four or more 2-DOF sub-systems used in this paper, which means that the dynamic model is with a higher DOF, and the nonlinear dynamic analysis of the system needs to be conducted. Moreover, the MR suspension system usually works with the semi-active mode. To reveal the nonlinear dynamic of semi-active MR suspension is the ultimate goal, while the passive current is used here for basic research.

4. Conclusions

The nonlinear dynamic responses of an MR suspension system were assessed with the methods of nonlinear dynamics. Various system responses for road parameters change (under the external excitation of harmonic and random road surface), such as time histories, bifurcation diagrams, phase planes, and PSD diagrams were observed using the 2-DOF MR suspension model with modified Bouc–Wen hysteretic MRD model. The result was a range of possible parameters of external excitation, where unstable responses existed. Under a single frequency harmonic excitation, the small amplitude is below about 0.005 m, and the middle-low frequency of 0.1–6 Hz is more likely to cause instability phenomena even chaos. In addition, chaotic motions are more likely to appear when riding through rough road surfaces. While riding through the relatively flat road surface, the vertical vibration of the MR suspension system is restricted within the limited state space. The obtained exact excitation profiles and chaotic regions in the paper may influence semi-active control strategies designed for the MR suspension system. The analysis may contribute to reliably implementing MRD to structural vibration semi-active control systems, and to researching the smart materials with hysteresis phenomenon and nonlinear characteristics. In the subsequent work, research on chaotic suppression and hardware experiments will be conducted.

Reference
1Park B JFang F FChoi H J 2010 Soft Mater. 6 5246
2Vicente J DKlingenberg D JHidalgo-Alvarez R 2011 Soft Mater. 7 3701
3Mclaughlin GHu WWereley N M 2014 J. App. Phys. 115 17B532
4Arash M KMehdi MSayad H 2014 J. Vib. Control 20 2221
5Hiemenz G JGregory JHu WWereley N M 2008 J. Aircr. 45 945
6Dong X MYu MLiao C RChen W M 2010 Nonlinear Dyn. 59 433
7Khiavi A MMirzaei MHajimohammadi S 2014 J. Vib. Control 20 2221
8Shin Y JYou W HHur H MPark J H 2014 Smart Mater. Struct. 23 095023
9Awrejcewicz JDzyubak L P 2005 J. Sound Vib. 284 513
10Baek S KMoon H T 2006 Phys. Lett. A 352 89
11Walter LFabrizio V 2003 Nonlinear Dyn. 32 235
12Lamarque C HSavadkoohi A TNaudan M 2013 Eur. Phys. J. Special Topics 222 1617
13Nicola CWalter LFabrizio V 2014 J. Sound Vib. 333 1302
14Naik R DSingru P M 2009 Mech. Res. Commun. 36 957
15Luo A C JRajendran A 2007 J. Vib. Control 13 687
16Krzysztof KAndrzej MDanuta SJerzy W 2014 Meccanica 49 1887
17Yan SDowell E HLin B 2014 Nonlinear Dyn. 78 1435
18Litak GBorowiec MMichael I FKazimierz S 2008 Commun. Nonlinear Sci. 13 1373
19Aurelio DIon SRamin S 2014 J. Intel. Mat. Syst. Str. 25 967
20Wang W JYing LWang E R 2009 J. Mech. Eng. 45 100 (in Chinese)
21Zhang H LWang E RZhang Net al. 2015 Chin. J. Mech. Eng. 28 63
22Zhang H LWang E RMin F Het al. 2013 Chin. J. Mech. Eng. 26 498
23Wang E RYing LWang W Jet al. 2008 Chin. J. Mech. Eng. 21 13
24Su M BRong H W 2011 Chin. Phys. B 20 060501
25Farshidianfar ASaghafi A 2014 Shock Vib. 2014 809739
26Wolf ASwift J BSwinney H Let al. 1985 Physica D 16 285
27Tian R LYang X WCao Q JWu Q L 2012 Chin. Phys. B 21 020503
28Cencini MFalcion MOlbrich EKantz HVulpiani A 2000 Phys. Rev. E 62 427