† Corresponding author. E-mail:
Project supported by the Earmarked Research Grant from the Research Grants Council of HKSAR, China (Grant No. CUHK 401212).
Fidelity measures the similarity between two states and is widely adapted by the condensed matter community as a probe of quantum phase transitions in many-body systems. Despite its success in witnessing quantum critical points, information about the fine structure of a quantum phase one can get from this approach is still limited. Here, we proposed a scheme called fidelity spectrum. By studying the fidelity spectrum, one can obtain information about the characteristics of a phase. In particular, we investigated the spectra in the one-dimensional transverse-field Ising model and the two-dimensional Kitaev model on a honeycomb lattice. It was found that the spectra have qualitative differences in the critical and non-critical regions of the two models. From the distributions of them, the dominating k modes in a particular phase could also be captured.
A quantum phase transition (QPT)[1,2] is driven by quantum fluctuations in the ground state of a many-body system. As an external parameter such as a magnetic field varies, the qualitative structure of the system's ground-state wavefunction exhibits an abrupt change across the quantum critical point. With this observation, researchers were motivated to use the fidelity, which is a concept borrowed from the quantum information theory, to study QPTs.[3,4]
Fidelity measures the similarity between two states. Mathematically, the static ground-state fidelity is defined as the magnitude of the overlap between two ground states differing from each other by a small value in the parameter space. Within one phase of the system, the two states have similar structures and thus the fidelity is close to unity. On the other hand, the ground states in distinct phases of the system are significantly different from each other. The fidelity is thus expected to show a sudden drop across the quantum critical point. The significance to use fidelity and its variations, such as fidelity susceptibility,[5,6] generalized fidelity susceptibility,[7] fidelity per site,[8,9] reduced fidelity,[10,11] operator fidelity,[12,13] and density-functional fidelity,[14] as a probe of QPTs have been testified in a number of condensed matter models (for a comprehensive review, please refer to Ref. [15]). Recently, an equality relating the fidelity susceptibility and the spectral function has been derived.[16] This makes the fidelity susceptibility to be directly measurable in experiments via neutron scattering or the angle-resolved photoemission spectroscopy (ARPES) techniques.
Although the fidelity can well witness a quantum critical point and provide us the critical exponents in continuous phase transitions,[17–20] the information about the nature and the symmetry of a phase that one could obtain is limited. With the motivation to gain more insight about a quantum phase from the fidelity approach, we proposed the fidelity spectrum in this work. Recently, Gu et al.[21] and Sacramento et al.[22] also introduced the concepts of mode fidelity and fidelity spectrum, respectively, with similar motivations.
In Sacramento and his collaborators' proposal, the fidelity spectrum was defined through the fidelity operator 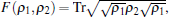
The paper is organized as follows. In Section 2, we established a general mathematical framework of the fidelity spectrum. The fidelity spectrum was studied in the 1D transverse-field Ising model, which exhibits a continuous QPT, and the honeycomb lattice Kitaev model, which exhibits a topological QPT. The results are discussed in Sections 3 and 4, respectively. Finally, a summary is given in Section 5.
Consider a general form of Hamiltonian,


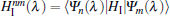
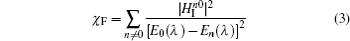
Consider the overlap




Physically, the fidelity spectrum tells us how much the ground state of the final Hamiltonian comes from different eigenstates of the initial Hamiltonian. When the system is under an external perturbation δλHI, the perturbed ground state is in general a superposition of the eigenstates of the unperturbed Hamiltonian. The contribution from the ground state is given by the fidelity while the contribution from the n-th excited state of the original Hamiltonian is governed by Mn. As one can see from Eq. (
To have a quantitative description of the distribution of {Mn}, we introduce a quantity
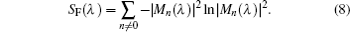
The 1D transverse-field Ising model is one of the simplest many-body systems, which is exactly solvable and exhibits a QPT.[27–31] The Hamiltonian of the model is given by
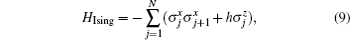
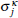
The model’s Hamiltonian can be diagonalized through standard procedure using the Jordan–Wigner transformation, Fourier transformation, and Bogoliubov transformation.[1] After these transformations, equation (
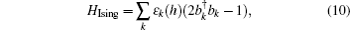
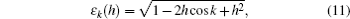
To investigate the fidelity spectrum in Eq. (
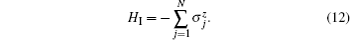

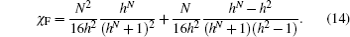
Figure
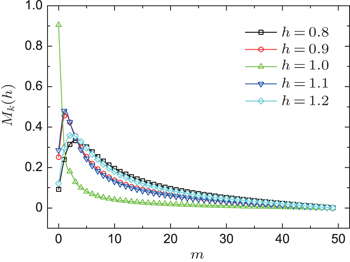 | Fig. 1. A plot of Mk in Eq. ( |
Quantitatively, we can also obtain the dominating mode by considering dMk/dk = 0 which gives cosk = 2h/(1 + h2). For h = 1, k = 0 is a solution to the equation. However, note that for N is even, k = (2m + 1)π/N and the k = 0 mode is not allowed in a finite system. Instead, Mk peaks at k = π/N, which in turn tends to zero as N tends to infinity.
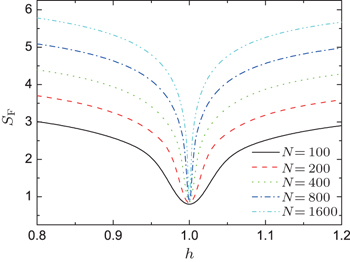
Figure
In addition, a point worth noting from the figure is that SF is insensitive to the system size at the critical point while it shows a non-trivial scaling behavior with N for h ≠ 1. For h = 1, the size dependence of SF can be obtained analytically. Putting Eq. (

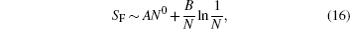
Figure
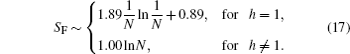
The Kitaev model was first introduced by Kitaev to study anyonic statistics.[36] The ground state of the model can be exactly obtained and it is found to possess a topological QPT.[36,37] Its ground-state phase diagram consists of gapless phases with non-Abelian anyon excitations and gapped phases with Abelian anyon excitations. As an exactly solvable 2D model exhibiting such an interesting phase diagram, the Kitaev model and its extensions have been intensively studied in the field of condensed matter physics (for examples, please see Refs. [38]–[42]). Besides, the model also captured much attention in the field of quantum information processing for its potential to realize the fault-tolerant quantum computation.[43]
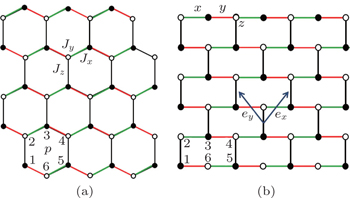
The model consists of 1/2 spins located at the vertices of a honeycomb lattice. They are interacting with the nearest neighbors through three types of bonds, namely, x, y, and z bond, depending on their directions (see Fig.
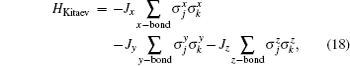
Consider the plaquette labeled as p in Fig. 
The Hamiltonian in Eq. (

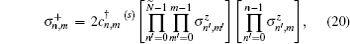

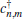
Introducing the Majorana fermion operators


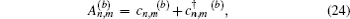
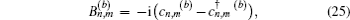

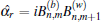
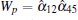

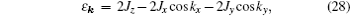
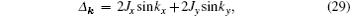
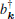
For
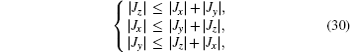
To calculate the ground-state fidelity spectrum, let us consider varying Jz along the Jx = Jy line on the Jx + Jy + Jz = 1 plane (see the red dashed line in the inset of Fig.

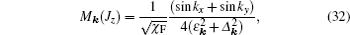

The distribution of
 | Fig. 5. 3D plots of the distributions of Mk over the k space for (a) Jz = 0.1, (b) 0.3, (c) 0.5, (d) 0.7, (e) 0.9 in the Kitaev model. Here kx = (2mx + 1)π/L and ky = (2my + 1)π/L, and L = 100. |
The behavior of the fidelity spectrum in the gapless phase of the Kitaev model is similar to that at the critical point of the Ising model in which the energy gap vanishes. When the system is gapless in the energy spectrum, the ground state is readily excited to other states. From the peaks in the fidelity spectrum, one can immediately realize which modes’ contributions are the largest for various values of Jz.
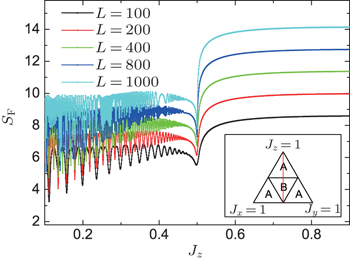
Figure
Moreover, SF in the gapless phase is an oscillating function of Jz. This feature comes from the periodic level-crossing occurred in the excited states of the system. The oscillation patterns are magnified in Fig.
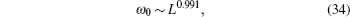
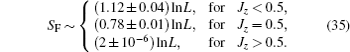
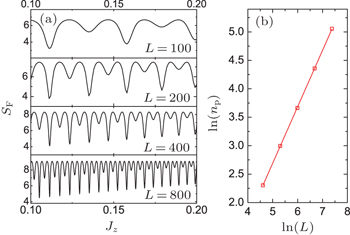 | Fig. 7. (a) Oscillating pattern of SF in the gapless phase. (b) Size dependence of the number of peaks (np) in SF in the gapless phase. The slope of the straight line is 0.991 ± 0.004. |
 | Fig. 8. Scaling behavior of SF for various values of Jz. The straight lines are the linear fitting of the data points. |
Interestingly, like the Ising model, the pre-factor of the size dependence of SF in the gapped region is also equal to unity. If we express the scaling behaviors in the two models both in terms of N, we have
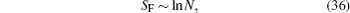
In summary, we investigated the fidelity spectra in the 1D transverse-field Ising model which exhibits a continuous QPT, and in the 2D honeycomb lattice Kitaev model which exhibits a topological QPT. We found that the fidelity spectrum shows qualitatively different behaviors in different phases of the model. A common feature about the spectrum is that the distribution is dominated by certain k modes in the gapless region while it is more dispersive in the gapped region.
To characterize the distribution of the fidelity spectrum quantitatively, we introduced the quantity SF in analogy to the Shannon entropy. It was found that at the critical point of the Ising model, SF ∼ ln N/N while it scales with lnN in the non-critical region. The latter scaling behavior also holds for the Kitaev model. The universality of the relation in Eq. (
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 |