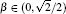† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474168 and 61401222), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20151502), the Qing Lan Project in Jiangsu Province, China, the Natural Science Foundation of Jiangsu Higher Education Institutions, China (Grant No. 15KJA120002), and the Priority Academic Development Program of Jiangsu Higher Education Institutions, China.
Hybrid entangled state (HES) is a new type of entanglement, which combines the advantages of an entangled polarization state and an entangled coherent state. HES is widely discussed in the applications of quantum communication and computation. In this paper, we propose three entanglement concentration protocols (ECPs) for Bell-type HES, W-type HES, and cluster-type HES, respectively. After performing these ECPs, we can obtain the maximally entangled HES with some success probability. All the ECPs exploit the single coherent state to complete the concentration. These protocols are based on the linear optics, which are feasible in future experiments.
Quantum entanglement is a significant physical resource which plays a fundamental role in many meaningful applications of quantum information processing.[1] For example, quantum entanglement can be used in quantum teleportation,[2] quantum key distribution,[3] quantum secure direct communication,[4,5] and some other important quantum communication protocols.[6–18] Hence, entanglement is considered to be the information carrier in quantum information and should be created first.
Typically, there are two types of entanglements. The first one is encoded in discrete variables, such as horizontal and vertical polarization states of photons.[19] The second one is encoded in continuous variables, such as the entangled coherent state (ECS).[20] In recent years, there is another type of entanglement which has been widely studied. It is the hybrid entanglement.[21–29] The hybrid entangled state (HES) means that the entanglement is generated between different degrees of freedom of a particle pair. In 2006, van Loock et al. proposed the first hybrid quantum repeater protocol using bright coherent light.[21] In 2013, Sheng et al. first discussed the entanglement purification for the hybrid entangled state.[26] Recently, an important work about the generation of a hybrid entangled state was reported.[27] Interestingly, Lee and Jeong put forward a new type of hybrid entanglement.[28] Based on the HES, they proposed near-deterministic quantum teleportation and resource-efficient quantum computation. In their protocol, a qubit is encoded in the combination of polarization states and coherent states. The orthogonal basis to define an optical hybrid qubit is {|0L〉 = |+〉|α〉, |1L〉 = |−〉|−α〉}, where 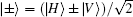
In quantum communication protocols, the quantum channel must be maximally entangled. Unfortunately, the maximally entangled states usually collapse into nonmaximally entangled states or even mixed states because of the imperfect channel in the practical process of storage and transmission. In order to obtain the high quality and secure quantum communication, we should first repair the degraded quantum entanglement channel. Entanglement concentration is an important method that we can distill the maximally entangled states from the less-entangled states.[30] In 1996, Bennett et al. proposed the first entanglement concentration protocol (ECP) with collective measurement, which is based on the Schimidt decomposition.[30] Until now, many ECPs have been proposed.[30–80] For example, Zhao et al. proposed ECPs based on the linear optical element.[33] In 2008, Sheng et al. presented a recyclable ECP based on cross-Kerr nonlinearities[34] and the efficiency of their protocol was improved obviously. In 2012, Sheng and Deng first presented the basic principle of efficient single-photon-assisted ECP for partially entangled photon pairs.[35,36] Subsequently, with the help of the single qubit, the ECPs for arbitrary W states,[51–62] cluster states,[63–69] cat states,[71] χ type entangled states,[72] hyper-entangled states,[74–77] and hybrid entangled states[78] were also proposed.
In this paper, we will focus on the entanglement of the HES, which has the different form of Ref. [78]. We propose three ECPs for different types of HESs. The first ECP is to concentrate the Bell-type HES. The second and the third ECPs are to concentrate the W-type and the cluster-type HES, respectively. In the first ECP, we exploit an ancillary single coherent state and use the beam splitter (BS) to complete the task. In the second ECP, we require two coherent states, and in the third ECP, we require a single coherent state and a pair of ECS to realize the concentration. All protocols are based on the linear optics, which makes them feasible in future experiments.
This paper is organized as follows. In Section 2, we will describe the ECP for an arbitrary less-entangled Bell-type HES. In Section 3, we will propose the ECP for an arbitrary less-entangled W-type HES. In Section 4, we will discuss the ECP for an arbitrary less-entangled cluster-type HES. In Section 5, we will present a discussion.
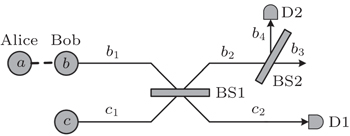
As shown in Fig.

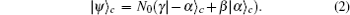
Therefore, the whole system can be written as
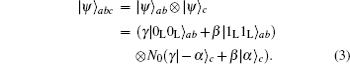
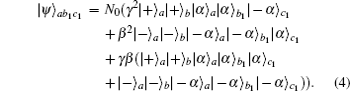
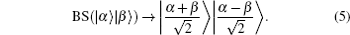
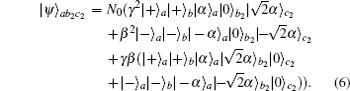
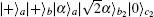

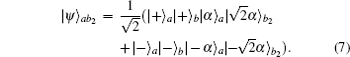
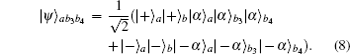
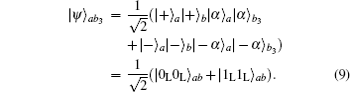
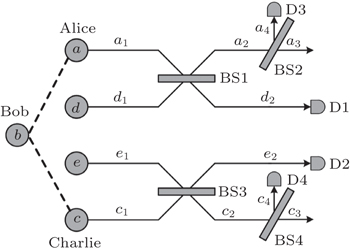
In this section, we will extend the above protocol to the case of arbitrary W-type HES of the form
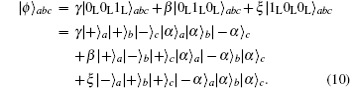
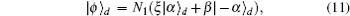
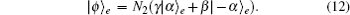
From Fig.
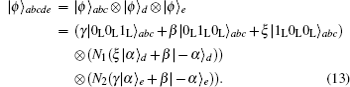
Then they let the coherent states in spatial modes a1, d1, e1, and c1 pass through the BSs, respectively. Therefore, the whole system can be rewritten as
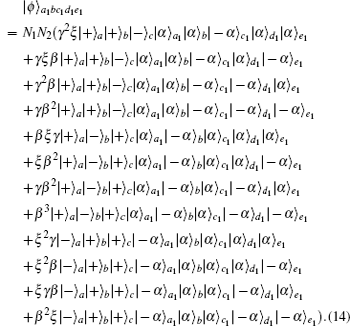
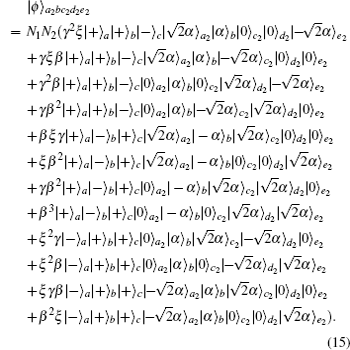

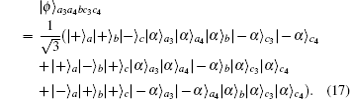

In this section, we will discuss the ECP for the cluster-type HES, where the initial less-entangled HES can be written as
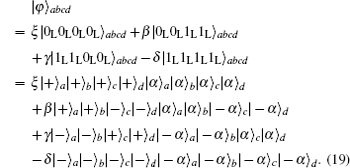
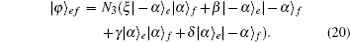
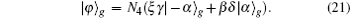
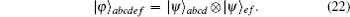
Schematic diagram showing the principle of the ECP for cluster-type HES. Alice, Bob, Charlie, and Dick share the HES, and own the hybrid qubits a, b, c, and d, respectively.
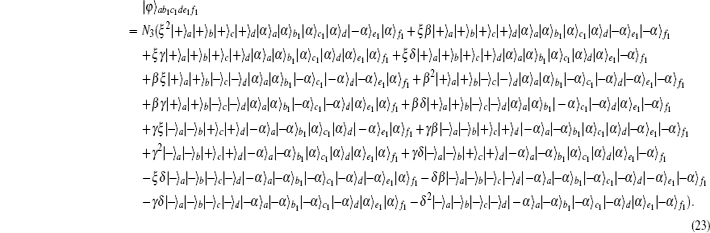
As shown in Fig.
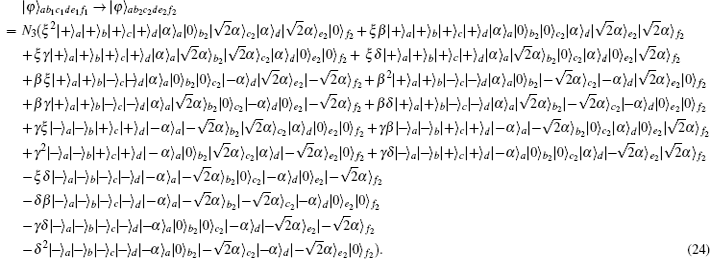
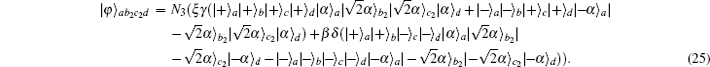

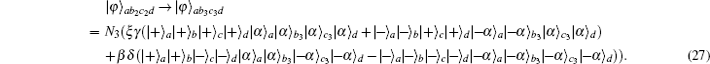
In the second step, they first prepare the ancillary single coherent state in spatial mode g as shown in Eq. (

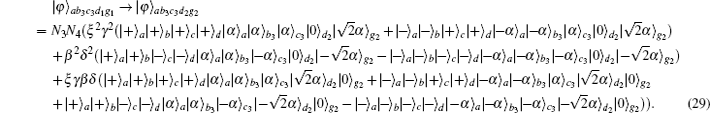
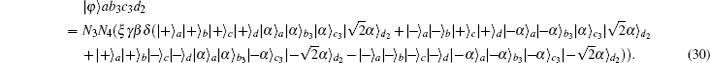
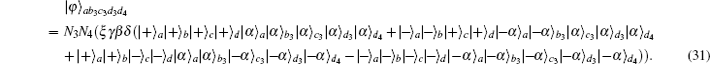
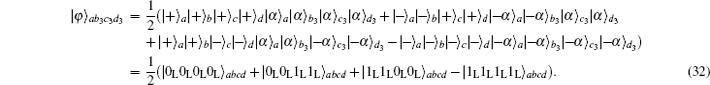
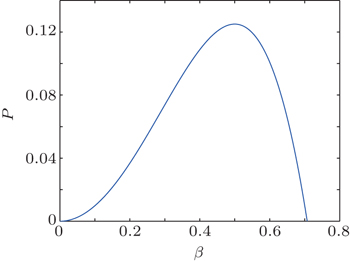
The success probability to obtain the maximally entangled HES from the initial partially entangled state is P3 = 4|N3N4ξγβδ|2.
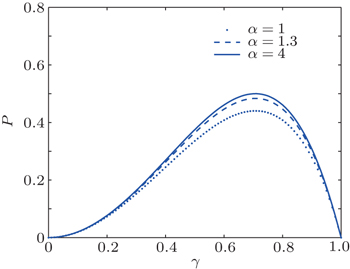
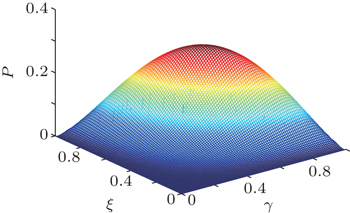
Thus far, we have described our protocols which mainly use BS and QND to complete the task. We described the ECPs for Bell-type HES, W-type HES, and cluster-type HES, respectively. With the post-section principle, we can ultimately obtain a maximally entangled HES with some probability. In Figs.
In Fig. 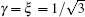
In our ECPs, the BS plays a key role to realize the concentration. We take the first ECP for example. As shown in Fig.
We have proposed three ECPs for three types of HES, respectively. First, we described the ECP for the Bell-type HES with arbitrary coefficients, and the probability of the ECP is 2|N0γβ|2. Second, we introduced the ECP for the W-type HES. We used two single coherent states to obtain the maximally entangled W-type HES with the probability of 3|N1N2γβξ|2. Finally, we described the ECP for the cluster-type HES. With the help of a pair of auxiliary particles of ECS and an auxiliary single coherent state, we obtained the maximally entangled cluster-type HES, and this ECP has a success probability 4|N3N4ξγβδ|2. These ECPs are all based on the linear optics which is feasible in future experiments. We hope that these ECPs based on HESs are useful in many applications of quantum information.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 |