† Corresponding author. E-mail:
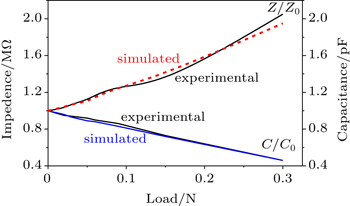
In this paper, the fabrication and investigation of flexible impedance and capacitive tensile load sensors based on carbon nanotube (CNT) composite are reported. On thin rubber substrates, CNTs are deposited from suspension in water and pressed at elevated temperature. It is found that the fabricated load cells are highly sensitive to the applied mechanical force with good repeatability. The increase in impedance of the cells is observed to be 2.0 times while the decrease in the capacitance is found to be 2.1 times as applied force increases up to 0.3 N. The average impedance and capacitive sensitivity of the cell are equal to 3.4 N−1 and 1.8 N−1, respectively. Experimental results are compared with the simulated values, and they show that they are in reasonable agreement with each other.
Since last decade, nanomaterials have been intensively investigated and used for various electronic sensors. In particular, single-walled carbon nanotubes (SWNTs), double-walled carbon nanotubes (DWNTs), and multi-walled carbon nanotubes (MWNTs) have been investigated for numerous types of sensors.[1–6] Several studies of carbon nanotube (CNT) applications[7–11] have proven that they are very favorable for organic electronics due to their flexibilities. For instance, in Ref. [12] it was described that how the miniaturized flexible temperature sensors based on polymer compositions filled with multiwalled carbon nanotubes were successfully fabricated. It was also found that CNTs behave as a semiconductor. The surface-type Al/CNTs/Al flexible temperature sensors have been reported in Ref. [13], where the resistance-temperature relationship has shown semi conductive behavior. The average temperature sensitivity of the sample was found to be (−1.26) %·°C−1. Recently, researchers have also been investigating electromechanical sensors based on CNTs and organic materials composite.[14] In Ref. [15], the recent development in the field of CNT/polymer nanocomposite based strain sensors has been reported. It has been shown that how these sensors are highly sensitive due to the specific conductivities of the composites, in particular, as a result of the presence of the internal conductive network formed by CNTs and tunneling effect of the transfer of charges. It was also shown by Shang et al.[16] that MWNTs and polyurethane can be used for fabricating the elastic conductive nanocomposite. The conductivity of the composite under uniaxial stretch up to 100% did not show significant variation which in turn, is rather unusual for this type of composite. On the other hand, for the case of the devices based on CNT composite, resistive type of sensor is commonly studied. Unlike the resistive sensors, impedance and capacitive sensors exhibit higher stability. In this paper, the fabrication and properties of flexible CNT-rubber composite impedance and capacitive tensile load cells are reported. The aim of this work is to develop a cheep, sensitive and stable tensile sensor using CNTs.
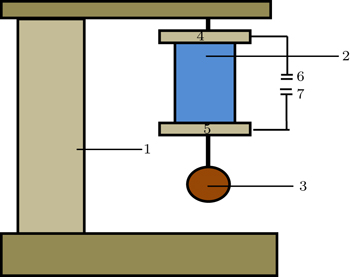
Commercially produced (Sun Nanotech Co Ltd., China) CNT powder was deposited on a thin flexible rubber substrate. The diameter of multi-walled nanotube (MWNT) was in a range of 10 nm–30 nm. The thickness of the commercially available flexible rubber substrate was equal to 80 μm; the dimensions of substrate were around (7 × 5) mm2. Using 5 wt% suspension of the CNT powder in water, the CNTs were deposited on the rubber substrate. Once the CNT film on the rubber substrate dried on one side, then the CNT film was deposited on the opposite side of the substrate. Before deposition of thin film, suspension was stirred for a few minutes. The samples were then pressed at pressures ranging from 4 kN·m−2 to 6 kN·m−2 and temperatures of around 90 °C–110 °C for 1 min–2 min. Figure
Figure
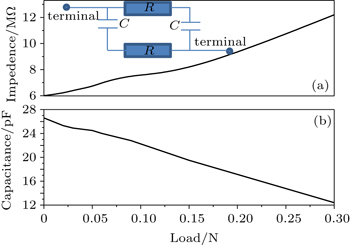
Figure
As observed in Fig.
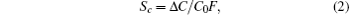

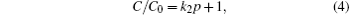
In the study by Yasuoka et al.,[24] the employment of carbon nanofiber (CNF) and elastomer composite as resistive strain gauge sensing device has shown a promising potential due to its decent flexibility, and conductivity. The device is sensitive enough and exceeds the conventional measurement limit of 40% strain deformation. Besides, it can offer wider applications due to the virtue of its flexibility thus it is much favorable for measuring flexible materials. Meanwhile, Manandhar et al.,[25] have reported the application of wet hydrogel based strain gauge which can measure up to 25% of strain, and its gauge factor was found to be near 2. The presence of carbon filling and conducting polymer coating further enhances the sensing performance, so that it exhibits no relaxation nor hysteresis effect. However, still, it encounters some problems such as the drifting effect which could be avoided only through proper encapsulation and installation of the electrical wiring connection due to the soft nature of the aerogel. A study to investigate the flexible large strain gauge sensor from polypyrrole on rubber substrate was carried out by Tjahyono et al.[26] The sensor was reported to have good stability and consistency, with a gauge factor of 1.86. The consistency of the device is associated with the careful control of the extension and contraction of the air muscle with a PID controller. On the other hand, a simple, flexible, and highly sensitive strain gauge sensor was developed by Pang et al..[27] through using a method of reversible interlocking of nanofibers. The sensor is sensitive enough to detect changes in pressure, shear, and torsion force with gauge factors of 11.5, 0.75, and 8.53 respectively. These properties, thus, make it have potential applications such as artificial skin attachable sensor. The sensor also has a highly repeatable response of up to 104 cycles, and excellent switching characteristics. In comparison, we report on the fabrication and investigation of flexible capacitive and resistive mechanical sensing device based on carbon nanotube (CNT) composite. The device has shown good sensitivity and good repeatability in response to the applied force of up to 0.3 N. The changes in both impedance and capacitance are measured to be factors of 2.0 and 2.1 with gauge factors of 2.0 and −1.1, respectively.
The investigation of the properties of the flexible impedance and capacitive tensile load cells based on CNT composites shows that the cells are very sensitive to the force and has good repeatability. The impedance of the cells is observed to increase 2.0 times on average and the capacitance decreases 2.1 times by increasing the force up to 0.3 N. The experimental results are compared with the simulated ones, showing that they are in reasonable consistence with each other. The decrease of the conduction of the CNT-rubber composite under the effect of the tensile load is explained by percolation theory. The decrease of the capacitance of the sample under the effect of the tensile force is also explained by the possible decrease of dielectric permittivity of the CNT-rubber composite under the effect of the strain.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |