Cite this Article
Liu Xin, Guo Jin-Chuan, Lei Yao-Hu, Li Ji, Niu Han-Ben. Simple phase extraction in x-ray differential phase contrast imaging. Chinese Physics B, 2016, 25(2): 028704  
Permissions
Simple phase extraction in x-ray differential phase contrast imaging
Liu Xin†, , Guo Jin-Chuan, Lei Yao-Hu, Li Ji, Niu Han-Ben
Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, College of Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China

 

† Corresponding author. E-mail: sblx@szu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61101175, 61571305, and 61227802).

Abstract
Abstract

A fast and simple method to extract phase-contrast images from interferograms is proposed, and its effectiveness is demonstrated through simulation and experiment. For x-ray differential phase contrast imaging, a strong attenuation signal acts as an overwhelming background intensity that obscures the weak phase signal so that no obvious phase-gradient information is detectable in the raw image. By subtracting one interferogram from another, chosen at particular intervals, the phase signal can be isolated and magnified.

PACS: 87.59.–e;07.60.Ly;42.30.Rx;87.57.–s;
Keyword:x-ray imaging;x-ray interferometry;Talbot and self-imaging effects;phase contrast imaging;
1. Introduction

X-ray phase-sensitive technique is an important extension of x-ray radiographic imaging that is widely used in medicine, nondestructive testing, and security. Besides conventional absorption images, phase-sensitive imaging can offer two other images: phase distribution and dark field distribution.[1–4] Various phase-sensitive techniques have been proposed and developed over the past decade.[5–21] Among them, the differential phase contrast (DPC) imaging can be used in a broad range of applications due to its low requirements for source coherence, mechanical stability and detector resolution.[6]

Without specimen, interferograms of phase gratings consist of many regular fringes. An object introduced in the light path distorts the fringes, and the resulting variations in the intensity pattern encode the wavefront phase. The obtaining of the phase distribution of the sample requires a phase retrieval procedure that calculates the phase image from multiple intensity measurements. In the visible light region, Fourier-transform and phase-stepping algorithms are common phase retrieval methods.[8,9] Naturally, those techniques were introduced in DPC imaging system and yielded excellent results[8,10,11] No less than three images are needed for a phase-stepping algorithm; usually, the number of intensity measurements is in a range of 5 ∼ 11.[12] Multiple exposures cause excess exposure time and increased x-ray absorption, which are disadvantageous in medical and biological applications. Bennett et al. proposed a fast and simple algorithm that requires no movement of the grating.[10] However, it requires individual harmonic spectrum, resulting in the loss of high spatial frequency.

In this paper, we deduce the intensity distribution in a detecting plane for a finite-size x-ray source. The formula of intensity shows that the analysis grating parameters and x-ray source spatial coherence have the greatest effects on phase signals. The attenuation signals have more contributions than the phase shift signals in intensity image. Thus, usable phase information requires a map of phase retrieval. We propose a fast and simple method based on the intensity formula to extract the phase-gradient signals from the raw data without losing the high spatial frequency. Relative numerical calculations and experimental results demonstrate our method effectiveness.

2. Theoretical background

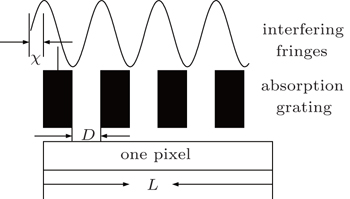
We consider a common x-ray interferometer with a finite-size x-ray source as shown in Fig. 1, where R and l denote the distances between the source grating (G0) and phase grating (G1), which is downstream of the sample, and between G1 and the analysis grating (G2), respectively. First, we consider only a monochromatic point x-ray source of wavelength λ, then we extend the result to a multi-slit x-ray source.

Fig. 1. X-ray differential phase contrast imaging and coordinate system.
2.1. Spherical wave source

The complex transmission function T(x) of G1 can be expressed with a Fourier series as

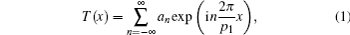
where an is the amplitude of the n-th harmonic and p1 is the period of the grating. At a distance l downstream of G1, the complex amplitude of the propagating field is given by

by using the paraxial approximation and a spherical beam illumination of G1, where λ is the x-ray wavelength and M = (R + l)/R is the magnification. For R ≫ l, M ≈ 1; hence, the phase factor of Eq. (2) is negligible. Then

When a sample is placed just before G1, G1 will split the incident light carrying the complex amplitude of the sample into different diffraction orders. As a consequence, the amplitude transmission function of the sample A(x,y)eiϕ(x,y) is shifted by ns along the x-axis, such that

where the shearing amount is s = lλ/p1. Therefore, from Eq. (4), the intensity I(x,y;l) = U(x,y;l)U* (x,y;l) is given by

where the superscript “*” denotes the conjugate, and

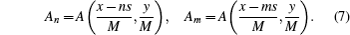
Assuming that the shearing amount ns is sufficiently small,[5] equations (5) and (7) respectively become

2.2. Multi-slit x-ray source

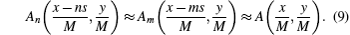
According to the van Cittert–Zernike theorem, the intensity distribution of a source will smoothen the interferogram I(x,y;l), so in the detecting plane, the intensity I′(x,y;l) is calculated as[15]

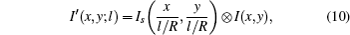
where Is(x,y) denotes the source intensity, which is the convolution of rectangle function rect(x/a) with a sum of delta functions,

The multi-slit source has periodicity p0 and the slit width α, as illustrated in Fig. 1.

2.3. Intensity distribution

The final intensity distribution on the detector is determined by taking into account the effect of the third grating G2 with periodicity p2. Assuming that G1 and G2 are parallel, the intensity signal detected by one pixel, according to the model in Fig. 2, is

where the relative position between x-ray fringes and G2 is χ, G2 has 100% absorption efficiency, the aperture width of one periodicity is D, and one pixel can collect k periodicities of x-ray fringes.

Fig. 2. Detection model of x-ray interfering fringes.

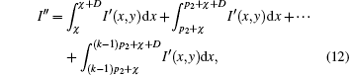
The signal I″ would be a very complex expression if we implement Eq. (4), (10), and (11) into Eq. (12) without any approximations. Using the special structure of G1 at the Talbot distance, we can obtain a compact expression of I″. For example, when the duty cycle of G1 is 0.5 and the imaging distance of G1 satisfies

and the intensity signal I(x,y;l) in Eq. (5) is given by

where only the 0, ±1 diffraction orders are considered, θ denotes the phase shift of G1, and p2 = Mp1/2. We assume that A(x,y)eiϕ(x,y) varies slowly with x, so the effect of convolving A(x,y) with ϕ(x,y) in Eq. (10) can be neglected.[15] That is to say, we neglect the scatting contribution to the intensity distribution I(x,y;l). The same assumption in Eq. (12) results in the integral

where

and sin cx = sin πx/πx. At the same time, G1 is located at special positon such that

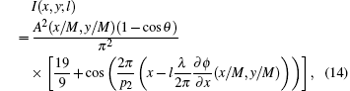
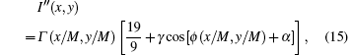
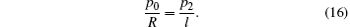
Now we can discuss the contributions of A(x,y) and ϕ(x,y) to the intensity signal I″(x,y). The value of γ determines the contribution of A(x,y) and small apertures of G0 and G2 can increase the occupancy rate of ϕ(x,y) in I″(x,y). However, a and D cannot be very small. In general, we choose parameters such that half the incident light passes though G0 and G2, which means that a/p0 = D/p2 = 0.5 and γ ≈ 0.4. Thus, the phase information amplitude only contributes 15% of the measured intensity, and most energy is attributed to the attenuation term Γ(x,y). The phase contrast signals, which provide more structural information, are consequently hard to detect for the attenuation signal.

3. Method

We estimate the values of ϕ(x,y) and A2(x,y) from the following equations:

where δ is the real part of the complex refractive index and μ is the quality factor of the attenuation. For light material, δ is typically on the order of 10−6–10−7 for 20 keV–30 keV x-rays, so that ϕ(x,y) is usually quite small(a few arc seconds), except is areas near edges and boundaries. We assume again that ϕ(x,y) varies slowly varying spatially and is sufficiently small so that equation (13) can be expanded and approximated as[15]

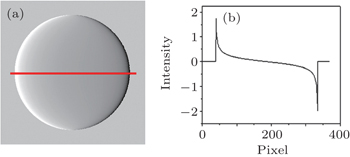
If the strong background signal Γ(x,y) can be eliminated from Eq. (19), the image intensity would be proportional to ϕ(x,y). A simple approach can delete this background signal by using only two raw images. A first interferogram is collected with the phase grating at α, and a second is obtained by moving the phase grating to α + π. Subtracting from results in

where k1 and k2 are constants that do not affect image contrast. Since ϕ(x,y) of an object is generally a spatially random distribution, we can reasonably expect

where ⟨·⟩ indicates the average over the entire intensity image. Thus, the k2 can be estimated and removed from the I″. On the boundaries, due to the large gradient, equation (20) can be rewritten as

which means that the signal intensity is not equal to the gradient of the phase. Nevertheless, since all edges are described by the same expression, I‴ can still give structural information. Our simple method removes the background signals and isolates phase signals.

4. Simulation and experiment
4.1. Numerical calculation

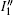
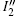
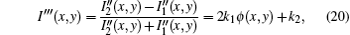
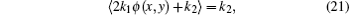
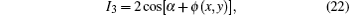
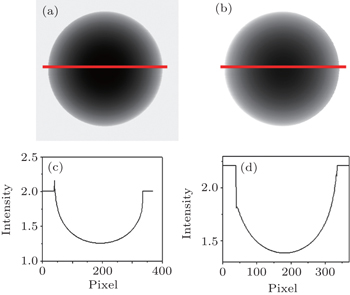
In this section, we show the results of numerical calculations of one carbon ball on the basis of Eqs. (4), (10), and (12).

Figures 3(a) and 3(b) are the raw images with the G1 placed at different positions, and figures 3(c) and 3(d) are the intensity profiles along the red bars, respectively. The following parameters are used in this simulation: λ = 0.041 nm, 1-mm carbon ball diameter, δ = 5.2 × 10−6, μ = 0.584 cm−1, p1 = 5.6 μm, l = 105 mm, R = 1470 mm, p0 = 42 μm, p2 = 3 μm, and 27-μm pixels. Except in the line profiles in Figs. 3(c) and 3(d), it is hard to find the gradient signal of phase. Using Eq. (20), we obtain the image of phase gradient image shown in Fig. 4.

Fig. 3. Raw intensity measurements of a carbon ball. The positions of G1 are α and α + π in panels (a) and (b), respectively. The line profiles in panels (a) and (b) correspond to the red lines in panels (a) and (b), respectively.
Fig. 4. (a) Phase-gradient image and (b) line profile corresponding to red line in panel (a).
4.2. Experiments

A fresh pig foot purchased from a supermarket was imaged using a non-absorption grating imaging system described in Ref. [14]. Two raw data images and a phase gradient image are shown in Figs. 5 and 6(a), respectively. It is difficult to visually distinguish the two raw images in Figs. 5(a) and 5(b). However, the phase gradient intensity profile of Fig. 6(b) shows the fine distinction caused by the phase shift. After removing the attenuation information using our method, the phase-gradient is detectable in the intensity distribution (Fig. 6(a)).

Fig. 5. Radiography images: panels (a) and (b) are raw images collected with the phase grating at two different positions.
Fig. 6. (a) Phase-gredient images calculated from the raw images of Fig. 5. The structures of trabeculae clearly emerge in the phase contrast, while they are invisible in Fig. 5. (b) Intensity profiles along the black lines in Figs. 5(a), 5(b), and 6(a). The curve at the bottom is a detailed part of the profile. Figures 5(a), 5(b), and 6(a) have the same scale bar.

The x-ray source is a common x-ray tube with no filter, at a 70-kV acceleration voltage, and with a 2-mA anode current. The distance between sample and detector is 105 mm. The phase grating is made of silicon, has a 5.6-μm period, a 0.5-duty ratio, and a 40-μm depth, corresponding to a π phase shift for 31-keV x-rays. The scintillator is directly coupled with an ANDOR 2048×2048-pixel (13.5 μm/pixel) CCD camera through a fiber optical tape, with 2× demagnification.

5. Conclusions

We present intensity formulae for x-ray Talbot interferometry with a partial spatial coherent source. On the basis of these formulae, we find that the structural parameters of the source and analyzer gratings greatly affect the phase-gradient signal intensity. For G0 and G2, a larger aperture in one periodicity dramatically reduces the amplitude of phase information to the extent that the phase-gradient image is difficult to detect in raw data. We propose a simple approach to extracting the phase image from raw signals and demonstrate its effectiveness through numeral calculation and experiment. Compared with the existing stepping methods using no less than three interferograms, our method is simpler and much faster.

Reference
1Momose ATakeda TItai YHirano K 1996 Nat. Med. 2 473
2Davis T JGao DGureyev T EStevenson A WWilkins S W 1995 Nature 373 595
3Wilkins S WGureyev T EGao DPogany AStevenson W 1996 Nature 384 335
4Wang S HMargie P OMomose AHan H JHu R FWang Z LGao KZhang KZhu P PWu Z Y 2015 Chin. Phys. B 24 068703
5Momose AKawamoto SKoyama IHamaishi YTakai KSuzuki Y 2003 Jpn. J. Appl. Phys. 42 L866
6Weitkamp TDiaz ADavid CPfeiffer FStampanoni MCloetens PZiegler E2005Opt. Express13
7Revol VKottler CKaufmann RStraumann UUrban C 2010 Rev. Sci. Instrum. 81 073709
8Takeda MIna HKobayashi S 1982 J. Opt. Soc. Am. 72 156
9Schofield M AZhua Y 2003 Opt. Lett. 28 1194
10Bennett EKopace RStein FWen H 2010 Med. Phys. 37 6047
11Wen HBennett EKopace RStein FPai V 2010 Opt. Lett. 35 1932
12Pfeiffer FBech MBunk OKraf t PEikenberry E FBronnimann CGrunzweig CDavid C 2008 Nat. Mater. 7 134
13Zhu PZhang KWang ZLiu YLiu XWu ZMcDonald S AMarone FStampanoni M 2010 Proc. Natl. Acad. Sci. USA 107 13576
14Du YLiu XLei Y HGuo J CNiu H B 2011 Opt. Express 19 22669
15Yashiro WMomose A 2015 Opt. Express 23 9233
16Kim JLee S WCho G 2014 Nucl. Instrum. Methods A: Accelerators, Spectrometers, Detectors and Associated Equipment 746 26
17Modregger PRutishauser SMeiser JDavid CStampanoni M 2014 Appl. Phys. Lett. 105 024102
18Peter SModregger PFix M KVolken WFrei DManserd PStampanoni M 2014 J. Synchro. Rad. 21 613
19Huang J HDu YLei Y HLiu XGuo J CNiu H B 2014 Acta Phys. Sin. 63 168702 (in Chinese)
20Zhang X DXia C JXiao X HWang Y J 2014 Chin. Phys. B 23 044501
21Han YLi LYan BXi X QHu G E 2015 Acta Phys. Sin. 64 058704 (in Chinese)