† Corresponding author. E-mail:
The propagation of narrow packets of electromagnetic waves (EMWs) in frequency dispersive medium with the consideration of the complex refractive index is studied. It is shown that counting in the dispersion of the complex refractive index within the context of the conventional expression of the group velocity of narrow wave packets of EMWs propagating in a dispersive medium results in the appearance of additional constraints on the group velocity, which dictates that the physically acceptable group velocity can only be realized in the case of a negligible imaginary part of the group index. In this paper, the conditions that allow one to realize the physically acceptable group velocity are formulated and analyzed numerically for the relevant model of the refractive index of a system of two-level atoms in the optical frequency range. It is shown that in the frequency band where superluminal light propagation is expected, there is a strong dispersion of the refractive index that is accompanied with strong absorption, resulting in a strongly attenuated superluminal light.
The studies of superluminal, backward, and slow narrow packets of light waves propagating in different media in the frequency range of strong dispersion of the refractive index have a long history.[1] Currently, the question on the existence, physical meanings, and potential consequences of such waves has become a hot research topic and sometimes controversial. In this respect, there are two groups of researchers: those who support the existence of superluminal electromagnetic waves[2] and those who reject such reports on grounds that it contradicts the special theory of relativity and consequently the so-called superluminal light has no physical meaning.[3] In 1970 it was reported in Ref. [4] that Gaussian packets of electromagnetic waves can travel in dispersive media with group velocity exceeding the velocity of light in a vacuum with no restrictions whatsoever. Recently, the topic has been discussed theoretically in many papers again and even some have reported on the experimental realization of such waves in strongly dispersive media.[2–12]
On the other hand, others have the view that the appearance of superluminal and negative group velocities of light cannot be attributed to a physical flow in the so-called superluminal region where there is strong dispersion of the refractive index that is accompanied by strong absorption.[13–15] H. Tanka, et al. obtained negative group velocity as well as pulse velocity (group velocity) that can exceed the speed of light in a vacuum in Rb vapor, however they showed that at the frequency band where this velocity is attained the intensity of the transmitted pulse is reduced by strong dispersion and consequently concluded that the observed velocity is not the velocity of energy flow, i.e., group velocity.[14] Similarly, it is reported that an electromagnetic wave (EMW) packet may travel at a superluminal velocity as well as negative group velocity, however the information carried by them is not superluminally transmitted and the information velocity carried by the wave front is still positive.[16]
The interesting topic that needs further discussion concerns the superluminal light with group velocity Vg exceeding the speed of light in a vacuum. Such a value of Vg is commonly obtained with the help of the conventional formula that does not take into account the dispersion of the imaginary part of the refractive index. In this paper, we consider the evolutions of narrow packets of electromagnetic waves with the consideration of the dispersion of the complex refractive index n(ω). It is shown that this dispersion significantly distorts the shape of the Gaussian wave packet, which is demonstrated by introducing the imaginary part of the group index ng2 along with the conventional real group index ng1.[5] The latter completely controls the group velocity with the help of the real part of n(ω) and its derivative with respect to the frequency ω. Our theoretical and numerical analyses show that the physically consistent group velocity Vg for a narrow packet of EMW can only be realized in the frequency bands where ng2 ≪ ng1. By considering the relevant model of the complex refractive index of an assembly of two-level atoms, it is shown that in the frequency bands where the conventional formula of Vg gives the superluminal group velocity, the condition ng2 ≪ ng1 is violated, confirming the fact that |Vg| > c has no physical meaning.
The rest of this paper is organized as follows. Section 2 is devoted to the study of the propagation of narrow packets of electromagnetic waves with the consideration of the dispersion of the imaginary part of the refractive index and the conditions on which the physically consistent group velocity can be realized are introduced. In Section 3, we consider the group indices and group velocity of light in an assembly of two-level atoms and determine the frequency bands where the physically acceptable group velocity is attained. The conclusions that are withdrawn from the results obtained in the paper are summarized in Section 4.
The profile of a Gaussian wave packet as a function of position x and time t propagating in a medium with dispersion can be obtained using the following equation:

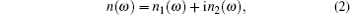
For the realistic expressions of n(ω) and arbitrary σ, the integration in Eq. (
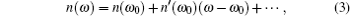

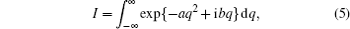
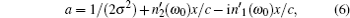
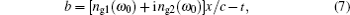
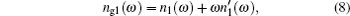
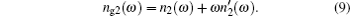
Equation (
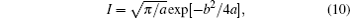
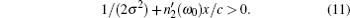
Basically, equation (
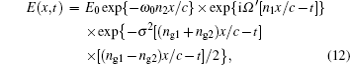
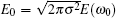
Let us compare Eq. (
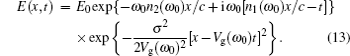

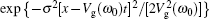
However, the consideration of the dispersion of the imaginary part of the refractive index n2(ω) considerably changes this picture. Let us rewrite the last exponent in Eq. (
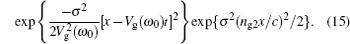
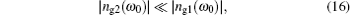
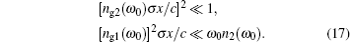
Equation (
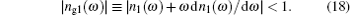
In the next sections we focus on the consistency of Eqs. (
Let us consider a system consisting of weakly interacting two-level atoms with the bottom and upper levels represented by a and b, respectively. The refractive index of such weakly interacting two-level atoms is given by
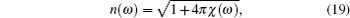
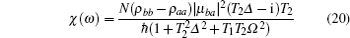

Below, we consider an equilibrium case when ρbb = 0 and ρaa = 1, that is, when the upper level is not populated. In the case of |χ| ≪ 1, which is consistent with the model, using Eqs. (
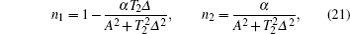
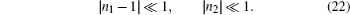
The real and imaginary parts of the group index ng are obtained with the help of Eqs. (
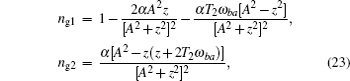
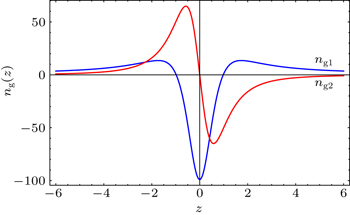
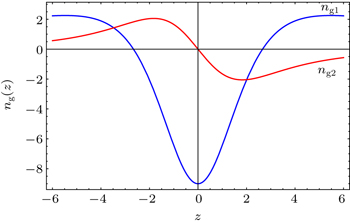
The frequencies in the vicinity of the resonance z = 0 are more interesting. To analyze the group indices in Eq. (
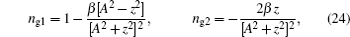
Figures
Figure
Figure
It is necessary to note that again in the vicinity of the resonance z = 0, equation (
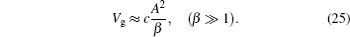
The profile of a narrow wave packet propagating in a dispersive medium is analyzed with the help of the standard procedure but with the consideration of the dispersion of the imaginary part of the refractive index. In addition to the conventional group index ng1, it contains a new expression ng2, which corresponds to the imaginary part of the complex group index. This quantity significantly changes the profile of the wave packet compared with the conventional case, with ng2 = 0.
The main result of the paper is that the group velocity calculated using the conventional formula Vg = c/ng1 has the physically acceptable value only for frequency ω, where |ng2(ω)| ≪ |ng1(ω)|. We verify the validity of this inequality with the help of the refractive index of a typical two-level atom model at optical frequency for the equilibrium case and show that it is violated for the frequency range where the conventional formula of Vg gives superluminal group velocity |Vg| > c. That is, in the frequency domain where superluminal light is expected, the presence of strong absorption attenuates the wave and makes it impossible to realize the physical superluminal light.
On the other hand, in the vicinity of the resonant frequency where the imaginary part of the refractive index of an equilibrium system is large and results in strong absorption, the imaginary group index ng2 ≈ 0, which allows one to realize the physically consistent group velocity corresponding to the slow negative light with negative real group index |ng1| ≫ 1.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |