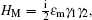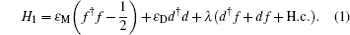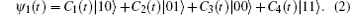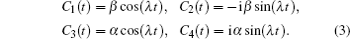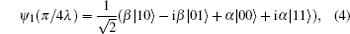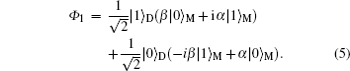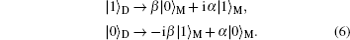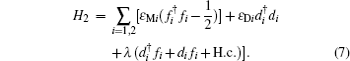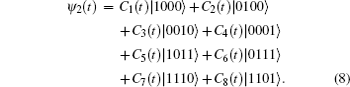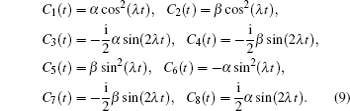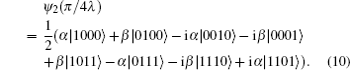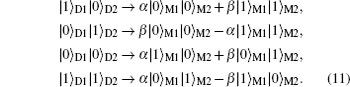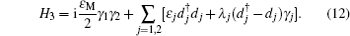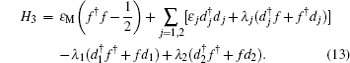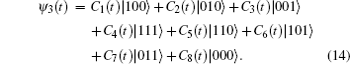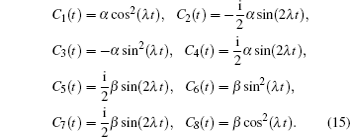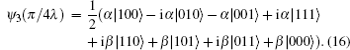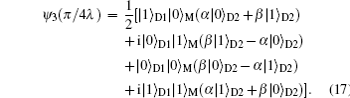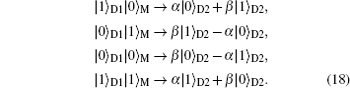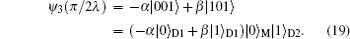1. IntroductionTopologically ordered systems provide a promising platform for quantum computation, where quantum information can be encoded in non-local degrees of freedom. This way of storing information is intrinsically robust against local sources of decoherence,[1] thus it is anticipated to overcome the limitations of decoherence in conventional quantum information processing. However, it is more difficult for manipulation and readout of quantum information hidden in the topological systems, compared with quantum conventional ones (e.g., ions, spins, photon polarizations, quantum dot charge qubits, superconducting qubits, etc.). Meanwhile conventional systems for quantum information process have achieved a lot of important progress, and have been intensively studied. In order to harness the relative strength of each kind of system, it would be highly desirable to realize quantum information transfer between conventional and topological quantum systems in a hybrid system.[2,3] In Ref. [2], a scheme to realize information transfer between topological and quantum dot (QD) charge qubits is proposed by using an ancilliary superconducting flux qubit as a medium; and in Ref. [3], a method was given for information transfer between topological qubits and QD spin qubits through adiabatically tuning the chemical potential of the quantum dot. While the above methods may play important roles, but during the exploratory stage, new practical and efficient proposals are still in high demanded.
In this paper, we propose a way to realize quantum information transfer between topological and QD charge qubits. The typical part in our suggested set up is sketched in Fig. 1, where a quantum dot (QD) is tunnel-coupled to a semiconductor Majorana-hosted nanowire (MNW).[4,5] Our method uses gated control as a switch for electron tunneling between the MNWs and QDs. Quantum information transfer between them can be realized by choosing the proper interaction time to make selective measurements, in this way, we have proposed an experimental scheme to probe the nonlocality of Majorana fermions.[6] We also realize long distance quantum information transfer between two quantum dots separated by the nanowire. Furthermore we analyze the teleportationlike electron transfer phenomenon predicted by Tewari et al.[7] in our considered system. Interestingly, we find this phenomenon exactly corresponding to the case that the information encoded in the electron state of one QD just returns back to its original place from the perspective of quantum state transfer.
2. The model and Hamiltonian of the typical hybrid setupThis typical hybrid system includes an MNW and a QD, for the MNW subsystem, where a one-dimensional spin–orbit coupling nanowire is in proximity with an s-wave superconductor. Being subject to a proper magnetic field, the nanowire is predicted to be driven into a topological superconducting phase with the right combination of spin–orbit coupling and induced superconductivity.[4,5] A pair of Majorana fermions (MFs) denoted by γ1 and γ2 are anticipated to appear at the two ends of the nanowire. The Hamiltonian of the paired MFs is described by 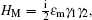 here εm ∼ e–L/ξ describes the overlap interacting strength of the two MFs. This inter-MF coupling damps exponentially with L (the length of the nanowire) and ξ (the superconducting coherent length). The two separated MFs can form one Majorana fermionic level, which can be either occupied or empty, and thus defines a nonlocal qubit.[8] We introduce a quantum dot tunnel-coupled to one of the paired MFs. The energy levels of QD are set in the Coulomb blockade regime, so that only one electron is allowed therein when the tunneling process takes place. The Hamiltonian of the quantum dot is described by HD = εDd†d, here d† and d are respectively the electron creation and annihilation operators of the dot, with the corresponding energy εD. The tunneling Hamiltonian between the QD and one of the paired MFs is described by HT = λ(d† − d)γ1, here λ is their tunnel coupling amplitude. The tunnel-coupling strength can be controlled by tuning the electrode gate voltage, in this way we can realize a switch to “turn on (off)” the tunnel-coupling connection. In addition, we will also need to measure the occupation situation of quantum dot or topological system. As to the quantum dot system, these kinds of measurements have been well developed in experiments via using a single-electron transistor[9] or quantum-point-contact (QPC) detectors.[10] While for the topological systems, different proposals have been suggested to carry out such measurements depending on the concrete realization, see Refs. [1], [11]–[14].
here εm ∼ e–L/ξ describes the overlap interacting strength of the two MFs. This inter-MF coupling damps exponentially with L (the length of the nanowire) and ξ (the superconducting coherent length). The two separated MFs can form one Majorana fermionic level, which can be either occupied or empty, and thus defines a nonlocal qubit.[8] We introduce a quantum dot tunnel-coupled to one of the paired MFs. The energy levels of QD are set in the Coulomb blockade regime, so that only one electron is allowed therein when the tunneling process takes place. The Hamiltonian of the quantum dot is described by HD = εDd†d, here d† and d are respectively the electron creation and annihilation operators of the dot, with the corresponding energy εD. The tunneling Hamiltonian between the QD and one of the paired MFs is described by HT = λ(d† − d)γ1, here λ is their tunnel coupling amplitude. The tunnel-coupling strength can be controlled by tuning the electrode gate voltage, in this way we can realize a switch to “turn on (off)” the tunnel-coupling connection. In addition, we will also need to measure the occupation situation of quantum dot or topological system. As to the quantum dot system, these kinds of measurements have been well developed in experiments via using a single-electron transistor[9] or quantum-point-contact (QPC) detectors.[10] While for the topological systems, different proposals have been suggested to carry out such measurements depending on the concrete realization, see Refs. [1], [11]–[14].
The total Hamiltonian of the system is a sum of the above three parts: H1 = HM + HD + HT. For practical calculations, it is more convenient to convert from the Majorana representation to the ordinary fermion one via the transformations: γ1 = i(f – f†), and γ2 = f + f†, where f is the ordinary fermion operator, satisfying the anticommutation relation {f, f†} = 1. After an additional local gauge transformation d → id, in the new representation, the total Hamiltonian of the system becomes[4,15]
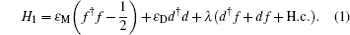
One may notice that the particle number in the system is not conserved, a pair of electrons can be extracted out from the superconductor and can be absorbed by the condensate. In this article, we assume
εM → 0, which corresponds to a long nanowire comparing with the superconducting coherent length. We also assume
εD = 0, which is in alignment with the degeneracy energy level of the topological qubit.
3. Information transfer between a quantum dot and a semiconductor Majorana-hosted nanowireWe first consider the typical system introduced in Section 2 to realize information transfer between a QD and an MNW. Associated with the above Hamiltonian Eq. (1), we introduce the state basis as |nD,nM〉, where nD,M = 0 or 1 denote the electron occupation number in the relevant QD energy level and the nonlocal level of the paired MFs. The combined initial state of the system is expressed as ψ1(0) = α|0,0〉 + β|1,0〉, which means that the quantum dot stays initially in a superposition state ψD(0) = α|0〉D + β|1〉D, with α and β encoding the information of the state, while the state of the paired MFs is empty. Starting from the initial state, the dynamical state of the whole system can be evaluated as
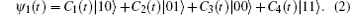
Inserting the above equation into the time-dependent Schrödinger equation, we get the solution as follows:
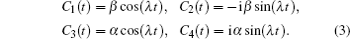
When the evolution time satisfied the condition
λt =
π/4, we turn off the connection between the QD and the MNW, which can be realized by tuning the gate that can control the coupling between them. We thus obtain the state
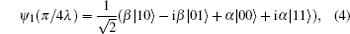
the above state can be transformed in such an equivalent form
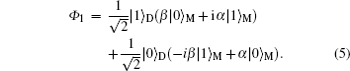
From the above equation, we can clearly see if we make a measurement on the electron occupation number of the dot, no matter what measurement results, empty or occupied, the total wave function will collapse onto the superposition empty and occupied state of the nonlocal fermion level, which contains the initial information of the quantum dot. The corresponding relations between the measurement results and the collapsed state of MFs are listed as follows
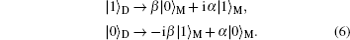
The above results show that the information (
α and
β) encoded initially in charge occupation state of the QD has been transferred to the nonlocal feimion level defined by the paired MFs. Following the same way, we can also transmit the information from the MNW to the QD inversely. Comparing the measurement of the occupation state of the quantum dot, the measurement of the paired MFs is more difficult, but different proposals have been suggested to carry out such measurements.
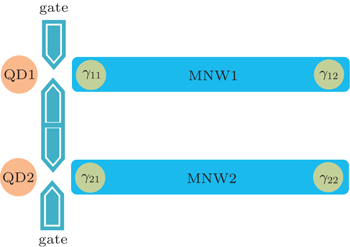
[1,11–14]3.1. Entanglement information transfer between double quantum dots and double MNWsCharge qubit defined in double quantum dots has been investigated in both theory[16] and experiment,[17] it can be regarded as a single-particle entanglement.[18,19] So we will investigate the system, as figure 2 shows, a double quantum dot is tunnel-coupled to double individual nanowires. We can transfer the entanglement information from the double quantum dots to the double MNWs, which also provides a way to prepare the entanglement state of two topological qubits by cloning the entanglement state of the double quantum dots. The Hamiltonian of the system is given by
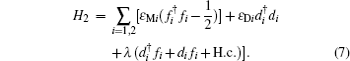
Associated with the above Hamiltonian, we introduce the state basis as |
nD1,
nD2,
nM1,
nM2〉, where
nD1,
nD2,
nM1,
nM2 denote, respectively, the occupation number (“0” or “1”) of the relevant energy level in QD1, QD2, MNW1, and MNW2. We assume the initial state of the two quantum dots as
ΨDD(0) =
α|1〉
D1|0〉
D2 +
β|0〉
D1|1〉
D2, and the initial state of the two paired MFs is unoccupied. The initial state of the two quantum dots is apparently a single particle (electron) entanglement state,
[18,19] containing the quantum information with coefficients
α and
β.
Starting from the initial state, we will consider the entanglement information transfer from the double QDs to the double MNWs. The dynamical state of the total system is expressed in a general form
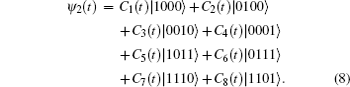
Inserting the above equation into the time-dependent Schrödinger equation, we get the coupled first-order differential equations for the probability amplitudes
Ci(
t) (
i = 1,2,…,7). Considering the specified initial condition, we get the solution as follows:
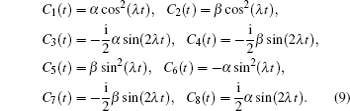
When the envolution time satisfied the condition
λt =
π/4, we can get the state
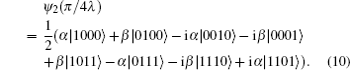
Then we make measurements on the electron occupation of the quantum dots. Depending on the different measurement results, there are four possible results, the relations are shown as follows:
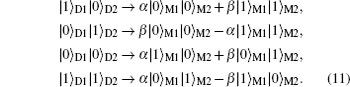
From the above relations, we can clearly see that no matter whatever measurement results, the initial entanglement information can be transferred to the double MNWs. According to the parity of the total occupation electron measured in QDs, the measurement results can be classed into two categories, even parity (only one electron), and odd parity (no electron or two-electrons occupation). Because of the parity conservation in the total system, we also notice that the two categories measurement results (even parity and odd parity) correspond to two kinds of entanglement forms (a superposition state of |0〉
M1|0〉
M2 and |1〉
M1|1〉
M2 and a superposition state of |0〉
M1|1〉
M2 and |1〉
M1|0〉
M2) respectively.
3.2. The quantum state teleportation between two separated quantum dots through the nonlocal paired MFsIn this section, as figure 3 schematically shows, we adopt such a system, where the two MFs, generated at the ends of the MNW, are tunnel-coupled to two QDs (i.e., QD1 and QD2) respectively. The total Hamiltonian of the system is described as follows:
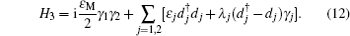
For practical calculations, the Hamiltonian of the system is transformed from the Majorana representation to the ordinary fermion one in the same way as mentioned in Section 2 and re-expressed as
[12]
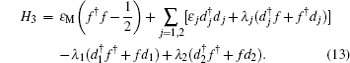
The Hamiltonian
H3 can be solved in the space spanned by the basis state |
n1,
nM,
n2〉, where
n1(2) and
nM denote, respectively, the electron occupation number (“0” or “1”) in the left (right) dot and the central MNW. Thus we have eight basis states totally, which can be divided into two subspaces: |100〉, |010〉, |001〉, |111〉 with odd parity; |110〉, |101〉, |011〉, |000〉 with even parity. For simplicity, we assume
λ1 =
λ2 =
λ and
εM =
ε1 =
ε2 = 0.
Tewari et al. analyzed an equivalent system in Ref. [7], assumed an extra single electron initially in one QD and stated that the electron can be transferred to the other quantum dot through a pair of nonlocal MFs occurring in a two-dimensional chiral p-wave superconductor. Corresponding to the “dot–MNW–dot” system we considered, it means, in a“long-wire” limit, the electron can transmit through the nanowire on a short timescale, showing thus a “teleportation” phenomenon. In Ref. [20], this interesting behavior has been investigated, stating that the real electron transfer did not occur in space. This excluded the possibility of superluminal electron transfer between the two remote quantum dots, this phenomenon is only the consequence of the Majorana’s nonlocality nature. In fact, the well-known quantum teleportation means to teleport an unknown quantum state from one object to the other through the formation of entangled links between remote locations. In this section, we study the “dot–MNW–dot” system to realize transfer of an unknown quantum state from one quantum dot to the other quantum dot far away via the nonlocal paired MFs and further talk about the “teleportationlike” electron transfer phenomenon from the perspective of quantum information transfer.
We assume the initial state ψ3(0) = α|1,0,0〉 + β|0,0,0〉, this means that the left dot stays in a superposition state ψ3D(0) = α|1〉 + β|0〉, with α and β encoding the information, while the right dot and the central MNW stay in an empty state initially. The dynamical state of the system can be evaluated as
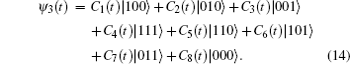
Considering the initial condition, we get the results through solving the Schrödinger equation as follows:
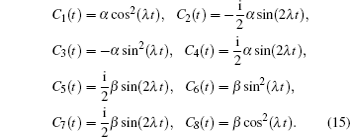
Choosing the proper interaction time, we can prepare the state needed for further analyses. When the envolution time satisfies the condition
λt =
π/4, from Eq. (
14) and Eq. (
15), we can get the state as follows:
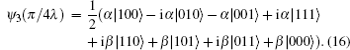
We rearrange the above equation in a different form, we can get
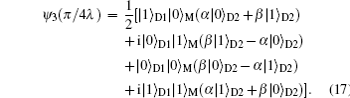
From the above equation, if we measure the electron occupation states in the relevant energy level of the QD1 and the nonlocal fermionic level of the MNW, no matter whatever the outcome of the measurement, the information transfer can be realized from one quantum dot to the other quantum dot far apart, the corresponding relations between the measurement results and the collapsed state of the right dot are listed as follows:
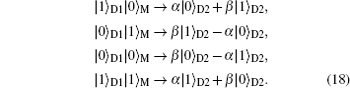
When the envolution time satisfies the condition λt = π/2, we can get the state
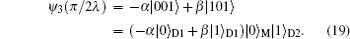
The above result shows that the information encoded in the electron state of one QD1 returns back to its original place. When the coefficients’ values are set as
α = 1,
β = 0, the initial state is |100〉, the target state is |001〉, as is clearly seen from Eq. (
19). The transformation of the state from |100〉 to |001〉 exactly corresponding to the situation of the electron “
teleportationlike” transfer described in Ref. [
7]. Interestingly, when
α,
β are general coefficients, the state of the left dot is transformed from
Ψ3D(0) =
α|0〉 +
β|1〉 to
Ψ3D(
π/2
λ) = –
α|0〉 +
β|1〉. From the point of quantum information transmission, the left quantum dot keeps its initial information, only including a phase reversal.