Cite this Article
Xiong Qing-Yun, Shen Qi-Xia, Li Rui-Zi, Shen Jiang, Tian Fu-Yang. First-principle investigation on the thermodynamics of X2N2O (X = C, Si, Ge) compounds. Chinese Physics B, 2016, 25(2): 026501  
Permissions
First-principle investigation on the thermodynamics of X2N2O (X = C, Si, Ge) compounds
Xiong Qing-Yun1, Shen Qi-Xia2, Li Rui-Zi1, Shen Jiang1, Tian Fu-Yang1, †,
Institute for Applied Physics, University of Science and Technology Beijing, Beijing 100083, China
Department of Mathematics and Physics, Zhengzhou University of Science and Technology, Zhengzhou 450064, China

 

† Corresponding author. E-mail: tfy123@126.com

Project supported by the Fundamental Research Funds for the Central Universities, China (Grant No. FRF-TP-14-029Al).

Abstract
Abstract

The structures under different pressures, elastic properties, electronic structures and lattice vibrations of the X2N2O (X = C, Si, Ge) compounds are investigated by using the first-principle method. Based on the phonon density of state, the thermodynamic properties of the present compounds are studied under different pressures and at different temperatures. The structural parameters including the bond lengths and bond angles are in agreement with available experimental measurements and theoretical calculations. We employ the elastic theory to calculate the nine independent elastic constants (Ci j) and the derived elastic moduli (B, G, E, v). Results indicate that these X2N2O (X = C, Si, Ge) compounds are mechanically stable and show the brittle behaviors. The electronic properties of the present compounds are analyzed by using the band structure and density of states. The phonon dispersion calculations imply that the present compounds are dynamically stable. Based on the quasi-harmonic approximation, the calculations of the specific heat indicate that the temperature in a range of 0 K–1500 K and pressure in a range of 0 GPa–40 GPa have a large effect on the thermal quantities of Ge2N2O, compared with on those of the C2N2O and Si2N2O compounds.

PACS: 62.20.de;64.70.qd;74.20.Pq;
Keyword:ceramics;ab initio calculations;crystal structure;elastic properties;thermodynamic properties;
1. Introduction

Silicon oxynitride (Si2N2O) and germanium oxynitride (Ge2N2O) are widely used as the high-temperature structural materials and viewed as the promising functional materials.[1–3] Much attention has been paid to the superior physical and chemical properties, such as good thermal shock resistance, high mechanical strength and excellent oxidation resistance.[4–7] The hypothetical carbon oxynitride C2N2O has the same crystal structure as the Si2N2O and Ge2N2O compounds.[8,9] It was theoretically predicted that the mechanical properties of C2N2O are superior to Si2N2O and Ge2N2O.[3,10]

Most of theoretical and experimental reports focus on structural and mechanical properties of X2N2O (X = C, Si, Ge). For example, the electronic structures and chemical bondings of these compounds were studied by the orthogonalized linear combination of atomic orbitals (OLCAO) method[11] and the full-potential linear Muffin-tin orbitals (LMTO) method.[10] The results showed that C2N2O has stronger covalent bonding than Si2N2O and Ge2N2O. Ding[3] and Ding et al.[12] studied the hardness values of the X2N2O (X = C, Si, Ge) and found that the C2N2O may be the potential superhard material, whereas the hardness of Ge2N2O is the smallest in these three compounds. On the experimental side, extensive studies focused on the preparation and improving mechanical properties of Si2N2O ceramic.[4,7,13] Wu and Li[1,14] indicated the relationship between purity and Vickers hardness of Si2N2O with the final sintering temperature. More recently they successfully fabricated a nano-grained Si2N2O ceramic without second phases. Srinivasa and Cariz,[5] and Srinivasa et al.[15] determined the lattice parameters, bond properties of Si2N2O and Ge2N2O at pressure P = 2.3 and 2.54 GPa by the time-of-flight neutron diffraction. Haines and Santoro[16] found the complete amorphization of Si2N2O occurs above P = 41 GPa by the x-ray power diffraction and the infrared absorption. Although the electronic properties and thermodynamic properties of some ceramics were reported,[17–22] as a widely used refractory, however, few experimental and theoretical data about the thermodynamic properties of X2N2O (X = C, Si, Ge) compounds have been reported so far.

In the present work, we systematically investigate the structures under different pressures, elastic properties, and electronic structure of X2N2O (X = C, Si, Ge) using the first-principle calculations. The thermodynamic properties are calculated via quasi-harmonic approximations under different pressures (0 GPa–40 GPa) and at various temperatures (0 K–1500 K). The lattice parameters, average bond lengths and bond angles are presented in detail. The results of elastic constants and lattice vibration show that these compounds are mechanically and dynamically stable and the derived mechanical moduli are further studied. The band structures of these compounds are calculated and the contributions of different orbitals to density of state (DOS) are discussed. The specific heat Cv values are obtained at different temperatures (0 K–1500 K) and under different pressures (0 GPa–40 GPa).

The rest of the paper is organized as follows. In Section 2 we present the theoretical tool and give the important details of the numerical calculations. The results are presented and discussed in Section 3. And finally, we draw some conclusions from the present studies in Section 4.

2. Computational details
2.1. First-principle calculations

All first-principle calculations were carried out using Cambridge Series of Total Energy Package (CASTEP) code based on the density functional theory (DFT).[23] The effects of the exchange–correlation energy were described by the generalized gradient approximation (GGA) in the form of Predew–Burke–Ernzerhof (PBE) potential.[24] The optimization was performed until the forces on the atoms are less than 0.01 eV/Å and all the stress components were less than 0.05 GPa. Ultrasoft pseudo potentials were used. The electronic wave functions were expanded in a plane-wave basis set with a cutoff energy of 400 eV, and 8 × 13 × 13 Monkhorst–Pack meshes were employed for the Brillouin-zone k-point samplings. The self-consistent convergence of the total energy was 5.0 × 10−6 eV/atom. The finite displacement method was employed to calculate the phonon of state and the phonon dispersion via the constructed 3 × 3 × 3 supercell.

2.2. Elastic method

The stress-strain method was used to evaluate the elastic constants of the crystal structure. Owing to the crystal symmetry, the present compounds can be described by the nine independent elastic stiffness coefficients (C11, C22, C33, C44, C55, C66, C12, C13, and C23). For calculating the elastic constants, we used the volume-conserving strains. The maximum strain amplitude is set to be 0.003. The number of steps is 6 for each strain. The mechanical parameters such as bulk modulus (B), shear modulus (G), Young’s modulus (E), and Poisson’s ratio (v) can be calculated via Voigt–Reuss–Hill (VRH) approximation.[25] For the orthorhombic crystal, the Voigt bound of bulk modulus (BV) and the Voigt bound of shear modulus (GV) in Voigt approximation are calculated directly from elastic constants by

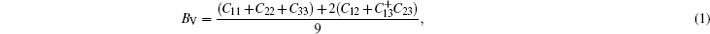
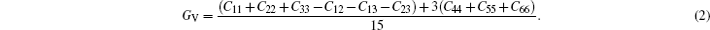
In Reuss approximation, the Reuss bound of bulk modulus (BR) and the Voigt bound of shear modulus (GR) are calculated by

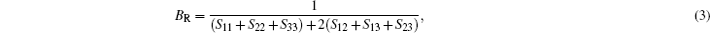
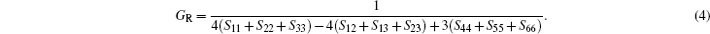
In the formulas above, the Si j are elastic compliance constants, which are the inverse matrix of Ci j. In Voigt–Reuss–Hill method, the bulk moduli B and shear moduli Gare calculated by arithmetic average of Voigt and Reuss bounds as follows:

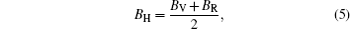
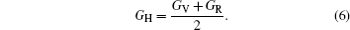
Then E and v can be calculated from the following equations:

2.3. Thermodynamic calculations

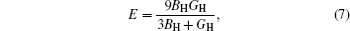
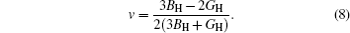
As is well known, the calculations of phonon spectra can be used to compute energy (E), entropy (S), free energy (F), and lattice specific heat (CV) each as a function of temperature via the quasi-harmonic approximation.[26] The temperature dependence of the energy can be expressed as

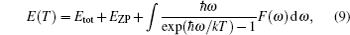
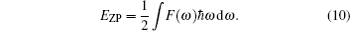
where Etot is the total energy and calculated at 0 K, k is the Boltzmann’s constant, ħ is the Planck’s constant, and F(w) is the phonon density of states. The zero point vibrational energy EZP is evaluated as

The vibrational contribution to the free energy F(T) is expressed as

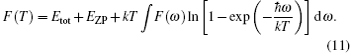
The lattice contribution to the specific heat Cv is written as

3. Results and discussion
3.1. Structural properties

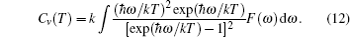
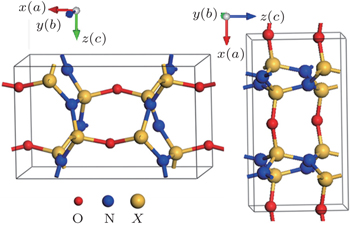
The X2N2O (X = C, Si, Ge) compounds are of the orthorhombic structure (shown in Fig. 1) with the space group symmetry Cmc21. The calculated structural parameters of X2N2O (X = C, Si, Ge) are listed in Table 1, along with the available data from experiments and other theoretical results. Although the structures of Ge2N2O and C2N2O are the same as that of Si2N2O, while Si atoms are replaced with Ge or C atoms,[5,10] their lattice parameters are very different. Owing to the larger covalent atomic radius of Ge, the lattice parameters of Ge2N2O are largest among three compounds (0.77 Å for C, 1.17 Å for Si, and 1.22 Å for Ge).

Fig. 1. Crystal structures of the orthorhombic- X2N2O (X = C, Si, Ge) compounds.
Table 1.

Comparisons among the calculated values of equilibrium lattice parameters (a, b, c) (Å), average bond length L (Å), and bond angle (°), the experimental data and other theoretical results. For each compound, the data in the first line are from the present calculations, the data in the second line are the results cited from the references, and the data in the third line refer to the experimental results.

.

For X2N2O (X = C, Si, Ge), one oxygen atom and three nitrogen atoms form a tetrahedron structure, and the X element is located in the center of the tetrahedron structure. With the increase of atomic radius of X atom (X = C, Si, Ge), the average X–N and X–O bond lengths increase, while the X–O average bond length is shorter than the X–N ones. Whereas the average bond angles of O–X–N and N–X–N are still 109°. As is well known, the sp3 hybrid in the carbon group results in the tetrahedron structure with a bond angle of 109°. The bond angle of X–O–X in Si2N2O is large, compared those of the C2N2O and Ge2N2O compounds. The N–X–N bond angle is about 120°for the three present compounds.

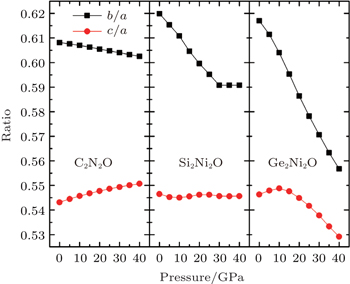
Considering the fact that the lattice parameters (a, b, c) of each compound are not equal to each other, we show in Fig. 2 the lattice parameter ratios each as a function of pressure P in a range of 0 GPa–40 GPa. For C2N2O, the b/a ratio linearly decreases (c/a linearly increases) with increasing pressure. The c/a ratio almost has no change, and b/a linearly decreases from P = 0 GPa to P = 30 GPa, then tends toward a constant between 30 GPa and 40 GPa for Si2N2O. With the increase of the pressure, the b/a ratio quickly decreases, whereas c/a slightly increases for P in a range of 0 GPa–10 GPa, then linearly decreases for Ge2N2O with the largest lattice parameters in the present compounds. The anisotropy mainly derives from the covalent bondings between X (C, Si or Ge), N and O atoms in the X2N2O compounds.

Comparative investigations of these structures are helpful to understand the effects of C and Ge on the elastic and thermodynamic properties in these compounds. The equilibrium structures under zero pressure are used for discussing the elastic properties, band structures, phonon information, and thermodynamic properties.

Fig. 2. Variations of lattice parameter ratio (b/a and c/a) of crystal structure with pressure for the orthorhombic- X2N2O (X = C, Si, Ge) compounds.
3.2. Elastic properties

Elastic constants (Cij) are significant parameters of solid materials, which provide important information about the mechanical stability, anisotropic feature, bonding characteristics, ductility, etc.[31] Listed in Table 2 are the nine independent elastic constants and bulk mechanical properties derived from them for the orthorhombic-X2N2O (X = C, Si, Ge) compounds. All elastic constants are larger than zero (Cij > 0), and they satisfy the known stability condition for orthorhombic crystal,[32] i.e., C11 + C22 − 2C12 > 0, C11 + C22 + C33 + 2(C12 + C13 + C23) > 0, C11 + C33 − 2C23 > 0, and C22 + C33 − 2C23 > 0. According to these criteria, results indicate that the orthorhombic structures of X2N2O (X = C, Si, Ge) are mechanically stable. Our calculations are well consistent with the theoretical results from different exchange-correlation approximations or interatomic potentials.[3,27,29,30] Compared with Si2N2O and Ge2N2O, C2N2O has the mechanical strength predicted by the large elastic constants and bulk modulus B, which may derive from the strong sp3 hybridization of C2N2O. It is notable that the present elastic constants are calculated under P = 0 and at T = 0 K.

The calculated values of shear modulus G, Young’s modulus E, and Poisson’s ratio ν are listed in Table 2, and the experimental data and other theoretical results are also given there. For C2N2O, our calculated values of B, G, and E are all a little smaller than the available theoretical calculations, whereas for Ge2N2O our calculations are slightly larger than the previously theoretical results. In the case of Si2N2O, our calculated G value is 96.6 GPa and E value is 238.2 GPa, which are in excellent agreement with the recent experimental values of 93.1 GPa and 223.6 GPa respectively. The Poisson ratio v values of three compounds are also reasonable compared with the recent theoretical values.[3,27,29] Generally speaking, the material behavior is in a ductile manner when B/G > 1.75, otherwise in a brittle manner.[33] The B/G ratio values of C2N2O, Si2N2O, and Ge2N2O are 1.028, 1.540, and 1.328, respectively. It is indicated that X2N2O (X = C, Si, Ge) compounds are very brittle. The Poisson’s ratio v is often used to study the ductility or brittleness in metallic alloy. A material is ductile when v > 0.33.[34] The alloy with large B/G often has a large Poisson’s ratio v. In the three present compounds, C2N2O has a slightly smaller v of 0.133 whereas the two others have large and comparable v values.

Table 2.

Calculated elastic constants Cij (GPa) and elastic moduli (GPa) of the orthorhombic-X2N2O (X = C, Si, Ge) compounds.

.
3.3. Electronic structure

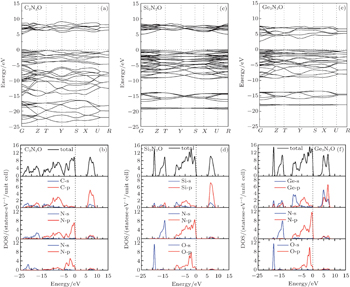
The calculated band structures and densities of state (DOSs) of X2N2O (X = C, Si, Ge) are shown in Fig. 3. The obtained band gap values are 5.18 eV (C2N2O), 5.00 eV (Si2N2O), and 2.76 eV (Ge2N2O), respectively. In order to further investigate the electronic structures, we present total densities of state and partial electron densities of states (PDOSs) for X2N2O (X = C, Si, Ge) in Figs. 3(b), 3(d), and 3(f). It is clear that there are three valence regions for each of these compounds. The lowest energy band (below −18 eV) for X2N2O (X = C, Si, Ge) is mainly composed of O-s orbitals. The DOS in the next energy band is dominated by N-s orbitals between −18 eV and −16 eV (−13 eV) for C2N2O (Si2N2O and Ge2N2O). The hybridization exits between X-p and N-s orbitals for X2N2O in this region. The N-p orbitals of these compounds dominate the density of state in the upper valence band region. For C2N2O the N-p and C-s orbitals hybridize between −15 eV and −12 eV and for Si2N2O (Ge2N2O) the N-p and Si (Ge)-s hybridize between −10 eV and −7 eV. Then the p orbitals of X, N, and O hybridize with each other near the Fermi level. C-p and Si-p dominate density of states of C2N2O and Si2N2O in the conduction band region. For Ge2N2O, the density of state is composed of Ge-s between 3 eV and 6 eV, and Ge-p orbitals dominate the density of state from 6 eV to 10 eV.

Figures 3(b), 3(d), and 3(f) separately show the typical sp hybridizations of X. The strong covalent bonding may result in the inherent brittle behaviors of the present compounds. The different values of band gap for X2N2O (X = C, Si, Ge) are mainly attributed to the X-s and p orbitals.

Fig. 3. Band structures and DOSs for X2N2O (X = C, Si, Ge).
3.4. Thermodynamic properties

Figure 4 shows the phonon DOS and the phonon dispersions along the high symmetry directions for X2N2O (X = C, Si, and Ge). The unit cell of X2N2O contains ten atoms, which gives rise to 30 phonon branches in total, of which acoustical branches are three and optical modes are 27. Owing to degeneracy the actual number is reduced along each different direction. No imaginary phonon frequency in the whole Brillouin zone suggests that the present compounds are dynamically stable in ambient condition, i.e., under no compression (shown in Fig. 4) and under compression (no shown). There is a gap in optical phonon mode between the Si2N2O and Ge2N2O compounds. The acoustic phonon modes have interactions with the partial low-lying optical phonon modes. The highest frequencies of three compounds are very close to 42 THz, 35 THz, and 30 THz, respectively, due to the influences of differences among atomic mass values.

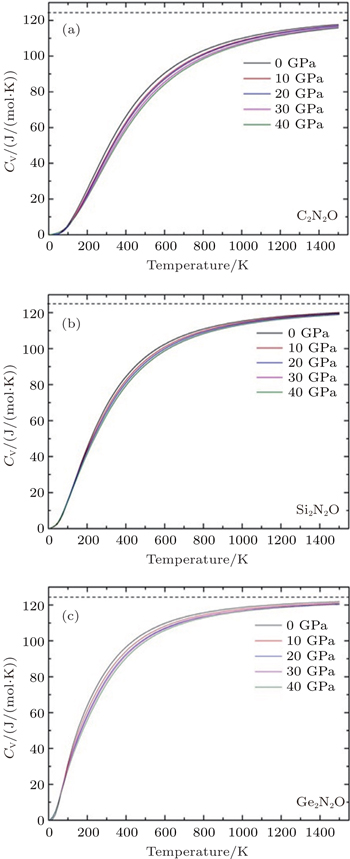
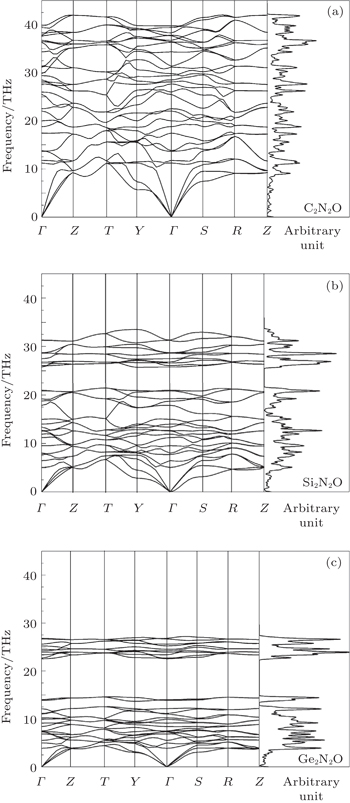The specific heat is a measure of how well the substance stores the heat. The calculated values of specific heat CV as a function of temperature for all the investigated compounds at different pressures are shown in Fig. 5. We can clearly see that at high temperatures the specific heat at constant volume obeys the Dulong Petit limit. At the intermediate temperatures, the temperature dependent specific heat is governed by the details of vibrations of the atoms. With increasing pressure, CV as a function of temperature slightly decreases. From Fig. 5 we observe that C2N2O has the lowest value of specific heat in all the compounds. The CV value of Ge2N2O increases more remarkably than those of Si2N2O and C2N2O with increasing temperature under a given pressure before it is close to the Dulong–Petit limit.

Fig. 4. Phonon dispersions and phonon DOSs for X2N2O [X = C, Si, Ge, corresponding to panels (a), (b), and (c)].
Fig. 5. Variations of Cv with temperature T at different pressures for X2N2O [X = C, Si, Ge, corresponding to panels (a), (b), and (c)].
4. Conclusions

In this work, the crystal structures, elastic properties, electronic structures and thermodynamic properties of X2N2O (X = C, Si, Ge) are investigated using the first-principle method. The orthorhombic structure is thermodynamically stable indicated by the calculations of the elastic constants and the lattice vibration. The obtained results of the structural parameters, elastic constants (Cij), and aggregate elastic moduli (B, G, E) are in agreement with the corresponding experimental and theoretical results. The lattice parameters each as a function of pressure imply the strong anisotropies of X2N2O. The different values of band gap for X2N2O (X = C, Si, Ge) are mainly attributed to the X-s and p orbitals. The specific heat CV values are calculated at different temperatures and under different pressures via the quasi-harmonic approximation. Compared with the cases of the Si2N2O and C2N2O compounds, the specific heat at constant volume of Ge2N2O remarkably increases with increasing temperature at given pressure before it is close to the Dulong–Petit limit.

Reference
1Wu S JLi X M 2012 Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 43 4859
2Tong Q FWang J YLi Z PZhou Y C2007J. Eur. Ceram. Soc.281227
3Ding Y 2012 Physica B 407 2190
4Ohoashi MTabata HKanzaki S 1991 J. Am. Ceram. Soc. 74 109
5Srinivasa S RCariz L1975J. Appl. Cryst.12511
6Wang SQYan Y H1998China Ceramics 3442
7Tong Q FWang J YLi Z PZhou Y C 2007 J. Eur. Ceram. Soc. 27 4767
8Takarabe KSougawa MKariyazaki HSueoka K 2012 J. Appl. Phys. 112 013537
9Jorgensen J DSrinivasa S R 1979 Acta Cryst. B 35 141
10Ivanovskii A LMedvedeva N IKontsevoi O YuShveikin G P 2000 Phys. Stat. Sol. 221 647
11Ching W Y 1981 Phys. Rev. B 24 5788
12Ding Y CChen MGao X YJiang M H 2012 Chin. Phys. B 21 067101
13Ohashi MNakamura KHirao KToriyama MKanzaki S 1997 Ceramics International 23 27
14Wu S JLi X M 2013 Int. Journal of Refractory Metals and Hard Materials 36 97
15Srinivasa SCartz LJorgensen J DWorlton T GBeyerlein RBilly M1977J. Appl. Cryst.10167
16Haines JSantoro M 2008 Phys. Rev. B 77 144206
17Song W BWang J QLi Z YLiu X SYuan B HLiang E J 2014 Chin. Phys. B 23 66501
18Wu M MPeng JZu YLiu R DHu Z BLiu Y TChen D F 2012 Chin. Phys. B 21 116102
19Yang Z JLi JLinghu R FCheng X LYang X D 2013 J. Alloys Compd. 574 573
20Yang Z JTang L. Guo A MCheng X LZhu Z HYang X D 2013 J. Appl. Phys. 114 083506
21Yang Z JLi JLinghu R FSong X SCheng X LZhu Z HYang X D2013Eur. Phys. J. B86
22Yuan B HYuan H LSong W BLiu X SCheng Y GChao M JLiang E J 2014 Chin. Phys. Lett. 31 076501
23Segall M DLindan P J DProbert M JPickard C JHasnip P JClark S JPayne M C 2002 J. Phys.: Condens. Matter 14 2717
24Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
25Hill R 1952 Proc. Phys. Soc. A 65 349
26Baroni Sde Gironcoli SCorso A D 2001 Rev. Mod. Phys 73 515
27Goumri-Said SKanoun-Bouayed NReshak A HKanoun M B 2012 Comput. Mater. Sci. 53 158
28Idrestedt IBrosset C 1964 Acta Chemica Scandinavica 18 1879
29Liu BWang J YLi F ZTong Q FZhou Y C 2009 J. Phys. Chem. Solids 70 982
30Boch PGlandus J C 1979 J. Mater. Sci. 14 379
31Yang Z JLi JLinghu R FCheng X LYang X D 2013 J. Alloys Compd. 551 435
32Xiao BFeng JZhou C TJiang Y HZhou R 2011 J. Appl. Phys. 109 023507
33Yan H YZhang M GHuang D HQun W 2013 Solid State Sci. 18 17
34Gu X JMcDermott A GPoon S JShiflet G J 2006 Appl. Phys. Lett. 88 211905