Cite this Article
Jiang Xiao-Xu, Chen Guan-Yu, Li Yu-Tong, Cheng Xin-Lu, Tang Cui-Ming. Phase transition and chemical decomposition of liquid carbon dioxide and nitrogen mixture under extreme conditions. Chinese Physics B, 2016, 25(2): 026102  
Permissions
Phase transition and chemical decomposition of liquid carbon dioxide and nitrogen mixture under extreme conditions
Jiang Xiao-Xu1, 2, Chen Guan-Yu1, 3, Li Yu-Tong2, Cheng Xin-Lu1, †, , Tang Cui-Ming4
Institution of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
Technology Development Center, Central Semiconductor Manufacturing Corporation, Wuxi 214000, China
Department of Physics and Mathematics, Sichuan University of Science and Engineering, Zigong 643000, China

 

† Corresponding author. E-mail: chengxl@scu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11374217, 11135012, and 11375262) and the Joint Fund of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. 11176020).

Abstract
Abstract

Thermodynamic and chemical properties of liquid carbon dioxide and nitrogen (CO2–N2) mixture under the conditions of extremely high densities and temperatures are studied by using quantum molecular dynamic (QMD) simulations based on density functional theory including dispersion corrections (DFT-D). We present equilibrium properties of liquid mixture for 112 separate density and temperature points, by selecting densities ranging from ρ = 1.80 g/cm3 to 3.40 g/cm3 and temperatures from T = 500 K to 8000 K. In the range of our study, the liquid CO2–N2 mixture undergoes a continuous transition from molecular to atomic fluid state and liquid polymerization inferred from pair correlation functions (PCFs) and the distribution of various molecular components. The insulator–metal transition is demonstrated by means of the electronic density of states (DOS).

PACS: 61.20.Ja;62.50.–p;71.15.Pd;
Keyword:liquid CO2–N2 mixture;quantum molecular dynamic (QMD) simulations;DFT-D;phase transition;
1. Introduction

With the continuing development of fluid science,[1] shock physics, detonation science,[2] and geophysics,[3] the study of material properties under extreme conditions[4] has attracted extensive attention. In the last decade, this has been made possible due to both the increasing accuracy of experimental diagnostics and the expanding computing capabilities. On the experimental techniques side, gas gun,[5] chemical explosives,[6] and pulsed power,[7,8] have been adopted in dynamic compressions, where pressures could reach the megabar region. Among the theoretical models, thermochemical calculations have been developed and concentrated mainly on the dynamic compressions of energetic materials[9] and the equation of state (EOS) of these detonation products, of which N2 and CO2 are usually the main components because of their relatively large negative formation enthalpies.[10] Thermochemical calculations are based on a microscopic description of pair interactions determinated by explosive detonation data.[11] Nevertheless, the EOS predictions would lose their accuracies due to modifications of thermodynamic conditions and chemical composition of the detonation product mixture. Therefore, a variety of direct simulation methods have been developed, such as the path-integral Monte Carlo[12,13] (PIMC) and density-functional theory (DFT) molecular dynamics (MD).[14–17] Up to now, quantum molecular dynamics (QMD)[18,19] has been particularly suited for the study of such chemical processes as ionization, recombination, dissociation, and association of the various atomic species present in the warm dense matter.[18] In spite of the fact that these theoretical simulations in some cases already provided explanatory and predictive results, however, some discrepancies were observed between the results of QMD calculations and the thermochemical predictions.[10,20] Some theoretical results agree well with experiment data only in the case of higher density. It could be argued that DFT would not accurately predict the thermodynamic properties of warm dense matter with some systematic errors due to the fact that dispersion interactions are not taken into account.[21] The van der Waals (vdW) interactions are expected to play a significant role in determining the mechanical properties of some materials. In the study of the thermophysical properties for liquid carbon monoxide and nitrogen (CO–N2) mixture under extreme conditions,[22] we tried to explore the effect of vdW forces on liquid–liquid phase transition in the shock-compressed process, and found that the vdW interaction has a negative contribution to the pressure and tends to reduce the overestimation of the equilibrium volume.

To the best of our knowledge, the pure molecular systems, for exaple, liquid, argon,[23] hydrogen,[24–26] oxygen,[27–31] nitrogen,[32–34] nitrogen oxide,[18,35] and carbon monoxide[18,36] have been intensively studied with a variety of experimental techniques and theoretical simulations. There are only a few first-principles calculations concerning EOS for the liquid mixtures. In the present work, we study thermodynamic properties and chemical decomposition of liquid carbon dioxide and nitrogen (CO2–N2) mixture by using quantum molecular dynamic simulations based on density functional theory including dispersion corrections (DFT-D).[37,38] The liquid nitrogen undergoes a dissociative phase transition above 30 GPa and 7000 K indicated by experiments[39,40] and theoretical calculations.[32,41] Furthermore, as density or temperature increases, metallization can occur through first-order transition accompanied by molecular nitrogen to liquid polymeric phase transition.[42–44] However, the metallization of a compressed liquid mixture remains an open question. Here we study the insulator–metal transition in the liquid mixture by means of the electronic density of states (DOS). The second question from which this work originates is linked to recent results from our QMD simulations on the liquid CO–N2.[22] The data for liquid carbon dioxide[45–48] under shock compressions suggested that shock-induced dissociation transition of CO2 occurred at pressure above 34 GPa and temperature 4500 K along the Hugoniot, while our previous studies show that the decomposition of N2 molecules in liquid CO–N2[22] mixture occurs at temperature T ≈ 3500 K and pressure P ≈ 20 GPa, much lower than those of pure liquid nitrogen.[32,33,39,49–52] Therefore, we will pay particular attention to the constituency of the dissociative phase transition of liquid CO2–N2 mixture.

2. Method

In the past few years, density functional molecular dynamics (DFT-MD)[24,53,54] has become the most commonly used method to treat fluid systems. Nevertheless, the accuracy of density functional theory (DFT) (Ref. [24]) has often been brought into question, because dispersion interactions are not taken into account.[21] In this study, in order to make up for the effect of dispersion on thermodynamics of the liquid mixture, which is absent in DFT simulations, Perdew–Burke–Ernzerhof augmented by a damped empirical correction for dispersion-like interactions (PBE-D)[55] is adopted. In our work, we employ the Gaussian and plane wave (GPW) method code QUICKSTEP as implemented in CP2K to calculate all of the molecular dynamics trajectories. This method describes the electronic structure by using the density functional theory (DFT) (Ref. [24]) with the generalized gradient approximation (GGA)[56] exchange–correlation functional combined with the Double Zeta Valence with Polarization (DZVP) basis set and the GTH-type pseudopotential.[57,58] Taking the effect of dispersion into consideration, all of the geometry optimizations of isolated molecules are performed with PBE-D. For the nitrogen molecule, the length of triple bond in the molecule is equal to 1.119 Å, comparable to the experimental value of 1.097 Å. For the carbon dioxide molecule, an interatomic distance of C–O of 1.160 Å is calculated in comparison with the experimental value of 1.162 Å, and the molecule is linear. For all these molecules, satisfactory agreement on the geometry of the isolated molecule is achieved, confirming the validity of the method of simulating the intramolecular interactions.

The calculations are performed by a series of volume-fixed unit cells, while keeping the number of molecules of each kind fixed. The supercell in our MD simulation contains 48 molecules (120 atoms) in the case of equimolar binary carbon dioxide and nitrogen (CO2–N2) mixture (24 CO2 and 24 N2 in the form of molecules). Periodic boundary conditions are used in the three directions. The tests of the effects of finite-size are performed with larger cells, each containing 64 molecules, corresponding to densities of 1.80 g/cm3 and 2.89 g/cm3 and a temperature of 2000 K. Compared with the case in our 48-molecule system, the changes in the pressure and internal energy are not significant and smaller than 2%.

We perform fixed-volume molecular dynamics simulations for 112 separate density and temperature points, with seven different specific densities from ρ = 1.80 g/cm3 to 3.40 g/cm3. For each density, the simulation is executed for a temperature range from T = 500 K to 8000 K, and the temperature is increased in steps of ΔT = 500 K. The initial configurations are obtained after a stabilization of the liquid at the same density and a lower temperature T = 300 K, ensuring that all the simulations are started at 1:1 carbon dioxide and nitrogen molecular (CO2–N2) mixture. In order to obtain accurate enough thermodynamic quantities, we let the dynamic simulations last 30 ps, including the system equilibration time for more than 10 ps and the time of calculated properties at least 10 ps, depending on different systems. Also, we obtain the EOS data (P, U, T) and pair correlation functions by averaging over the final 10-ps calculations for all the systems. As an example, the time evolutions of the temperature, the potential energy, and the pressure of the liquid CO2–N2 mixture at T = 2000 K and ρ = 2.20 g/cm3 are shown in Fig. 1.

Fig. 1. Time evolutions of the temperature, the potential energy, and the pressure of the liquid CO2–N2 mixture during the DFT-D NVT simulation at T = 2000 K and ρ = 2.20 g/cm3. The unit 1 hartree = 110.5 × 10−21 J.

All quantum molecular dynamics (QMD) calculations are performed within the canonical ensemble (the NVT ensemble) in integration time steps of 0.5 fs, which is applied to all degrees of freedom. The plane-wave energy cutoff radius of 500 Ry (1 Ry = 13.6056923(12) eV) is employed, which is sufficient to obtain a converged energy and force, and a Nosè–Hoover thermostat[59] is used to adjust the system temperature.

3. Result and discussion
3.1. Equation of state (EOS)

We present our QMD simulation results for equilibrium properties of liquid carbon dioxide and nitrogen (CO2–N2) mixture for 112 separate density and temperature points. In the region of our study, the CO2–N2 mixture system undergoes the molecular–atomic fluid state transition and liquid polymerization transition, coinciding with an insulator–metal transition. Thus, it is interesting to examine molecular dissociation and the insulator–metal transitions in studying the thermophysical properties of liquid CO2–N2 mixture under extreme conditions. To check on the accuracy of DFT-D calculations, isotherms at T = 2000 K and T = 3000 K are shown and compared with DFT results calculated by Jean–Bernard Maillet[10] in Fig. 2.

Fig. 2. Isotherms at T = 2000 K (squares) and T = 3000 K (circles) for liquid CO2–N2 mixture. Solid symbols correspond to DFT results (Ref. [10]), and empty symbols correspond to our DFT-D results.

The agreement between DFT-D results and DFT data is good over the whole density range for both isotherms. This is mainly because of the insignificant contribution of van der Waals interactions in those ranges of pressure and temperature. However, as the density and temperature increase, the molecules of the mixture are dissociated and DFT may lose the accurate predictions due to the lack of van der Waals interactions. A more detailed study of the phase transition can be acquired by isochores. The relations of pressure–temperature for different isochores derived from our DFT-D calculations are displayed in Fig. 3.

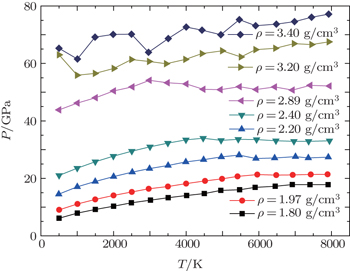Fig. 3. Pressure–temperature relations for liquid CO2–N2 mixture along various isochores derived from our QMD/DFT-D simulations.

As shown in Fig. 3, at the lowest density ρ = 1.80 g/cm3, the pressure increases monotonically with temperature increasing up to 7000 K. When the temperature continues to increase from 7000 K to 8000 K, the pressure does not keep increasing, but remains the same. This indicates that as the temperature increases up to 7000 K, the liquid mixture begins to dissociate, so that the drop in the pressure is not compensated for by the increase of the kinetic during this transition.

At a higher density ρ = 1.97 g/cm3, when the temperature increases up to 6000 K, (ΔP/ΔT)V is slightly negative, which indicates strongly that the mixture is undergoing a phase transition. Remarkably, with the increase of the density, the phase transition takes place at lower temperature, leading to a region of (ΔP/ΔT)V < 0. For example, at a density of 2.40 g/cm3, (ΔP/ΔT)V < 0 is present at a temperature about of 4500 K, while the first drop of the pressure occurs only at 3000 K, when the density increases up to 2.89 g/cm3. At sufficiently high densities of ρ = 3.20 g/cm3 and 3.40 g/cm3, the pressure–temperature (P–T) plane curves each have more than one fold point. This could possibly be caused by a series of continuous phase transitions, such as the dissociations of CO2 and N2 molecules, the recombinations of C, N, and O atoms, the formations of large clusters, and the associations of products under extreme conditions of high pressure and temperature.

As an example, according to the analysis of the P–T curve, at the density of 2.40 g/cm3, the first phase transition of liquid CO2–N2 mixture takes place at a temperature of about 4500 K and pressure up to 34 GPa, which agrees with the conditions of shock-induced dissociation for liquid CO2 reported by Nellis et al.[45] So, it suggests that this phase transition is caused by the decomposition of CO2 molecules. It is not difficult to find that N2 molecules do not dissociate at much lower temperature and pressure (T ≈ 4000 K and P ≈ 20 GPa) than those of molecular nitrogen inferred from experiment[39,49] and predicted in theory[32,33,50–52] (T ≈ 7000 K and P ≈ 31 GPa), as we have mentioned in studying liquid CO–N2 mixture[22] under extreme conditions.

3.2. Constituency analysis

The pair correlation function (PCF)[27,36]

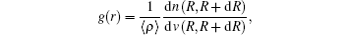
which represents the probability of finding an atom at distance r from a reference atom, and the distribution of various molecular components are two important quantities to characterize the evolution of the structure for the liquid mixture. Now, we employ these techniques to analyze the chemical processes of liquid CO2–N2 mixture under extreme conditions of temperature and pressure.

Firstly, we use VMD[60] to analyze the MD trajectories. The dependences of pair-correlation functions g(r)CO, g(r)NO, and g(r)NN, and the associated numbers of neighbors n(r)CO, n(r)NO, n(r)NN for liquid CO2–N2 mixture on temperature at the density of ρ = 2.40 g/cm3 are shown in Fig. 4. As seen in Fig. 4(a), when the temperatures are less than 4000 K, the first peak of g(r)CO is located at a distance of 1.17 Å (r = 1.17 Å), corresponding to the equilibrium bond length of C–O in the CO2 molecule (r = 1.162 Å), and it is slightly larger than the bond distance of the CO molecule (r = 1.128 Å). A more precise structural evolution of the CO2 molecules in the mixture with the number of oxygen neighbors of carbon atom n(r)CO are shown in Fig. 4(b). At the lower temperatures (T < 4000 K), a carbon atom has on average two oxygen atoms neighbors at a distance of 1.60 Å, indicating that the fluid CO2 has not yet begun to dissociate and no CO is formed. With the increase of temperature, the peak of the pair-correlation function g(r)CO reduces gradually in amplitude. At the higher temperatures (T > 4000 K), the peaks turn broader and move rightwards slightly and n(r)CO gradually decreases with temperature increasing. This tendency reveals that carbon dioxide molecules begin to dissociate at temperatures above 4000 K, and the corresponding pressure of about 34 GPa. To analyze the pair-correlation function g(r)NN and the associated number of neighbors n(r)NN shown in Figs. 4(e) and 4(f), the same methods are used. Figure 4(e) shows that the peak of g(r)NN corresponds to an equilibrium bond length of 1.12 Å, which is consistent with our result of geometry optimization of the nitrogen molecule. Moreover, in Fig. 4(f), the number of neighbors is equal to one at T < 4000 K, (which is the expected signal of the N2 molecule), and reduces to eighty percent for the higher temperature of 5000 K at a distance of 1.40 Å. It is not difficult to conclude that the dissociation of N2 molecules also begins at temperatures above 4000 K and pressure 34 GPa.

Fig. 4. Pair-correlation functions g(r)CO, g(r)NO, and g(r)NN, and the associated numbers of neighbors n(r)CO, n(r)NO, n(r)NN for liquid CO2–N2 mixture at a density of ρ = 2.40 g/cm3 for different temperatures.

Now we turn our attention to the formation of nitrogen oxides. Figures 4(c) and 4(d) show the evolutions of the covalent bond length between the nitrogen and the oxygen for eight different temperatures. At the lower temperatures (T < 4000 K), the PCFs (Fig. 4(c)) between nitrogen atoms and oxygen atoms stay at zero within the range of r = 1.60 Å, indicating that no nitrogen oxides are produced, and correspond to Fig. 4(d), which shows that a nitrogen atom has no oxygen atom neighbor at a distance of 1.60 Å, indirectly suggesting that the mixture has not been dissociated. When the temperature increases up to 5000 K, a sharp peak is seen in the g(r)NO centered near r = 1.16 Å, which is very close to the N–O bond length of NO (r = 1.15 Å), and slightly smaller than that of the NO2 molecule (r = 1.20 Å). We consider that this could be directly related to the formation of NO. With the continuous increase of temperature, the amplitude of the peak increases, suggesting that the nitrogen oxides increase with the decomposition of mixture.

Figure 5 shows the pair-correlation functions g(r)CO, g(r)NO, and g(r)NN, and the associated numbers of neighbors n(r)CO, n(r)NO, n(r)NN of liquid CO2–N2 mixture at the temperature of T = 3000 K for six different densities. At the lower densities (ρ ≤ 2.40 g/cm3), the first peak of g(r)CO shown in Fig. 5(a) corresponds to an equilibrium bond length of the CO2 molecule and n(r)CO displayed in Fig. 5(b) is equal to two, which is a character of the CO2 molecule. However, as the density increases up to 2.89 g/cm3, n(r)CO is more than two at a distance of 1.60 Å, suggesting that the carbon dioxide molecules are already dissociated, and the C–O cluster structures are produced. It is consistent with the point of (ΔP/ΔT)V < 0 in Fig. 3. However, from Figs. 5(c) and 5(d), we can know that N2 molecules begin to dissociate until the density increases up to 3.20 g/cm3 and NO is formed at the same time. Here, we do not give the pair-correlation functions g(r)OO nor the associated number of neighbors n(r)OO, because there are very few O–O bonds in a liquid mixture under any condition.

Fig. 5. Pair-correlation functions g(r)CO, g(r)NO, and g(r)NN, and the associated number of neighbors n(r)CO, n(r)NO, n(r)NN for liquid CO2–N2 mixture at the temperature of T = 3000 K for increasing densities.

In order to give more direct evidence of structural evolution, we analyze the MD trajectories by using the FINDMOLE code,[61] which can find molecule structures and count the number of molecules in MD simulations trajectories. The time evolutions of initial carbon dioxide and nitrogen, and several important products (dimer N2–CO2, NO, NO2, and N2O) in the liquid mixture are shown in Fig. 6.

Fig. 6. Comparisons of time evolutions of nitrogen (black lines) and carbon dioxide (red lines) mixture, and several important products [dimer N2–CO2 (blue), NO (dark cyan), NO2 (magenta), and N2O (dark yellow)] between the densities of ρ = 2.40 g/cm3 and ρ = 3.40 g/cm3 at three different temperatures of 1000 K, 4000 K, 6000 K, respectively. Populations are given per initial mixture molecule.

Figure 6 shows the comparisons of the populations of liquid mixture between the densities ρ = 2.40 g/cm3 and ρ = 3.20 g/cm3 at three different temperatures 1000 K, 4000 K, 6000 K. As seen from Fig. 6, at ρ = 2.40 g/cm3, carbon dioxide and nitrogen molecules begin to dissociate at the temperature above 4000 K, and the main product of nitrogen oxides is NO. However, at ρ = 3.20 g/cm3, the dissociation of CO2 molecules is quite obvious only at the temperature of 1000 K. All of these are consistent with the results from Figs. 3–5. We recall here that the initial configuration is composed of molecules 24CO2 and 24N2 only and that the DFT-D simulations are not performed from a pre-dissociated state. We find that the population curves of CO2 and N2 molecules overlap at the beginning of the period, suggesting that they dissociate almost concurrently. In particular, we also find essentially neither NO nor NO2 molecules occurs at ρ = 2.40 g/cm3, T = 2000 K and ρ = 3.20 g/cm3, T = 1000 K, but some intermediate N2O and stable dimer N2–CO2 are formed. The formation of NO (the main product) occurs after a large number of N2 molecules has decomposed. The decomposition rates of CO2 and N2 molecules and the final population of products are sensitive to both density and temperature. There is an increase of the liquid mixture decomposition rate with the increase of temperature at any density, because the probability to overcome the energy barrier is higher at elevated temperatures as mentioned by Rom et al.[62] As expected, the reaction rate also increases with compression due to the decomposition dynamics dominated by intermolecular interactions.[62] Besides the small molecules mentioned above, at the higher density and temperature, we find the highly transient large clusters of carbon–nitrogen–oxygen, and they contain above 40% of the total carbon and nitrogen of the system.

3.3. Density of states (DOS)

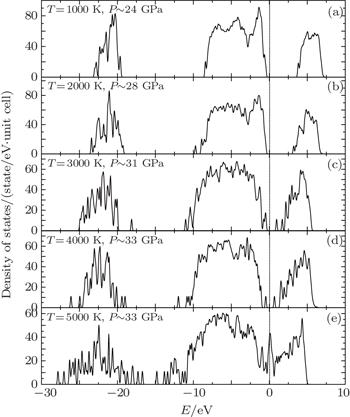
Among the regions of our study, the mixture system undergoes a continuous transformation, accompanied by an insulator–metal transition which is inferred from the electronic density of states (DOS) shown in Figs. 7 and 8.

Fig. 7. Electronic density of states of liquid CO2–N2 mixture at the density of ρ = 2.40 g/cm3, and corresponding temperatures of (a) 1000, (b) 2000, (c) 3000, (d) 4000, and (e) 5000 K, respectively. The Fermi energy EF is set to be zero (dotted line).
Fig. 8. Electronic density of states of liquid CO2–N2 mixture at the temperature of T = 3000 K and the densities of (a) 1.80, (b) 2.40, (c) 2.89, and (d) 3.40 g/cm3 respectively. The Fermi energy EF is set to be zero (dotted line).

All of the DOS calculations are performed with the GGA/PBE method[56] and the plane-wave cutoff at 500 eV. Figure 7 shows the electronic densities of states of liquid CO2–N2 mixture at the density of ρ = 2.40 g/cm3 and five different temperatures (1000–5000 K), respectively. The band gap of the liquid mixture changes from 3.5 eV at T = 1000 K, P∼ 24 GPa (Fig. 7(a)) to 1 eV at T = 3000 K, P∼ 31 GPa (Fig. 7(c)). When the temperature continues to increase up to 5000 K, which corresponds to the condition of liquid CO2–N2 mixture beginning to dissociate, the band gap finally closes (Fig. 7(e)), indicating that this mixture has completed the transition from insulator to metal. To discuss the role of the pressure in DOS, we also calculate the electronic densities of states of liquid mixture at the temperature of T = 3000 K and four different densities (1.80, 2.40, 2.89, and 3.40 g/cm3) shown in Fig. 8. At 31 GPa, the appearing of defect-like states in the middle of the electronic gap may arise from the formations of dimer chains and rings (as displayed in Fig. 9(a)).

Fig. 9. Instantaneous configurations of the system at densities of (a) 2.40 g/cm3 and (b) 3.40 g/cm3, respectively, and the corresponding temperatures are both 3000 K during simulations.

Figures 9(a) and 9(b) are instantaneous configurations of the system at 2.40 g/cm3, 3000 K and 3.40 g/cm3, 3000 K respectively, and corresponding to the states of Figs. 8(b) and 8(d). As density is further increased, the liquid mixture gradually loses its molecular character with increasing the number of polymeric chains (as shown in Fig. 9(b)), and eventually metallization occurs (over 64 GPa).

4. Conclusions

In this work, we study the thermodynamic properties and chemical decomposition of liquid carbon dioxide and nitrogen (CO2–N2) mixture under the conditions of extremely high densities and temperatures by using the quantum molecular dynamic simulations based on density functional theory including dispersion corrections (DFT-D). The selected pressures range from 6 GPa to 77 GPa, In this range, the liquid CO2–N2 mixture undergoes a continuous transition from molecular to atomic fluid state and liquid polymerization, accompanied by an insulator–metal transition. The liquid mixture molecules begin to dissociate at the temperature above 4000 K, and the corresponding pressure of about 34 GPa, which agrees with the conditions of shock-induced dissociation for liquid CO2. It suggests that the dissociation of N2 molecules do not occur under the N2 decomposition condition in liquid CO–N2 mixture. The main product of nitrogen oxides is NO, which has been testified. Other important products, such as stable dimer N2–CO2, few NO2, intermediate N2O, and the highly transient large clusters of carbon–nitrogen–oxygen are observed.

Reference
1Kortbeek P JSeldam C A TSchouten J A 1990 Mol. Phys. 69 1001
2Jones H DZerilli F J 1991 J. Appl. Phys. 69 3893
3Duan ZMoller NWeare J H 1996 Geochim. Cosmochim. Acta 60 1209
4Zhang Q LZhang PSong H FLiu H F 2008 Chin. Phys. B 17 1341
5Nellis W JRee F Hvan Thiel MMitchell A C 1981 J. Chem. Phys. 75 3055
6Mintsev V BFortov V E 2006 J. Phys. A: Math. Gen. 39 4319
7Knudson M DHanson D LBailey J EHall C AAsay J R 2003 Phys. Rev. Lett. 90 035505
8Bocharova I AAlnaser A SThumm UNiederhausen TRay DCocke C LLitvinyuk I V 2011 Phys. Rev. A 83 013417
9Guo FZhang HHu H QCheng X L 2014 Chin. Phys. B 23 046501
10Maillet J BBourasseau E 2009 J. Chem. Phys. 131 084107
11Zhao Y HLiu H FZhang Q L2012Acta Phys. Sin. 61230509(in Chinese)
12Magro W RCeperley D MPierleoni CBernu B 1996 Phys. Rev. Lett. 76 1240
13Pierleoni CCeperley D MBernu BMagro W R 1994 Phys. Rev. Lett. 73 2145
14Hohl DNatoli VCeperley D MMartin R M 1993 Phys. Rev. Lett. 71 541
15Kohanoff JHansen J P1995Phys. Rev. E54768
16Collins LKwon IKress JTroullier NLynch D 1995 Phys. Rev. E 52 6202
17Kwon IKress J DCollins L A 1994 Phys. Rev. B 50 9118
18Kress J DMazevet SCollins L ABlottiau P2004AIP Conf. Proc.70628910.1063/1.1780237
19Holst BRedmer RDesjarlais M P 2008 Phys. Rev. B 77 184201
20Maillet J BBourasseau EJomard G 2011 Chem. Phys. Lett. 507 84
21Byrd E F CRice B M 2007 J. Phys. Chem. C 111 2787
22Chen G YJiang X XCheng X LZhang H 2012 J. Chem. Phys. 137 054504
23Wang F HYang C LLi X JJing F Q2000Acta Phys. Sin.49114(in Chinese)
24Lenosky T JBickham S RKress J DCollins L A 2000 Phys. Rev. B 61 1
25Nellis W JMitchell A Cvan Thiel MDevine G JTrainor R J 1983 J. Chem. Phys. 79 1480
26Knudson M DHanson D LBailey J EHall C AAsay J RDeeney C 2004 Phys. Rev. B 69 144209
27Kress J DMazevet SCollins L A2002AIP Conf. Proc.6209110.1063/1.1483490
28Nellis W JMitchell A C 1980 J. Chem. Phys. 73 6137
29Hamilton D CNellis W JMitchell A CRee F Hvan Thiel M 1988 J. Chem. Phys. 88 5042
30Bastea MMitchell CNellis W J 2001 Phys. Rev. Lett. 86 3108
31Edwards P PHensel F2002Chem. Phys. Chem.353
32Kress J DMazevet SCollins L AWood W W 2000 Phys. Rev. B 63 024203
33Mailhiot CYang L HMcMahan A K 1992 Phys. Rev. B 46 14419
34Goncharov A FGregoryanz EMao H kLiu Z XHemley R J 2000 Phys. Rev. Lett. 85 1262
35Mazevet SBlottiau PKress J DCollins L A 2004 Phys. Rev. B 69 224207
36Zhang Y JWang CLi D FZhang P 2011 J. Chem. Phys. 135 064501
37Grimme S 2004 J. Comput. Chem. 25 1463
38Grimme S 2006 J. Comput. Chem. 27 1787
39Nellis W JRadousky H BHamilton D CMitchell A CHolmes N CChristianson K Bvan Thiel M 1991 J. Chem. Phys. 94 2244
40Nellis W JHolmes N CMitchell A Cvan Thiel M 1984 Phys. Rev. Lett. 53 1661
41Mazevet SJohnson J DKress J DCollins L A 2001 Phys. Rev. B 65 014204
42Mukherjee G DBoehler R 2007 Phys. Rev. Lett. 99 225701
43Boates BBonev S A 2009 Phys. Rev. Lett. 102 015701
44Donadio DSpanu LDuchemin IGygi FGalli G 2010 Phys. Rev. B 82 020102(R)
45Nellis W JMitchell A CRee F HRoss MHolmes N CTrainor R JErskine D J 1991 J. Chem. Phys. 95 5268
46Wang CZhang P 2010 J. Chem. Phys. 133 134503
47Boates BHamel SSchwegler EBonev S A 2011 J. Chem. Phys. 134 064504
48Root SCochrane K RCarpenter J HMattsson T R 2013 Phys. Rev. B 87 224102
49Hamilton D CRee F H 1989 J. Chem. Phys. 90 4972
50Martin R MNeeds R J 1986 Phys. Rev. B 34 5082
51Lewis S PCohen M L 1992 Phys. Rev. B 46 11117
52Alemany M M GMartins J L 2003 Phys. Rev. B 68 024110
53Galli GHood RHazi AGygi F 2000 Phys. Rev. B 61 909
54Bagnier SBlottiau PClerouin J2001Phys. Rev. E63015301
55Peverati RBaldridge K K 2008 J. Chem. Theory Comput. 4 2030
56Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
57Goedecker STeter MHutter J 1996 Phys. Rev. B 54 1703
58Hartwigsen CGoedecker SHutter J 1998 Phys. Rev. B 58 3641
59Nosé S 1984 J. Chem. Phys. 81 511
60Humphrey WDalke ASchulten K 1996 J. Mol. Graphics 14 33
61Guo FCheng XZhang H 2012 Combust. Sci. Technol. 184 1233
62Rom NHirshberg BZeiri YFurman DZybin S VGoddard III W AKosloff R 2013 J. Phys. Chem. C 117 21043