Cite this Article
Hu Bo, Shi Jie, Shi Sheng-Guo, Sun Yu, Zhu Zhong-Rui. Underwater asymmetric acoustic transmission structure using the medium with gradient change of impedance. Chinese Physics B, 2016, 25(2): 024305  
Permissions
Underwater asymmetric acoustic transmission structure using the medium with gradient change of impedance
Hu Bo1, 2, Shi Jie1, 2, †, , Shi Sheng-Guo1, 2, Sun Yu1, 2, Zhu Zhong-Rui1, 2
College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
Science and Technology on Underwater Acoustic Laboratory, Harbin Engineering University, Harbin 150001, China

 

† Corresponding author. E-mail: shijie@hrbeu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11204049 and 11204050), the Program for Changjiang Scholars and Innovative Research Team in University of Ministry of Education of China (Grant No. IRT1228), and the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant Nos. 20122304120023 and 20122304120011).

Abstract
Abstract

We propose an underwater asymmetric acoustic transmission structure comprised of two media each with a gradient change of acoustic impedance. By gradually increasing the acoustic impedances of the media, the propagating direction of the acoustic wave can be continuously bent, resulting in allowing the acoustic wave to pass through along the positive direction and blocking acoustic waves from the negative one. The main advantages of this structure are that the asymmetric transmission effect of this structure can be realized and enhanced more easily in water. We investigate both numerically and experimentally the asymmetric transmission effect. The experimental results show that a highly efficient asymmetric acoustic transmission can be yielded within a remarkable broadband frequency range, which agrees well with the numerical prediction. It is of potential practical significance for various underwater applications such as reducing vibration and noise.

PACS: 43.30.+m;43.30.Bp;43.30.Ky;
Keyword:asymmetric transmission;impedance;gradient;
1. Introduction

The electrical diode, the first man-made device enabling a rectifying current flux, has eventually led to substantial worldwide revolution. Many considerable efforts have been made to rectify other kinds of energy fluxes in a similar manner.[1–4] Li and Wang[3] presented the fundamental model of a thermal diode that has a rectifier effect on thermal energy. The thermal rectifying effects as well as the rectifying effects of solitary waves have been identified both theoretically and experimentally.[4] Recently, Liang et al. have numerically demonstrated a theoretical model of an acoustic diode and presented the first experimental demonstration of a rectified energy flux of acoustic waves by coupling a superlattice with a strong nonlinear medium.[5–7] It is noteworthy, however, that this working mechanism of nonlinear medium unavoidably leads to the problem of inefficient and unstable conversion acoustic energy conversion. Considering this problem in nonlinear media, many efficient linear structures have been proposed to transfer acoustic waves in the one-way direction.[8–11] Zhu et al.[8] have investigated theoretically the broadband structure of one-dimensional phononic crystal (PC) plates which present Lamb wave one-way mode transmission in certain frequency bands. Yuan et al.[9] have designed a two-dimensional model of a broadband directional acoustic waveguide with a linear PC to yield direction-dependent transmission properties for incident waves. Li et al.[10] have proposed a scheme of realizing broadband asymmetric acoustic transmission by utilizing PC-based materials with a gradient sound speed distribution. Additionally, inspired by the phenomenon that the propagating direction of acoustic waves can be continuously bent to follow a sinusoidal trajectory in the gradient-index PC, some studies have demonstrated the acoustic mirage or acoustic beam aperture modifier by using a gradient-index PC structure.[12,13] In practice, however, it is difficult for most of the underwater acoustic systems to use PC because of the restriction on water pressure and dimension, which means that these models cannot be applied to underwater engineering application. Therefore, it is necessary to explore the possibility of underwater asymmetric acoustic transmission structures which use other gradient-index acoustic materials.

In this work, we build a one-dimensional model of an underwater asymmetric acoustic transmission by utilizing the media each with a gradient change of impedance. It shows that asymmetric acoustic transmission can be achieved in a broadband frequency range. The design of the model is detailed in Section 2. Some numerical simulations are carried out and the typical results are obtained in Section 3. The media each with a gradient change of impedance is obtained by the precipitation method, and the performance of the proposed structure is verified experimentally in Section 4. A summary and discussion is given in Section 5.

2. Model

Consider a model, composed of three parallel regions, as shown in Fig. 1(a). Regions I and III are semi-infinite regions with the acoustic impedance Z0. Region II is composed of two media that are designed to have similar gradient profiles but with different fashions. In a previous study, one only attained the gradient profile of the model by means of changing sound speed but did not consider the problem of acoustic impedance mismatching to its surrounding medium. From an underwater practical acoustic standpoint, however, we believe that the best method is to gradually tune the specific acoustic impedance and sound speed, resulting in making sure of impedance-matching at the boundary. Thus, the media each with a gradient change of acoustic impedance are introduced, which is characterized by a smoothly and monotonically increasing acoustic impedance and sound speed with the increase of medium thickness.

(a) Schematic illustration of the model of underwater asymmetric acoustic transmission by utilizing the media each with a gradient change of impedance. The contrasty color denotes the distribution of specific acoustic impedance. The rigid (absorptive) boundary is denoted by gray (red) color. (b) The sketch map of the transmission of an acoustic wave incident from positive direction (gray arrow) and negative direction (blue arrow).

The rectangle ABCD is the first medium with acoustic impedance Z varying from Z0 to Zmax in the x direction, such that Z(xA) = Z0 and Z(xD) = Zmax (Zmax > Z0), i.e., there are the matched impedance and no step changes in the impedance at the boundary. Zmax is the acoustic impedance of the medium at surface CD. There is no variation of specific acoustic property in the y direction. On the other hand, the trapezia CDEF is the second medium with acoustic impedance varying from Zmax to Z0 along the positive x axis. The angle θ is the angle between EF and negative direction of y direction. The boundary BF and AD are chosen and made of rigid materials, and the boundary DE is assumed to be an ideal absorptive boundary. A plane wave is horizontally incident along the x axis, initiated in region I or region III. We generally define the propagating direction of acoustic wave incident from region I as the positive direction and incident from region III as the negative one.

The basic mechanism of asymmetric acoustic transmission in this model is briefly addressed here. As is well known, when the sound speed mismatch exists between two different media, an oblique incidence acoustic wave is refracted at the interface. The amount of wave beam bending is dependent on the sound speed difference according to Snell’s law. When a plane wave is incident from the positive direction, owing to the continuous distribution of acoustic impedance inside region II and the matched impedance with water at the boundary, the acoustic wave does not backscatter and can propagate along a straight line through region II. Although the angle θ leads to the impedance difference between the second medium and region III at the interface of EF because of the gradient profile only changing along the x axis, the trajectory of output acoustic wave is almost not bent due to the small angle θ. It means that the acoustic waves can pass through the model along the positive direction. On the other hand, when the acoustic wave is incident from the negative direction, the acoustic impedance of the second medium increases along the negative x axis. Therefore, at any interface parallel to CD, the refraction angle is always larger than the incidence angle. Thus, the propagating trajectory of the acoustic wave in the second medium can be continuously bent approximately parallelly to CD. Finally, all of the acoustic waves from the negative direction will reach the boundary DE, resulting in being absorbed by the absorptive boundary (see Fig. 1(b)). It is obvious that, by employing the medium with gradient change of impedance, the asymmetric behavior can be achieved in a simple model.

Our design is derived by employing the theory of geometric acoustics, which is a better understanding of how to change the trajectory of acoustic wave in this model. By calculating the sound speed contribution in the medium, one can readily predict the direction of refraction using Snell’s law.[14] Meanwhile, the ray-acoustic theory is helpful in predicting the position of acoustic ray. The acoustic ray equation is given by[15]

where c0 is the sound speed of water, θ0 is the initial incidence angle which is equal to the angle θ, θi, and gi are the refraction angle and the sound speed gradient of the i-th layer, respectively. In Eq. (1), the discrete lines are used to replace the continuous curve of the acoustic ray trajectory. Therefore, it is required that the discrete points N should be large enough to ensure that the difference between adjacent layers is very little and the acoustic impedance of each layer is the constant. Only by doing so can we describe the true acoustic wave trajectory. The acoustic characteristic of the medium with gradient change of impedance can be conveniently solved by using a transfer-matrix method as described in Ref. [16]. The transmission matrix Mi of the i-th layer is

where α = [∂ Z(x)/∂ x]/2Z(x) represents the relative change of acoustic impedance of the medium, Δx is the sampling space in x axis, k* = (k2 − α 2)1/2, k being the acoustic wave number. Therefore, we obtain the total transmission matrix M

where R and T refer to the sound reflection coefficient and transmission coefficient, respectively.

3. Numerical results and discussion

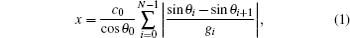
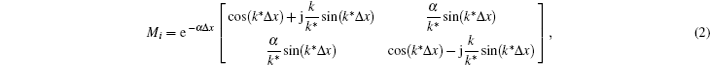
To examine the performance of the model described in the preceding section, a simulation study has been carried out. In the numerical simulation, boundary AD and CF are both set to be 0.1 m, the length of boundary CD is 0.05 m, and θ = 30°. Regions I and III are homogeneous water with mass density ρ0 = 1500 kg/m3, and sound speed c0 = 1000 m/s. Considering the realization of the medium with a gradient change of impedance in practice, the acoustic impedances and the sound speeds of two media are chosen as

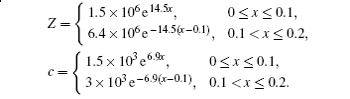
We first study the acoustic ray trajectories along the two sides of the model. It is noticeable that the medium in the trapezium CDEF plays a chief role in changing the direction of the incident wave. Thus, figure 2 shows the typical results of wave trajectories in the trapezium CDEF, which can help one visualize the wave formation. It is obvious that within the ray-acoustic, the designed structure allows the acoustic transmission along the positive direction but gradually changes the propagating direction of the acoustic ray from negative incidence toward the boundary DE as predicted. Moreover, there is no acoustic ray that can finally reach the boundary CD incident. The incident acoustic waves are completely absorbed by the absorptive boundary. This means that the acoustic transmissions along two directions exhibit remarkable asymmetric behavior.

Acoustic ray trajectories along the positive direction and the negative one.

Figure 3(a) shows the calculated transmissions of acoustic waves when the plane waves are incident from the two sides of the proposed structure within frequency band ranging from 100 Hz to 100 kHz. The solid line and the dashed line refer to the transmissions of acoustic waves from the positive and negative directions, respectively. It is apparent that with an increase in frequency, two transmission coefficients of the media decrease from 1 to 0. Furthermore, it is clearly observed that the significant difference between two curves also gradually increases in a frequency range from 2 kHz to 100 kHz, which is denoted by using the blue region in Fig. 3. The transmission coefficient along the positive direction is at least twice larger than that from the negative one. The higher the frequency of incident wave, the more obvious the difference between the two curves is. This may be reasonably explained as being the important phenomenon of asymmetric acoustic transmission. It is noteworthy that most of the acoustic waves can reach the other side of the model in the low frequency range. Owing to the wavelength of the acoustic wave at low frequency comparable to the dimension of the model, all the incident waves coming from the two directions will be diffracted by the surface of the model. As a result, the acoustic waves along opposite directions at low frequency can transmit though the model, which become virtually symmetric. Therefore, the results confirm that this model can yield an asymmetric acoustic transmission within a broad frequency band.

Fig. 3. (a) Calculated total transmission coefficients of acoustic waves that are incident from the positive (solid line) direction and the negative (dashed line) direction, respectively. The significant difference is denoted by using the blue region. (b) The rectifying ratio of the model within a broadband frequency range.

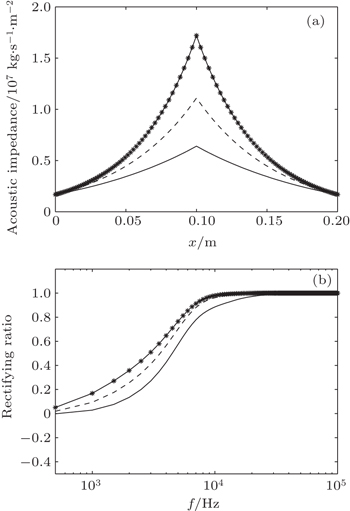
To estimate the effect of the asymmetric acoustic transmission we introduce the concept of rectifying ratio that is defined as RC=(TL − TR)/(TL+TR), where TL and TR are the transmissions along the positive and negative directions, respectively. Notice that the rectifying ratio describes the relative quantity of two transmission coefficients. Thus, as RC is equal to 1 or −1, the whole system may obtain the best effect of one-way transmission along the positive direction or the negative one. Conversely, the fact that RC equal to 0 shows that the asymmetric acoustic transmission does not exist. Figure 3(b) reveals the rectifying ratio within a broadband frequency range, corresponding to Fig. 3(a). Obviously, the curve of the rectifying ratio agrees well with the results obtained via the transmission coefficient, implying that an enhancement of the asymmetric acoustic transmission can be easily observed from 2 kHz to 100 kHz as expected. Moreover, the rectifying ratio is considerably high when the frequency of acoustic wave is over 10 kHz. This means that the efficient bandwidth of asymmetric acoustic transmission of this model is close to 90 kHz. The proposed model presents some significant advantages over the existing one, for example, a much simpler structure, broadband frequency range, more stable and realistic procedure, etc.

It is understandable that the distribution of acoustic impedance should have a direct effect on the acoustic characteristic of this structure. Thus, in order to further verify the feasibility of this model, it is necessary to choose specific acoustic impedance in an optimal manner and study the relationship between the gradient profile of impedance and asymmetric acoustic transmission. Figure 4 illustrates the comparison of the transmission coefficients among different acoustic impedances. Figure 4(a) shows three typical gradient profiles of impedance, which are designed to be of the exponential distribution but with the different maxima of acoustic impedance Zmax. It is obvious that the larger the value of Zmax, the sharper the gradient profile of impedance is.

Fig. 4. (a) Typical gradient profiles of acoustic impedance for three cases: Zmax = 6.4 × 106 kg/(s·m2), 1.1 × 107 kg/(s·m2), and 1.7 × 107 kg/(s·m2). The solid line, dashed line, and dotted line refer to the three cases (from bottom to top), respectively. (b) Comparison of rectifying ratio among the three cases (from bottom to top).

In Fig. 4(b), the acoustic impedance dependences of the rectifying ratio is also shown. The results demonstrate that the proposed model allows more acoustic waves along the positive direction to pass through as Zmax increases but blocks the acoustic waves when the transmission direction is reversed, especially in the low frequency range. This result is consistent with the previous numerical simulations. The main reason is that the fact that the gradual increase of Zmax leads to creating a more curving trajectory for acoustic wave transmission and increasing the attenuation coefficient of medium when acoustic waves are incident from the negative direction. The transmission along the negative direction is more significantly affected than along the positive one. Hence, we can obtain the more perfect low-frequency asymmetric acoustic transmission by increasing the maximum of acoustic impedance of the model. However, what is more important should be that one also needs to consider the difficulty in fabricating the medium with gradient change of acoustic impedance and the connection problem of different materials in practice when Zmax increases appropriately, rather than unnecessarily.

4. Experimental results and discussion

In order to verify the validity of the proposed asymmetric acoustic transmission structure, an experiment has been carried out by measuring the total transmission of acoustic waves that are incident from the two sides of the structure. In the present study, the medium with gradient change of impedance was prepared by the precipitation method. The details of the procedure are as follows.

The mixed metal powder and polymer binder were employed as the materials. The polymer adhesive is the mixture of phenolic resin and urotropine each with an appropriate quantity. A mixture of mixed metal powder and polymer binder was heated while continuously stirring for 30 min in a beaker. For the synthesis of individual medium, precipitation reactions were carried out using water in a plastic tube and the mixture was quickly added into it to form a mixture solution. In theory, the precipitant with different solubility products will lead to a sequential sediment process, which finally leads to precipitant particles with gradient structure. During the precipitation, a black precipitate formed, which was removed from a plastic tube and dried at 80 ° C in an oven for 2 h. The precipitates were uniaxially pressed with a pressure of approximately 80 MPa to form samples and the prepared samples were calcined at 200 ° C for 2 h inside a muffle furnace. Two cylindrical media that had the same gradient profiles of impedance were prepared with 5-cm thickness and 5.5-cm diameter. Figure 5 shows the prepared media each with a gradient change of impedance and distributions of acoustic impedance, obtained by the precipitation method.

Fig. 5. (a) Prepared media each with a gradient change of impedance. (b) Distributions of acoustic impedance of two prepared media. The dotted–solid line and dashed line refer to the first medium and the second medium as shown in Fig. 1(b), respectively.

It needs to be mentioned that due to the limited preparation technology, it is difficult to solve the intersolubility problem of the mixed metal powder and polymer solubility binder, which leads to the phenomenon that samples are easy to fracture after being calcined. Therefore, the intersolubility values of different materials and the hardness values of prepared samples were comprehensively considered. Ensuring the acoustic impedance of the medium is continuously changing, the acoustic impedance of the prepared medium increased. Figure 5(b) shows the gradient profile of acoustic impedance of two prepared samples. The acoustic impedance of prepared samples increases steadily from 4.5×106 kg/(s·m2) to 12.5×106 kg/(s·m2). Note that the distributions of acoustic impedance of two prepared samples can keep the obvious gradient changing along the thickness orientation without break. Consequently, the prepared media each with a gradient change of impedance meet the requirement of experiment.

Figure 6 schematically shows the configuration of the proposed asymmetric acoustic transmission structure. According to the structure shown in Fig. 1, the prototype of the asymmetric acoustic transmission structure is made by combining two media each with a gradient change of impedance, which are located in a cylindrical notched steel tube. The radii of the prepared media and the tube inner diameter are both 5 cm. The angle θ is 20°. The absorption rubber is chosen as the absorptive boundary. A practical cylindrical asymmetric acoustic transmission structure is eventually constructed.

Fig. 6. Cross-sectional configuration of the asymmetric acoustic transmission structure composed of two media each with a gradient change of impedance and schematic diagram of the experimental measurement system. The two media each refer to the medium with a gradient change of impedance denoted by using the blue region. The gray region represents the steel tube containing two prepared media. The red region represents the sound absorption material. A transducer and a hydrophone are chosen as the transmitter and the receiver.

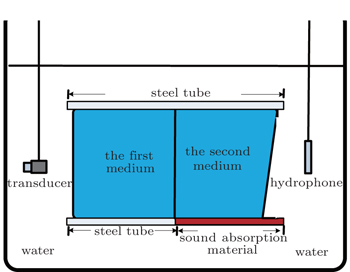
An experiment is conducted in an anechoic pool. The structure is clamped and placed between a transducer (type UAT-20W) and a hydrophone (type TC4035) which are chosen as the transmitter and the receiver, respectively. A directional transducer with ± 6° directivity angle is chosen to reduce the influences of reflection and diffraction. The emission surface of the transducer is placed vertically to the tube with a distance of 20 cm, in which the propagating acoustic waves could be regarded as plane waves. On the other side, the hydrophone is set around the tube with 2 cm. The signal is generated by the Agilent33522A signal generator for driving the transducer, and it is passed through an AR150 power amplifier. The measuring and analysis equipment also contain a B&K2636 measuring amplifier and a PULSE 3560 analyzer system.

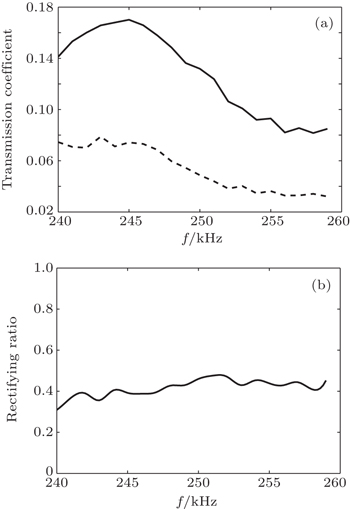
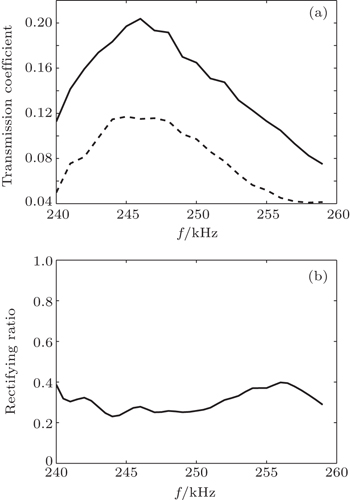
Two transmission coefficients of acoustic waves incident from the positive direction (solid line) and the negative direction (dashed line) are measured when the amplitude of acoustic wave signal is 150 mV as shown in Fig. 7(a). It can be significantly observed that the transmission coefficient along the positive direction is at least twice larger than that along the negative one within the considered frequency band ranging from 240 kHz to 260 kHz. Compared with the acoustic energy along the negative direction remarkably decreasing, much acoustic wave energy along the positive one can reach the other side of the structure in the entire frequency range. Moreover, figure 7(b) shows the measurement results of rectifying ratio within the same frequency band range. The results indicate that the curve is so flat and the rectifying ratios are all over 0.4, which are well consistent with the numerical predictions.

Fig. 7. (a) Experimental results of total transmission coefficients of acoustic waves that are incident from the positive (solid line) direction and the negative (dash line) direction, respectively, when the amplitude of acoustic wave signal is 150 mV. (b) Measurement results of rectifying ratio of the proposed asymmetric acoustic transmission structure.

To illustrate the frequency dependences of the acoustic transmissions, we further analyze the experimental results when the amplitude of the acoustic wave signal is 200 mV. It can be more clearly visualized that the obvious difference and rectification effects appear in Fig. 8. It is worth noting that the rectifying ratio obtained by experimental measurement is not so large as one obtained by the numerical prediction in the high-frequency range. In fact, this might be primarily due to the inevitable impedance mismatch between the water and the surface impedance of the prepared medium. The problem that the surface impedance of the prepared medium is three times larger than the impedance of water necessarily leads to acoustic wave reflection significantly appearing at the boundary of the structure. On the other hand, another possible explanation for this phenomenon lies in the scattering and diffraction effect caused by the steel tube and the rods of the structure. According to the numerical and experimental results, the proposed structure composed of two media each with a gradient change of impedance is proved to be capable of rectifying the directions of incidence acoustic waves and achieving a satisfactory broadband one-way transmission.

Fig. 8. (a) Experimental results of total transmission coefficients of acoustic waves that are incident from the positive (solid line) direction and the negative (dashed line) direction, respectively, when the amplitude of the acoustic wave signal is 200 mV. (b) Measurement results of rectifying ratio of the proposed asymmetric acoustic transmission structure.
5. Conclusions

In this paper, we present an underwater asymmetric acoustic transmission structure by using the medium with a gradient change of impedance. The model of asymmetric acoustic transmission is established and the basic mechanism is investigated based on the acoustic ray theory and transfer-matrix method. The simulation results reveal that the proposed structure can yield a satisfactory broadband asymmetric acoustic transmission. The characteristic of asymmetric acoustic transmission is sensitive to the gradient profile of acoustic impedance. The medium of gradient change of impedance is prepared by the precipitation method. The experimental results verify the validity and efficiency of the proposed structure, and agree well with the numerical predictions. Therefore, this asymmetric acoustic transmission structure has potential applications in various underwater practical situations such as weakening vibration and reducing noise, filters, and transducers.

Reference
1Takeda HJohn S2008Phys. Rev.93023804
2Yu ZWang ZFan S 2007 Appl. Phys. Lett. 90 121133
3Li B WWang J 2004 Phys. Rev. Lett. 93 184301
4Chang C WOkawa DMajumdar AZettl A 2006 Science 314 1121
5Liang BYuan BCheng J C 2009 Phys. Rev. Lett. 103 104301
6Liang BGuo X STu JZhang DCheng J C 2010 Nat. Mater. 9 989
7Gu Z MLiang BCheng J C 2013 Chin. Phys. B 22 014303
8Zhu X FZou X YLiang BCheng J C 2010 J. Appl. Phys. 108 124909
9Yuan BLiang BTao J CZou X YCheng J C 2012 Appl. Phys. Lett. 101 043503
10Li R QLiang BLi YKan W WZou X YCheng J C 2012 Appl. Phys. Lett. 101 263502
11Cai CZhu X FChen QYuan YLiang BCheng J C 2011 Chin. Phys. B 20 116301
12Lin S C SHuang T J 2009 J. Appl. Phys. 106 053529
13Lin S C STittmann B RHuang T J 2012 J. Appl. Phys. 111 123510
14Lin S C SHuang T JSun J HWu T T 2009 Phys. Rev. B 79 094302
15Liu B SLei J Y1993Underwater Acoustic TheoryHarbinHarbin Engineering University Press113(in Chinese)
16Pedersen C PTretiak OHe P 1982 J. Acoust. Soc. Am. 72 327