† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51305448 and 51275519).
This paper presents a semi-analytical solution for the vibration and sound radiation of a semi-infinite plate covered by a decoupling layer consisting of locally resonant acoustic metamaterial. Formulations are derived based on a combination use of effective medium theory and the theory of elasticity for the decoupling material. Theoretical results show good agreements between the method developed in this paper and the conventional finite element method (FEM), but the method of this paper is more efficient than FEM. Numerical results also show that system with acoustic metamaterial decoupling layer exhibits significant noise reduction performance at the local resonance frequency of the acoustic metamaterial, and such performance can be ascribed to the vibration suppression of the base plate. It is demonstrated that the effective density of acoustic metamaterial decoupling layer has a great influence on the mechanical impedance of the system. Furthermore, the resonance frequency of locally resonant structure can be effectively predicted by a simple model, and it can be significantly affected by the material properties of the locally resonant structure.
Attaching an elastic decoupling layer to a vibrating structure immersed in water represents a common way to reduce the sound radiation of the vibrating structure. This treatment is effective to isolate the fluid from vibrations of the structure by reason of mismatching between water and decoupling layer and mismatching between decoupling layer and the plate.
Sung has explored the use of air-voided elastomer decoupling layer in reducing noise of flexible plate.[1] His research ensures that the amount of noise reduction increases as the thickness of the decoupling layer, the speed of dilatational wave, and dilatational wave’s loss factor increases, while the effects of shear wave speed are insignificant.
Berry and Foin have investigated the forced response and the sound radiation of decoupled plates with three-dimensional elasticity model. Their research shows that shear wave components in the decoupling material usually have little effect on the sound radiation in a heavy fluid.[2] Wang’s experiment shows that calculation result of three-dimensional elasticity model and test results coincide well with each other.[3]
In order to increase the effectivity of noise reduction, cavities with different shapes have always been embedded into decoupling layer with the increase of impedance mismatching. Tao et al. have investigated a sound radiation model of an infinite plate coved with a void decoupling layer.[4] Their analysis indicates that primary mechanism of the noise reduction in their model is the vibration isolation in the decoupling layer. Zhu et al. make an experimental and numerical investigation about the sound radiation of the floating structures covered with chiral layer.[5] Their results show that chiral layer can effectively reduce underwater sound radiated by the structure. Huang et al. have investigated decoupling mechanism of a viscoelastic decoupling layer with horizontal cylindrical cavities.[6] Their study shows that the decoupling layer with horizontal cavities can greatly enhance the mechanical impedance and suppress the mean square velocity of vibrating structure. On the other hand, the decoupling layer with horizontal cavities has larger impedance mismatch with water than the decoupling layer without them, thus it brings more vibration transmission loss.
Although traditional decoupling layer has an excellent performance on noise attenuation at high frequencies, it should be mentioned that they have little effect at low frequencies. In some cases, noise radiated by structure with decoupling layer may increase at low frequencies.[4,6]
Locally resonant metamaterials (LRM) have been introduced by Liu et al. as a conceptual realization of an acoustic metamateria.[7,9] LRM has been used as an effective way to control subwavelength waves at low frequencies. In recent years, localized resonances in phononic crystals have been introduced to improve the low-frequency acoustic absorption of viscoelastic materials.[10,11] Zhao et al. investigated the acoustic absorption of viscoelastic slabs embedded with resonant sonic materials.[12] Their theoretical and experimental studies indicate that locally resonant sonic materials have an outstanding performance of sound absorption. Wen et al. later used finite element method (FEM) to reveal the absorption mechanism.[13] Their study presents that localized resonance leads to the absorption peak. Jiang et al. introduced woodpile structure into LRM, and used it in underwater acoustic absorbing material. Their structure shows an excellent performance on acoustic absorbing in their research.[14] Duan et al.[15] demonstrate that perfect absorption of elastic wave can be achieved by ultra-thin elastic meta-films when the boundary is a free space or a hard wall. And the pure imaginary effective mass density condition which is used for perfect absorption can be achieved by elastic metamaterials with large damping.
Much work has been conducted to investigate the sound absorption of the LRM, but little has been done about the noise reducing capability of the LRM when it is attached to the surface of vibrational underwater structure. In this paper, a semi-analytical formulation of the sound radiation from an underwater semi-infinite plate covered by a decoupling layer embedded with LRM is investigated. In the formulations, effective medium theory is adopted to obtain the equivalent properties of the decoupling layer with LRM, thereby elastic theory can be applied to the decoupling layer. In addition, the base plate in this work is dealt with classic plate theory. A solution of the vibration and sound radiation is derived from the composite system with simply supported boundary conditions. The proposed method is verified by the consistency between the predictions by FEM and the method in this paper. By using the mechanical impedance and modality theory, the vibration and sound radiation characteristics of the decoupling system are further examined.
Figure
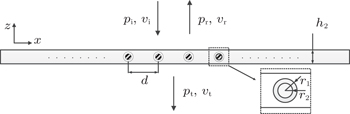
For brevity, the time-harmonic dependence of the form eiωt is assumed. The acoustic pressure of incident wave can be expressed as[16]

According to Bloch theorem for periodic systems, the discrete translational symmetry with period d in the x direction means the physical fields χ(x,z) satisfying the Bloch condition:
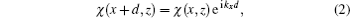
In the incident acoustic field, the wave zone includes incident wave and reflected wave:

The sound pressure of the reflected wave can be expressed as:
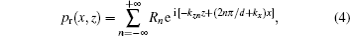
The sound pressure of transmitted wave can be expressed as:

Using the FEM and Bloch theorem, the model of infinite structure with periodic cell can be constructed by just one cell with periodic boundary, and the equation of the acoustic-fluid-structure coupling can be expressed as[17]
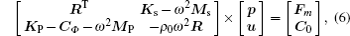
It can be noted that the velocity v in systems satisfies the relation: v = iωu, so the amplitude of the sound pressure p1, the velocity v1 on the intersection plane of the viscoelastic polymeter slab with the incident acoustic field, and the amplitude of the sound pressure p2, the velocity v2 on the intersection plane of the viscoelastic polymeter slab with the transmission field and can be solved in Eq. (

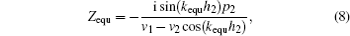
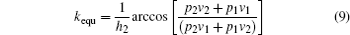
Figure
After decoupling layer is treated as effective homogeneous material, the dynamical equation of decoupled plate could be expressed with elastic theory as:
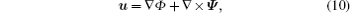
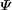
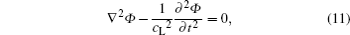

The boundary conditions for the base plate which is simply supported on the lateral sides are:
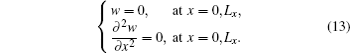
Equation (
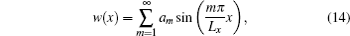
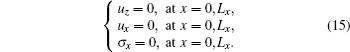
The scalar potential of the decoupling layer can also be expressed in terms of similar trigonometric functions

Substituting Eq. (
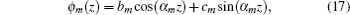
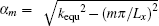
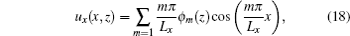


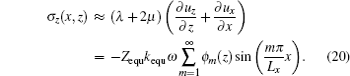
The boundary conditions at the plate/decoupling layer interface can be expressed as
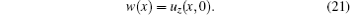
The boundary conditions at the decoupling/water interface are
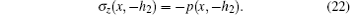
This boundary conditions express the continuity of the stress between the plate and the decoupling layer. The acoustic pressure in the fluid half-space can be calculated by Rayleigh integral
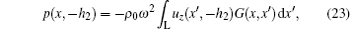
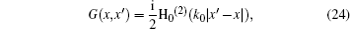
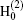
Substituting Eqs. (
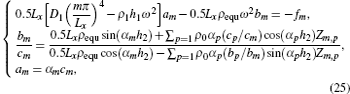
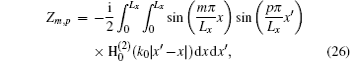
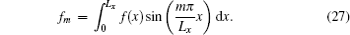
Therefore, am, bm, and cm can be solved from Eq. (
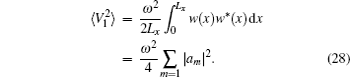
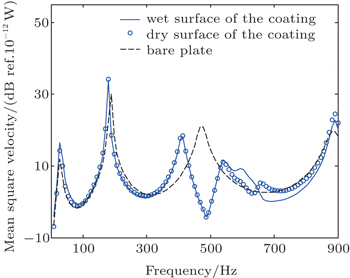
The mean square velocity of the outer surface of decoupling layer is defined by
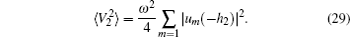
The sound power radiated by outer surface of the system in the water is

In order to confirm the validity of the proposed method in this paper, the result calculated by FEM (calculated by Comsol4.4) is compared with the present method, as shown in Fig.
Figure
In Fig.
Furthermore, the calculation time of paper’s method is much shorter than the FEM. The finite structure’s sound radiation which is calculated by FEM directly must build up the model with all the cells in the structure. And the model should also contain fluid field which must be big enough to simulate semi-infinite sound field. In paper’s method, the calculation of the transmission model which is used for getting effective properties just need only one cell with the periodic boundaries being set. And the sound radiation is calculated by theory method of which the calculation time can be neglected.
The calculation results also show that radiation power of the decoupling system has an obvious reduction at about 490 Hz which has little relation with the exciting position. According to the decoupling mechanism,[6,20] the reduction of the radiation power can mostly be ascribed to the isolation of vibration or restraining base plate’s vibration by attaching decoupling layer.
Figure
The base layer’s velocity of order m without decoupling layer can be expressed as:
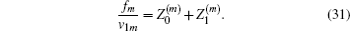


In Eqs. (


In Eqs. (
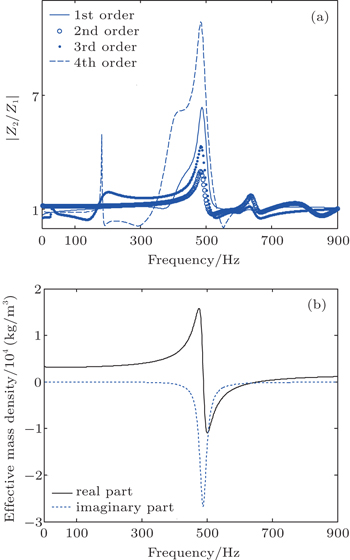
Figures
Now that system’s vibration can be restrained by decoupling layer with periodic LRS, the noise reduction’s frequency could also be regulated on the basis of the LRS’s characteristic. Figure
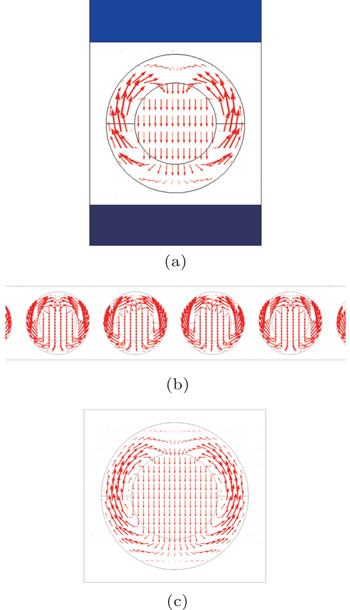 | Fig. 6. The displacement amplitude fields at resonant frequency (a) transmission coefficient model, (b) radiation model, (c) natural frequencies model. |
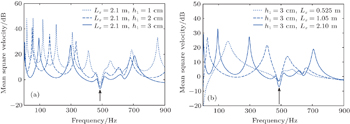 | Fig. 7. Mean square velocity of dry surface of the system with (a) different thicknesses and (b) different lengths. |
Figure
This paper presents an analysis of vibration and sound radiation influence of the decoupling layer with periodic LRS. A theoretical calculation model for the decoupled plate with periodic LRS has been developed based on the use of effective medium theory and elastodynamics theory. Such a model is more efficient than conventional finite element model and shows adequate accuracy for acoustic analysis in preliminary design. The numerical analysis gives the following findings:
Decoupling layer with LRSs can significantly reduce the sound radiation of underwater plates around the LRS’s resonance frequency. The performance of sound radiation reduction is mostly caused by the suppression of base plate vibration. The additional mechanical impedance of the system is directly dependent on the effective density of decoupling layer. The shake-up of effective density around local resonance frequency greatly effects system’s mechanical impedance and thus suppresses the vibration of base plate. The vibration suppression properties of decoupling layer could be guaranteed for different sizes of base plate. The locally resonant structures involved in the radiation prediction model and transmission prediction model, have similar vibration modalities. A simple model can be adopted to predict the local resonance frequency of the decoupling layer with LRS. The local resonance frequency decreases as the density of the core increases and increases as the transverse wave velocity of the coating increases.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 |