|
|
† Corresponding author. E-mail:
Atmospheric duct is a common phenomenon over large bodies of water, and it can significantly affect the performance of many radio systems. In this paper, a two-month (in July and August, 2014) sounding experiment in ducting conditions over Bosten Lake was carried out at a littoral station (41.89° N, 87.22° E) with high resolution GPS radiosondes, and atmospheric ducts were observed for the first time in this area. During the two months, surface and surface-based ducts occurred frequently over the Lake. Strong diurnal variations in ducting characteristics were noticed in clear days. Ducting occurrence was found at its lowest in the early morning and at its highest (nearly 100%) in the afternoon. Duct strength was found increasing from early morning to forenoon, and reaching its maximum in the afternoon. But contrarily, duct altitude experienced a decrease in a clear day. Then the meteorological reasons for the variations were discussed in detail, turbulent bursting was a possible reason for the duct formation in the early morning and the prevailing lake-breeze front was the main reason in the afternoon. The propagation of electromagnetic wave in a ducting environment was also investigated. A ray-tracing framework based on Runge–Kutta method was proposed to assess the performance of radio systems, and the precise critical angle and grazing angle derived from the ray-tracing equations were provided. Finally, numerical investigations on the radar performance in the observed ducting environments have been carried out with high accuracy, which demonstrated that atmospheric ducts had made great impacts on the performance of radio systems. The range/height errors for radar measurement induced by refraction have also been presented, too, which shows that the height errors were very large for trapped rays when the total range was long enough.
As an anomalous propagation mechanism in the marine troposphere or above other large bodies of water, atmospheric ducts can significantly affect the electromagnetic wave (EMW) propagation from the UHF band to sub-millimeter wave, which would lead to some unexpected effects for radars, high power microwave (HPM), GPS, wireless communication systems, and so on, such as extending the maximum detection range of radars, enhancing radar clutter, creating radar holes (or shadow zone), and causing positioning errors.[1–3] So an accurate knowledge of the ducting information will be needed to assess the performance of radio systems, especially for radar and HPM.
Atmospheric duct frequently occurs over oceans, seas, and coastal areas all over the world where humidity decreases rapidly with altitude. The most famous ducting area is the Persian Gulf which is entirely surrounded by desert landmass. Lots of pages of scientific research about the local boundary layer conditions have been published until now.[3–5] In Europe and South Asia, the ducting conditions over the Baltic Sea,[6,7] the English Channel,[8,9] the Mediterranean region,[10] and the Indian Ocean[11] have been reported. As for China, lots of investigations have been made on the ducting conditions over the East China Sea and South China Sea during the last two decades.[12–16] In recent years, a ship-based ducting measurement both over the South China Sea and the Eastern Indian Ocean has been reported.[17] The horizontal inhomogeneity of evaporation ducts and their impact on the EMW propagation has also been reported.[18] However, previous researches were always focusing on the large seas around the world; fewer researches have been done with the endorheic lakes, especially for Qinghai Lake and Bosten Lake in China. In this paper, a short-term meteorological sounding experiment was carried out over Bosten Lake during July and August, 2014, and the clear-air ducting conditions over the Lake are shown for the first time. Then a ray tracing framework for modeling EMW propagation based on Runge–Kutta method is presented.
During the last two decades, although two new important techniques have been developed to determine ducts over large bodies of water, i.e., Simulated Model based on numerical weather prediction (NWP) techniques[18–20] and refractivity from radar clutter (RFC) technique,[21–24] there were some disadvantages about the two techniques. As showed by Guo X M et al.,[15] the predicted duct altitudes via NWP techniques were not so accurate compared with the direct measuring results. As for RFC technique, the accuracy of the estimated refractivity heavily depends on a priori information that given.[24] In this work, we would employ the conventional way using modern high-resolution GPS radiosonde to determine the vertical refractivity profiles over Bosten Lake, which will be shown in Section 2. The duct characteristics, i.e., ducting occurrence, duct strength, and layer thickness, will be shown in that section, as well as the diurnal variation of ducts. In Section 3, meteorological reasons for diurnal ducting variation will be given. In Section 4, we will present a ray tracing framework for modeling EMW propagation, and then a rigorous result about the EMW propagation characteristics in a ducting layer, i.e., critical angle and grazing angle, will be given. Finally, a simulating result of EMW propagation under the existed ducting environments over the Lake will be presented with high accuracy.
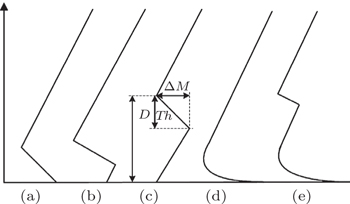
As one of the largest inland freshwater lakes of China, Bosten Lake, which is located in the southern part of Xinjiang Uygur Autonomous Region, covers an area of nearly 1200 km2, its maximum dimensions are about 56 km in length and 25 km in width, and the Lake surface is about 1048 m high above the sea level. It is entirely surrounded by Gobi-desert landmass, which is similar to the Persian Gulf, and a temperate desert climate prevails in the area all around generally. Previous studies stated that atmospheric ducts can be easily formed by advection of warm, dry air coming from the desert over cooler water,[4,5,25] thus from this point of view, the Lake is a high-occurrence ducting area theoretically. Ducting conditions predict negative vertical gradient of modified refractivity as a result of strong gradients of temperature and humidity in the atmosphere. The modified refractivity M is defined by the empirical equation
 | Fig. 1. Idealized M-profiles of (a) surface duct, (b) surface-based duct, (c) elevated duct, (d) evaporation duct, and (e) complex duct. The duct altitude D, duct thickness Th, and duct strength ΔM are illustrated on elevated duct. |
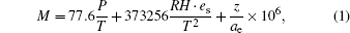
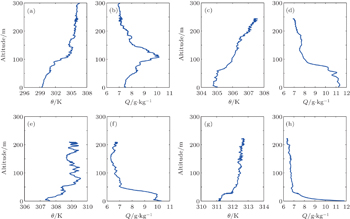
Conventionally, meteorological data, i.e., atmospheric pressure P, temperature T, and humidity RH, can be determined via radiosonde sounding measurement. In this work, a modern high resolution GPS radiosonde (Changfeng CF–06–A[26]) tied to a carrier of captive balloon was employed to measure meteorological parameters at different altitudes. Compared with classical ones, GPS radiosondes have higher vertical resolution (sampled at 1-s intervals) which would make the diagnosis of small scale duct structures possible.[17,26] The use of captive balloon can provide a much higher vertical resolution of less than 1 meter by controlling the carrier’s ascent rate manually, which outclasses the resolution of Vaisala RS products used in EU and India.[11,27] All the radiosondes were launched over a new littoral station (41.89° N, 87.22° E) on the south bank of the Lake, just near the bottle-neck between the main lake and the small adjacent lake in the southeast corner. In this paper, the maximum height to which the balloon went was limited to 500 m, which was high enough for us to detect almost all of the ducting events over the Lake. Since the specific humidity Q decreases sharply (the most important reason for which ducting events happen) within the first 200-m layer over the Bosten Lake Basin according to an analytical result of historical radiosonde data recorded at a classical radiosonde station which lies more than ten kilometers southeast of the littoral station, which is shown in Fig.
 | Fig. 2. The mean (a) potential temperature θ and (b) specific humidity Q in August, 2014 over the classical radiosonde station. Typical profiles of (c) potential temperature θ and (d) specific humidity Q observed over the two stations on 11 August 2014 at 2000-h CST. Lines with circles represent the profiles observed over the classical radiosonde station, and lines with stars represent the profiles observed over the littoral station. |
It should be emphasized that there is a discrepancy between the local time (LT) and China Standard Time (CST), that is LT = CST-0200 h, and the high noon at the local area is about 1400-h CST. As a general rule in China, CST will be used in this paper. On the basis of the weather conditions in a day over the Lake, days are divided into early morning (0800-h to 1000-h CST), forenoon (1000-h to 1400-h CST), and afternoon (1400-h to 2100-h CST, i.e., between the noon and sunset). The sounding experiments began on 15th July and finished at the end of August. Because of some technical reasons, only a few data were collected during July. All of the radiosondes were launched on clear days and majority of these radiosondes were launched during the forenoon with a time interval about one hour or two. Similar to Zhao Xiao-feng et al.,[17] we employed several data quality control methods to eliminate unreasonable measurements before taking statistics. Evident inaccurate datasets were eliminated at the first sight, and singular points, which were common for high-resolution GPS radiosonde measurements, were eliminated by a Kernel smoother. For points with a great difference between measurements and smoothing results were eliminated.
During the two months, 102 datasets were obtained, six of which were invalid. For each dataset, M-profiles were calculated from temperature, pressure, humidity, and altitude via Eq. (
 | Fig. 3. M-profiles for several types of ducts observed over Bosten Lake in 2014: (a) surface duct observed on 26 July at 1140-h CST; (b) surface-based duct observed on 7 August at 1130-h CST; (c) evaporation duct observed on 28 August at 1230-h CST; (d) elevated duct observed on 22 August at 0830-h CST; (e) complex duct observed on 1 August at 1820-h CST; (f) standard atmosphere condition observed on 1 August at 1140-h CST. |
Ducting occurs when the gradient of modified refractivity, i.e., dM/dz, turns negative. Fortunately, all the five types of ducts mentioned earlier were observed over the Lake, which are illustrated in Fig.
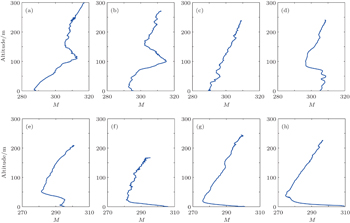
Ducting conditions are significantly influenced by the meteorological conditions. As for Bosten Lake, it experiences a strong diurnal variation in air temperature and humidity during the daytime; therefore there will be significant variations in the ducting occurrence, duct altitude, duct strength, and its thickness. Figure
 | Fig. 4. Ducting variations on 22 August 2014: (a) observed at 0830-h CST, (b) observed at 1030-h CST, (c) observed at 1130-h CST, (d) observed at 1220-h CST, (e) observed at 1410-h CST, (f) observed at 1610-h CST, (g) observed at 1820-h CST, (h) observed at 2000-h CST. |
As mentioned earlier, 78 ducting events were observed within the 96 valid datasets obtained during the two-month experiments. Table
According to Table
 | Table 1. Distribution of ducting events during daytime along with number of datasets. . |
Besides the ducting occurrence, other duct characteristics, i.e., duct altitude, duct strength, and duct thickness, are very important while assessing the EMW propagation, for they determine the trapping capability of a duct. The mean duct altitude, duct thickness, duct strength, and their corresponding standard deviations in every part of a day during the two months are listed in Table
| Table 2. Statistical results of duct characteristics during a day. . |
From Table
Briefly, the ducting conditions experienced a strong diurnal variation in a clear day during the two months. In a clear day, the ducting occurrence increases from early morning to forenoon, and then reaches nearly 100% in the afternoon. Similarly, the duct strength increases from early morning to forenoon, and then reaches its maximum in the afternoon. Higher altitude duct (as well as thicker duct) is observed in the early morning when elevated ducts may occur, then followed by forenoon, and becomes lower in the afternoon when surface ducts prevail.
In the preceding section strong diurnal variations in ducting condition are noticed in clear days. The main reason for the strong diurnal variations is large diurnal changes in air conditions, i.e., potential temperature and specific humidity over the Lake.
In a calm, early morning of a clear day in the two hottest months (July and August) in Bosten Lake Basin, just during the two more hours after the sunrise, temperature inversion resulting from radiative cooling of the surface still keeps alive with an altitude of several hundred meters, which is favorable for the formation of a stable boundary layer (SBL). Since the surface is emitting more radiation energy than it is receiving from solar radiation during that time. The strong stability in an SBL will suppress the vertical convection of water vapor, so the specific humidity in a radiation inversion layer will vary slowly with height generally, a sharp decrease at high altitudes is unusual, but as shown earlier, elevated duct might happen in the early morning. As an accepted scenario, the main reason for the formation of elevated ducts is subsidence motion[4,5,11,16] which can last for several days, but some observed elevated-duct cases did not predict subsidence motion, such as the elevated duct observed on 22 August 2014, and why this happened? Stull R B[28] and Ohya Y et al.[29] indicated that occasional bursting of turbulence could be found in a SBL with strong stability, and a turbulent bursting would cause sporadic vertical mixing. If a bursting event occurs on the ground or lake surface, it will bring an abundance of water vapor upward at a high altitude over the Lake due to buoyancy, and the temperature inversion will prevent it from diffusing into a higher layer above the inversion layer. When water vapor associated with turbulence bursting advect over the Lake, an elevated duct will occur. Sun J L et al.[30] have once observed that a solitary wave with high specific humidity was propagating in a nocturnal SBL at Leon, Kansas, USA in October 1999. The elevated duct observed in the early morning of 22 August has certainly resulted from turbulent bursting, for an obvious potential temperature inversion (the so called overturn) was observed at a depth of about 150 m (see Fig.
Contrary to temperature inversion, a potential temperature inversion is defined as a localized decrease of potential temperature versus height, which is generated by turbulence or Kelvin–Helmholtz billows.[31] As illustrated in Fig.
 | Fig. 5. Typical profiles of potential temperature θ and specific humidity Q observed on 22 August 2014: (a) potential temperature and (b) specific humidity profiles observed at 0830-h CST; (c) potential temperature and (d) specific humidity profiles observed at 1220-h CST; (e) potential temperature and (f) specific humidity profiles observed at 1410-h CST; (g) potential temperature and (h) specific humidity profiles observed at 2000-h CST. |
As time passes, the surface receives more energy from solar radiation than emitting radiation, then the surface heats the air continually, at last, the inversion will be eliminated in the mid-morning, air temperature will decrease linearly near the surface, so does the specific humidity, as a result, standard atmosphere will be observed, which is shown in Fig.
After the noon, lake-breeze prevails along the lakeshore line, and becomes stronger and stronger as time passes in the afternoon, which is the main reason for the ducting formation during that time. Cool air from the Lake moves across the warm land near the lakeshore line with a velocity of several meters per second, a return circulation (the anti-lake-breeze) aloft brings the warmer, low-humidity air back to the middle of the Lake where it descends toward the Lake surface to close the circulation,[28,32,33] as a result, a temperature inversion with a depth less than 100 m and an increase in humidity over the warm land near the lakeshore line will be formed, which is depicted in Figs.
To assess the performance of radar or HPM in a ducting environment, an EMW propagation model must be provided. Although parabolic wave equation method are widely used to model the field distribution of EMW, ray-tracing can provide a rather intuitive tool for modeling the propagation characteristics, such as propagation paths, critical angle, shadow zone, refraction angle, grazing angle, and etc.,[34,35] which is also widely used in recent years, too.[2,35] However, most of the previous methods for ray-tracing were based on small angle approximation, here we will present a ray-tracing technique based on Runge–Kutta method.
Consider a ray passes through a stratified atmosphere above a spherical Earth where refractive index n depends on the height above the Earth’s surface H only, the path of a radio wave will obey the Snell’s law
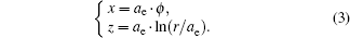
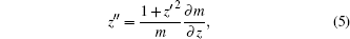
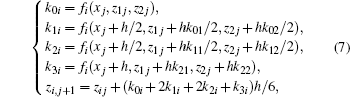
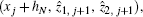
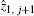
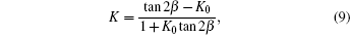
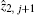
Furthermore, equation (
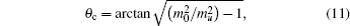
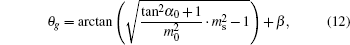
Additionally, assume that the target is located at (xT, zT) in the new coordinate, the refractive errors of the range ΔR and height ΔH for radar measurement can be calculated,
To visualize the ducting effect on the radar or HPM performance, here we will show some simulation results about EWM propagation in the ducting environments observed over the Lake (shown in Fig.
| Table 3. Parameters in the simulation and the corresponding ducing characteristics. . |
Figure
As for the simulations illustrated in Fig.
 | Fig. 6. EWM propagation in different environments: ray-tracing paths in (a) surface ducting environment, (b) surface-based ducting environment, (c) evaporation ducting environment, (d) elevated ducting environment, (e) standard atmosphere environment, and (f) surface-based ducting environment over irregular terrains. The left panels show the corresponding M-profiles normalized from Fig. |
The ray tracing method present in this work is a convenient tool to assess the performance of radar, HPM or communication systems in a ducting environment which can provide a rather intuitive picture for EMW propagation, as well as some precise propagation characteristics. In addition, we compared the square of the first derivative of z (i.e., p2 in Eq. (
| Table 4. Range/height errors of radar measurement in a surface duct. The values in the bracket represent the refractive height errors of radar measurement. . |
The effect of the atmospheric ducts upon EMW propagation is important for many radio systems. In this paper we present a two-month (in July and August, 2014) observation of the atmospheric ducts over Bosten Lake using high resolution GPS radiosonde for the first time. Strong diurnal variation in ducting characteristics is noticed in a clear day and the features of the ducting environments are discussed in detail. Ducting occurrence increases from early morning to forenoon, and then reaches its maximum (nearly 100%) in the afternoon. So does the duct strength. But contrarily, duct altitude experiences a decrease in a clear day. The main reason for the diurnal ducting variation is as follows:
In the early morning, radiative inversions do exist, thicker SBL will suppress the convection of water vapor, a possible reason for duct formation is turbulent bursting which means a lower ducting occurrence and weaker duct strength, and elevated duct may occur at that time, which means that higher altitude duct and thicker duct will be observed. During forenoon, evaporation becomes stronger, vertical air motion dominates in the surface layer, then the ducting occurrence and duct strength will increase, duct altitude and thickness will decrease. After the noon, lake-breeze prevails over the lakeshore, thinner and stronger front inversion layer will last for several hours, thus, the ducting occurrence and duct strength reaches their maximum in a day. Surface duct dominates during that time, which means a lower duct altitude and thinner duct thickness.
A novel ray-tracing framework based on Runge–Kutta method is present to assess the performance of radio systems in a ducting environment, and precise critical angle and grazing angle for a duct derived from the ray-tracing equations are provided. The range/height errors for radar measurement induced by refraction has also been presented, too. Numerical experiments on EMW propagation in the observed ducting environments with the ray-tracing framework have been carried out with high accuracy. The results of the numerical investigations have demonstrated the significant influence on radio systems of atmospheric ducts, for example ray trapping, beam splitting, detecting shadow, refractive errors, and so on.
This study will also serve as a complementary study of atmospheric duct for the endorheic lakes in Xinjiang Uygur Autonomous Region. In future studies, ducting conditions in other seasons would be investigated, and new technique for determining ducts can be used.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 28 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 |
