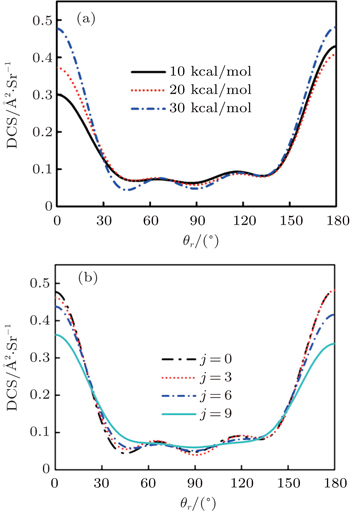
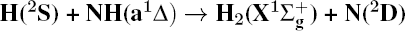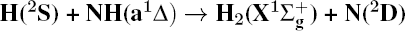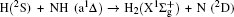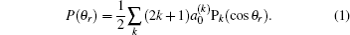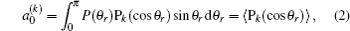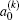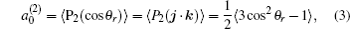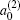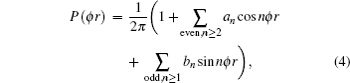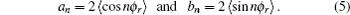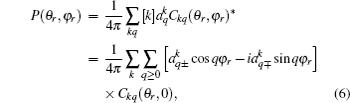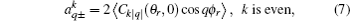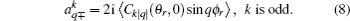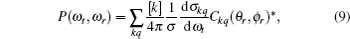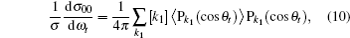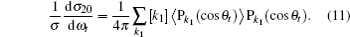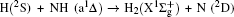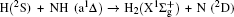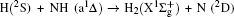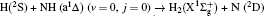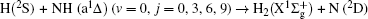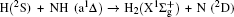1. IntroductionThe reaction H + NH → H2 + N has played an important role in the chemistry of nitrogen containing fuels, the catalyst realm and the renewable energy production.[1] Owing to their significant effects, the ground and first excited electronic state of NH2 have been studied quite extensively by various experimental[2–5] and theoretical techniques.[6–33] In the previous theoretical studies, most of them mainly forced on the dynamic behaviors of the ground and first excited state NH2. In this case, such studies have often been concentrated on the scalar properties of the H + NH → H2 + N reaction. To comprehensively understand the NH2dynamics, it is insufficient to investigate only the scalar properties. Vector correlation can provide the detailed information about the whole atom motion when reaction occurs, which can help experimentalists rationalize the experimental results. So it is important to study not only their scalar properties, but also their vector properties. The most familiar vector correlation between the reagent and product relative velocity (k, k′) is characterized by the differential cross-section dσ/dωt (DCS), and the most important vector correlation is the correlation among three vectors k, k′, and j′ (the product rotational angular momentum). The correlations among the three vectors in the center-of-mass (CM) frame can be characterized by certain interesting double and triple vector correlations.
In order to fully comprehend the excited-state property of NH2 reaction Li and Varandas[6] reported an adiabatic PES of NH2 first excited state 12A′ based on the double many-body expansion (DMBE) theory. In the present work, the quasi-classical trajectory (QCT) method is used to mainly explore the vector correlations (such as P(θr), P(ϕr), and P(θr, ϕr)) based on the first excited state NH2(12A′) DMBE-SEC PES.[6] We select three different collision energies (10, 20, and 30 kcal/mol) to investigate the influences on stereodynamics with v = 0 and j = 0. In turn, four different initial rotational levels (j = 0, 3, 6, 9) are chosen to further study the different effects originating from rotational excitation under the collision energy 30 kcal/mol with initial vibrational level v = 0. The rest of this paper is organized as follows. In Section 2 we briefly review the theoretical methodologies adopted in the current study. In Section 3 we present and discuss the calculated results. Finally, in Section 4 we draw some conclusions from the present studies.
2. Theory2.1. Quasi-classical trajectory calculationsThe accurate first excited state 12A′ PES constructed by Li and Varandas[6] is adopted in the present calculations. The calculation method of QCT is the same as that in Refs. [7]–[12]. In this work, three different collision energies (10, 20, and 30 kcal/mol) are selected to investigate the influences on stereodynamics with v = 0 and j = 0. In turn, four different initial rotational levels (j = 0, 3, 6, 9) are chosen to further study the different effects originating from rotational excitation under the collision energy 30 kcal/mol with v = 0. The classical Hamilton equations are numerically integrated in three dimensions. In our calculations, the integration step is set to be 0.1 fs to ensure a conservation of the results. In order to ensure no interaction between attacking atom H and the center-of-mass (CM) reference frame of the diatomic molecule NH, the distance between them is set to be 15 Å. A total of 3 × 104 trajectories are sampled, and the appropriate value of the maximum impact parameter is selected after preliminary running batches of 3×103 trajectories at each collision energy. The orientation of the diatomic molecule and the phase of the diatomic vibrational motion are randomly sampled by a Monte Carlo procedure. Moreover, the impact parameters are optimized before running the trajectories. That is to say, the initial azimuthal angle and polar angle of the reagent molecule internuclear axis are randomly sampled based on Monte Carlo method, and the range of the angles is from 0° to 180° and from 0° to 360°, respectively.
2.2. Vector correlationsThe CM reference frame is used in the present investigation. The reagent initial relative velocity vector k is parallel to the z axis in the CM frame. Scattering plane x–z contains k and final product’s relative velocity vector k′. Scattering angle θt is the angle between k and k′. The azimuthal and polar angles describing the direction of the final rotational angular moment j′ are ϕr and θr, respectively.
The distribution function of P(θr) describing the k–j′ correlation can be expanded in a series of Legendre polynomials as follows:[34–43]
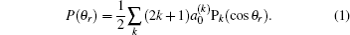
The coefficients of the expansion are given by
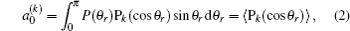
when
k is odd,
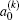
is called orientation parameter, and when
k is even, it is called alignment parameter. For
k = 2, the coefficient of the expansion is
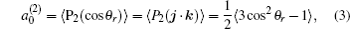
which gives a simple way to express the degree of the product rotational alignment effect, and
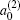
is called the rotational alignment parameter of the product.
The dihedral angle distribution function of P(ϕr) describing the k–k′–j′ correlation can be expanded in a Fourier series[34–43]
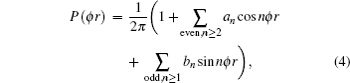
where
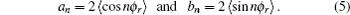
The joint probability density function of angles θr and ϕr, which determine the direction of j′, can be expressed as
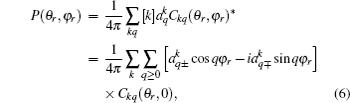
where [
k] = (2
k + 1), and the polarization parameter is expressed as
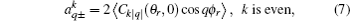
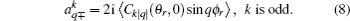
The full three-dimensional angular distribution associated with k–k′–j′ can be represented by a set of generalized polarization dependent differential cross-sections (PDDCSs) in the CM frame that is described in Refs. [34]–[43]. The fully correlated CM angular distribution is written as
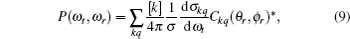
where
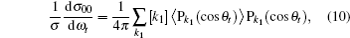
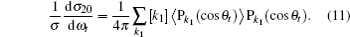
3. Results and discussion3.1. k–k′ vector correlationsFigure 1 shows the global k–k′ angular distribution for the DMBE-SEC PES. The calculated DCS values for the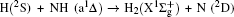 
reaction at three collision energies are displayed in Fig. 1(a). It is clearly shown that the HH molecules are scattered mainly in the broad forward and backward. A similar forward-backward scattering has been reported by Peyerimhoff and Buenker in the NH2 ground state PES.[15] With the increase of the collision energy, both forward scattering and backward scattering become higher, in which the forward scattering has a bigger magnitude of variation. According to the capture model,[44] it may be easy to understand that the forward scattering increases with the increase of collision energy. The influence of collision energy on the k–k′ distribution can be attributed to a purely impulsive effect. At higher energies, more repulsive regions of the surface become available. More repulsive parts of the PES energetically accessible are not compensated for by increasing the collision energies, resulting in a forward scattering tendency with the increase of collision energy. The variations of the k–k′ angular distribution with rotational level (v = 0, j = 0, 3, 6, 9) for NH molecular at collision energy of 30 kcal/mol are shown in the plot of Fig. 1(b). As can be seen in Fig. 1(b), both forward and backward scattering become lower with the increase of rotational quantum number. It could be explained as the fact that the rotational excitation enlarges the rotational rate of reagent NH in the entrance channel, which reduces the probability of collision between incident H atom and H atom of target molecular, resulting in both forward and backward scattering becoming lower.
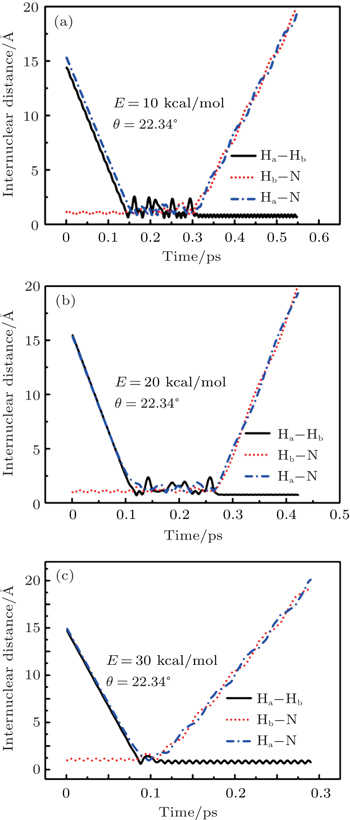
To obtain a clearer understanding of the reaction mechanism, the variations of internuclear distances of Ha–Hb, Hb–N, and Ha–N are presented each as a function of propagation time based on these three collision energies in Fig. 2. The trajectories are selected in the scattering angle of 22.34°. Figures 2(a), 2(b), and 2(c), especially the first two, show that the attacking atom Ha undergoes several collisions with the target molecule Hb–N and the complexes have relatively long lifetime before breaking up. The long-term survival of the metastable states could allow the system to perform extensive rotations before breaking up, thereby making the products come out in more random directions. So the indirect reactive trajectories, namely “trapped” trajectories, can be observed. Therefore it is no surprise that the forward scattering and backward scattering are observed as can be seen in Fig. 1. The Ha–Hb distance reaches its lowest value before the Ha–N does, that is to say, the attacking Ha atom “hits” firstly on the Hb atom of the target molecule and later migrates to form the HaN product. As a consequence, the reaction takes place by a migration mechanism.[45] Figure 3 shows the internuclear distances of Ha–Hb, Hb–N, and Ha–N each as a function of propagation time based on variation of initial reagent rotational excitations at 30 kcal/mol. It should be noted that the abstraction mechanism could be founded except for j = 0. That is to say, the initial reagent rotational excitation transforms the reaction mechanism from insertion to abstraction. And indirect reactive trajectories (i.e. many intermediate complexes appear) of interest are observed only when j = 6.
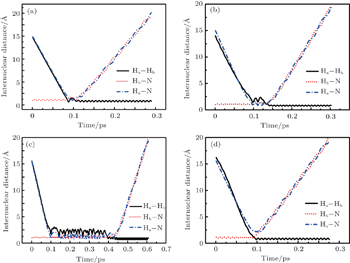
3.2. Energy-dependent k–j′ and k–k′–j′ correlationsIn this section, the energy-dependent behaviors of the angular distributions of P(θr) and P(ϕr) are discussed in detail, with the reactant NH selected at a specific initial state v = 0 and j = 0. The calculated distributions of P(θr) for the product H2 molecule from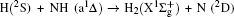 
reaction under the collision energies 10 kcal/mol, 20 kcal/mol, and 30 kcal/mol are plotted in Fig. 4. Each of the distributions of P(θr), describing the k–j′ correlation, has a maximum at a θr angle value of 90° and symmetric with respect to 90°. It can be concluded that j′ is distributed with cylindrical symmetry in the product scattering frame and the direction of j′ is preferentially perpendicular to the k direction. As we can see, the distribution of P(θr) becomes weaker when the collision energy increases from 10 kcal/mol to 20 kcal/mol, while it becomes stronger when the collision energy increases from 20 kcal/mol to 30 kcal/mol. The product rotational alignment parameter 〈P2(j′k)〉 is used to investigate the trend of P(θr) distribution in depth, which are –0.3486, –0.3413, and –0.3683 at these three collision energies respectively (the closer to 0.5 the 〈P2(j′k)〉, the stronger the product alignment is). In the reaction process, the total angular momentum can be conserved as L + j = j′ + L′, where L and j denote the orbital angular momentum and the rotational angular momentum respectively. When the rotational angular momentum of reactants is low (which is the case in H + NH (v = 0, j = 0)) L ≈ j′ + L′. As the collision energy increases, the orbital angular momentum is also improved since the orbital angular momentum can be written as L = bmax(2μ Ecol)1/2 (although bmax decreases with collision energy, the degree of its reduction is incomparable to that of the collision energy increment). As a result, larger parts of L are disposed into j′, which finally induces stronger alignment of j′.
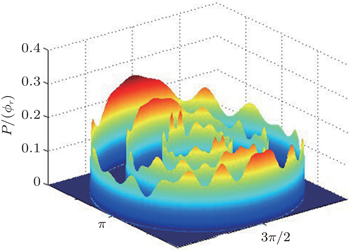
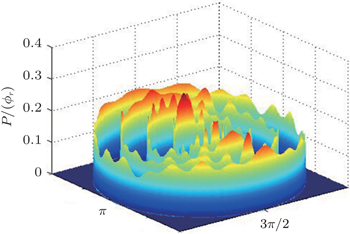
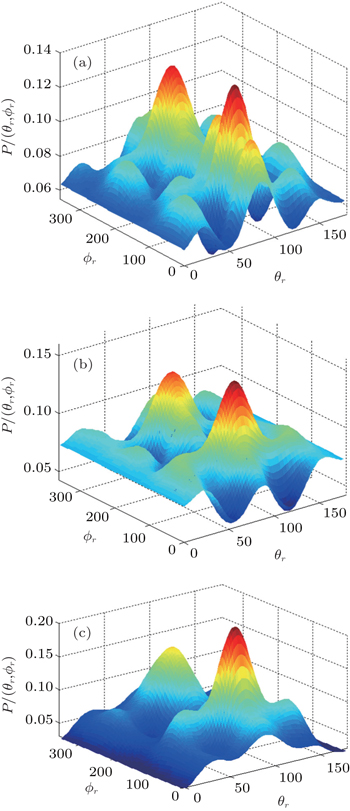
The dihedral angle distribution of P(ϕr) describing the k–k′–j′ correlation is shown in Fig. 5, and it tends to be asymmetric with respect to the k–k′ scattering plane (or about ϕr = 180°) and could be used to reflect the strong polarization of product rotational angular momentum directly. In fact, the peaks in the distribution of P(ϕr) at ϕr angles close to 90° imply a preference for right-handed product rotation while the peaks at ϕr angles close to 270° indicate a preference for left-handed product rotation. The peaks of P(ϕr) appear at ϕr = 90° and ϕr = 270° indicate that the rotational angular momentum vectors of the products are mainly aligned along the y axis of the CM frame. It can be seen that the peaks at ϕr = 90° are stronger than those at ϕr = 270° at these three collision energies, which means that the product rotational angular momentum vector j′ is oriented along the positive direction of the y axis. And the difference in peak between ϕr = 90° and ϕr = 270° increases with the increase of collision energy. It should be noted that the peaks of P(ϕr) distributions at higher collision energies are broader than those at lower collision energies which indicates that the rotation of the product molecule changes from the “in-plane” reaction mechanism into the “outofplane” mechanism. In turn, as depicted in Fig. 5, the P(ϕr) distributions each display a distinct ‘V’-shaped splitting separately around ϕr = 90° and 270° at 10 kcal/mol, which predicts a dynamic enhancement of the degree of orientation along the y axis. A similar splitting was also found in the study of stereodynamics for reaction O + H2.[46] The angular momentum polarization in the form of polar plot of the distribution of P(θr, φr) is also depicted in Fig. 6, which represents the scattering angle average of the full distribution of P(ωt, ωr). The distributions of the P(θr, ϕr) peaks at (π/2, 3π/2) are in good accordance with the distributions of P(θr) and P(ϕr), which indicates that the HH products are preferentially polarized perpendicularly to the scattering plane.
3.3. Rotation-dependent k–j′ and k–k′–j′ correlationsThe effects of the initial rotational excitation of NH on the alignment of product angular momentum j′ in the stereodynamics for the reaction H + NH (v = 0, j = 0, 3, 6, 9) are also investigated. The calculated results of P(θr) distribution for this reaction at 30 kcal/mol collision energy are shown in Fig. 7. It can be seen that the distributions of P(θr) become broader and lower when the reagent rotations are in the cases of j = 3, 6, 9, indicating that the product rotational alignment effect becomes weaker when the reagent is in the excited rotation state. This is also confirmed by the values of the product rotational alignment parameter 〈P2(j′k)〉, which are –0.3683, –0.3460, –0.3546, and –0.350 corresponding to j = 0, 3, 6, and 9, respectively. It should be emphasized that the few peaks of P(θr) distribution close to θr = 0° and 180° appear gradually with the enhancement of the initial rotational excitation of target molecular. It implies that as the initial rotational excitation of target molecular increases, the polarization parallel to the direction of the relative velocity of reactants appears, nothing but the degree of polarization is relatively weak.
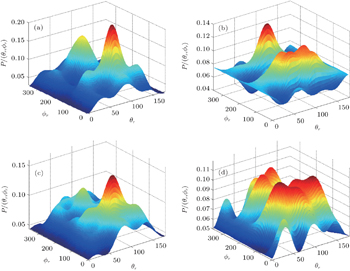
In order to examine the influence of initial rotational state of NH on the orientation of product angular momentum j′, we show the distributions of P(ϕr) in Fig. 8. The dihedral angle distribution of the k–k′–j′ correlation shows that P(ϕr) tends to be asymmetric about ϕr = π, reflecting the strong polarization of angular momentum directly. The product rotational angular momentum is not only aligned along the y axis (i.e. the distributions have peaks at ϕr = π/2 and 3π/2 respectively), but is also oriented along the positive direction of the y axis (i.e., the peaks at ϕr = π/2 are larger than those at ϕr = 3π/2). The P(ϕr) distribution peaking at ϕr angle close to π/2 implies a preference for right-handed HH rotation in planes that are parallel to the scattering plane. It is interesting to find that the reaction is symmetric around the relative velocity vector, while the distribution of P(ϕr) is asymmetric. The various angular distributions of the product reflect the vector correlation containing rich information about the angular momentum polarization. In order to validate the information about the product molecular axis polarization, the P(θr, φr) distributions averaged over all scattering angles for the reactions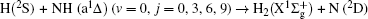 
are shown in Fig. 9. As can be seen, the distributions of P(θr, ϕr) show peaks at θr = 90°, ϕr= 90° and θr = 90°, ϕr = 270°, which are found to be in good accordance with the scenarios for the distributions of P(θr) and P(ϕr) of the HH products. The distributions of P(θr, ϕr) indicate that the products of the reactions are mainly rotated in planes that are parallel to the scattering plane and the products are preferentially polarized perpendicularly to the scattering plane.
4. ConclusionsIn the present work, the energy and rotation-dependent stereodynamics of the reaction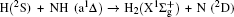 
are studied based on the first excited state DMBE-SEC PES of NH2 using QCT method. A total of 3 × 104 trajectories are run under each initial condition to investigate the effects of collision energy and rotational state of NH radical on the product rotational polarization. With the increase of the collision energy, both forward and backward scatterings become stronger, in which the forward scattering has a bigger magnitude of variation. The influence of collision energy on the k–k′ distribution can be attributed to a purely impulsive effect, and also used to control the reaction mechanism. Whereas with the increase of rotational quantum number, both forward scattering and backward scatterings become lower. It can be explained as the fact that the rotational excitation enlarges the rotational rate of reagent NH in the entrance channel to reduce the probability of collision between incidence H atom and H atom of target molecule. In addition, initial reagent rotational excitation can convert the insertion mechanism into the abstraction mechanism under the condition of high collision energy.
The results of vector correlation show that the product rotational angular momentum j′ is not only aligned, but also oriented along the direction perpendicular to the scattering plane. It is found that the three angle distributions are sensitive to initially collision energy and rotational excitation.
, Yang Yun-Fan1, Yu Yang1, Zhang Yong-Jia1, Ma Feng-Cai1, ‡, 
