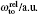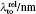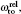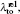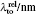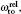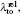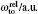Cite this Article
Yu Wei-Wei, Yu Rong-Mei, Cheng Yong-Jun, Zhou Ya-Jun. Tune-out wavelengths for the alkaline-metal atoms. Chinese Physics B, 2016, 25(2): 023101  
Permissions
Tune-out wavelengths for the alkaline-metal atoms
Yu Wei-Wei1, Yu Rong-Mei2, Cheng Yong-Jun3, †, , Zhou Ya-Jun3
School of Physics and Electronic Technology, Liaoning Normal University, Dalian 116029, China
College of Physics and Electronic Engineering, Nanyang Normal University, Nanyang 473061, China
Academy of Fundamental and Interdisciplinary Science, Harbin Institute of Technology, Harbin 150080, China

 

† Corresponding author. E-mail: yongjun.cheng@hit.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11304063 and 11174066) and the Youth Foundation of Liaoning Normal University, China (Grant No. LS2014L002).

Abstract
Abstract

An approximation formula is developed to determine the tune-out wavelengths for the ground states of the alkaline-metal atoms lithium, sodium and cesium from the existing relativistic reduced matrix elements and experimental energies. The first longest tune-out wavelengths for Li, Na, and Cs are 670.971 nm, 589.557 nm, and 880.237 nm, respectively. This is in good agreement with the previous high precise results of 670.971626 nm, 589.5565 nm, and 880.25 nm from the relativistic all-order many-body perturbation theory (RMBPT) calculation [Phys. Rev. A 84 043401 (2011)].

PACS: 31.15.ac;31.15.ap;37.10.De;
Keyword:polarizability;tune-out wavelength;alkaline-metal atom;
1. Introduction

The realization of mixture of trapped ultracold atomic gases in optical lattice is one of the most important improvements in the experimental side in recent years.[1–5] This opens new paths toward the formation of ultracold diatomic molecule and some other targets that the physicists have been seeking for a couple of years.[6–10] The atom can be trapped in the optical lattice by the optical dipole force and will experience an energy shift due to the ac stark effect. Both effects are proportional to the dynamic polarizability of the atom and can be cancelled at certain wavelength where the dynamic polarizability of the atom goes to zero. This means that the atom is unaffected by the presence of the electromagnetic field and also can be released from the trap simply while the other atom in the mixture are still strongly trapped. Such wavelength is termed as the “tune-out wavelength”[11,12] and has attracted much attention recently.

A number of experimental measurements on the determination of the tune-out wavelengths have been performed in the past few years. Since the measurement is a null experiment, it is not subject to the strength of an electric field or the intensity of a laser field. The tune-out wavelengths for the Rb and K atoms have been measured by different groups.[13–15] Holmgren et al.[14] measured the longest tune-out wavelength of potassium to an uncertainty of 1.5 pm by using an atom interfermeter. This is more accurate than the uncertainty of 3 pm which is performed by using state-of-the-art atomic theory.[12] Some tune-out wavelengths for rubidium have also been measured through the diffraction of a Bose-Einstein condensate off a sequence of standing wave pulses.[13] On the theoretical side, the most reliable prediction of the tune-out wavelength for the alkaline-metal atoms is the relativistic all-order many-body perturbation theory (RMBPT) calculation.[12]

In this paper, we present an estimate of the longest tune-out wavelengths for the alkaline-metal atoms: lithium, sodium, and cesium using a formula which is obtained through the analysis of an exact non-relativistic calculation of the tune-out wavelengths for lithium and sodium. This non-relativistic calculation of the tune-out wavelengths are computed using the configuration interaction plus core polarization (CICP) method in which a semiempirical potential is adopted to describe the polarization effect between the core and valence electrons. This method has been successfully applied to the description of many one- and two-electron atoms.[16–22] The detailed analysis of the exact CICP calculation shows that the tune-out wavelengths are determined by explicit calculation of the dynamic polarizability at a series of ω values and they all tend to be close to the transition energies of np states for the alkaline-metal atoms. The fine structure split is not considered in CICP calculation and thus it cannot be used to give the accurate values of tune-out wavelengths. However an approximation formula can be built since that the CICP calculation shows that the values of the tune-out wavelengths are mostly determined by the data of only a few transitions. Using this formula, one can use the existing experimental and theoretical transition information to predict the tune-out wavelengths for the alkaline-metal atom.

The present relativistic estimate of the three longest tune-out wavelengths for lithium and four longest wavelengths for sodium are given in this paper along with the related non-relativistic calculation as a validity. Due to the strong relativistic effect, we do not give the CICP calculation about Cs, but only present the relativistic estimates of the five longest tune-out wavelengths in Section 3.

2. CICP calculations
2.1. Non-relativistic model

The details of the non-relativistic CICP method have been given elsewhere[17,18] and here we only briefly outline this method. The CICP method was a frozen-core procedure. The core electron was represented by a Hartree–Fock wavefunction that was calculated exactly using Slater-type orbitals (STOs). The effective Hamiltonian for the valence electrons was essentially a fixed core Hamiltonian with the addition of semiempirical potentials to allow for the polarization interaction with the core.[23] The direct and exchange interactions of the valence with the Hartree–Fock core electrons were computed without approximation. The semiempirical polarization potential was tuned so that they reproduced the binding energies of the ns ground state, the np and nd excited states.[23] The effective Hamiltonian was diagonalized in a very large orbital basis of Laguerre-type orbitals for each l value due to the superior linear dependence properties. The semiempirical core polarization potential Vp has the functional form:

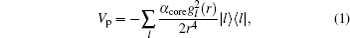
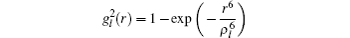
where the factor αcore is the static dipole polarizability of the core,

is a cutoff function, and ρl is the cutoff parameter.

A good test of the CICP method comes from the tabulation of the energy in Table 1. The energy levels of ground state and some of lower energy excited states for Li and Na are given and compared with experiment. The experimental one-electron binding energies were determined from the NIST tabulation.[24] The agreement with experiment for the lowest states of each symmetry is excellent since the polarization cutoff parameters are tuned to reproduce the experimental binding energy of these states. The agreement level of the excited states is also good which indicates the validity of the CICP method.

Table 1.

Theoretical and experimental energy levels (in Hartree unit) for some of the low-lying states of alkaline-metal atoms. The experimental data were taken from the NIST tabulation.[24] The experimental energies for the doublet states are averages with the usual (2J + 1) weighting factors.

.

The dynamic polarizability is defined as

where f0n is the oscillator strength for the dipole transition from the ground state and ε0n is the transition energy. When the frequency goes to zero, the polarizability is the static polarizability. As another validation of the CICP method, the static dipole polarizabilities for the ground states of Li, Na and Cs produced in the CICP calculation are listed in Table 2 and compared with the theoretical values from Refs. [25], [26], [27], [28] and the experimental results.[29–32] All the static polarizabilities are computed using experimental energy differences for the lowest energy excited states and the core contributions are also added. The value of 403.6(81) a.u. (The unit a.u. is short for atomic unit) in Cs is weighted average of experimental data from Refs. [31] and [32]. The CICP static polarizabilities are in good agreement with the experimental measurement except for Cs which is as expected since the relativistic effect is important for Cs.

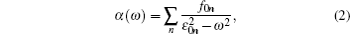
Table 2.

Static dipole polarizability for the ground states of the lithium, sodium and cesium atoms. Numbers in brackets represent the uncertainties in the last digits. All values are in atomic units.

.

Table 3 shows the four tune-out wavelengths for lithium and sodium from the non-relativistic CICP calculation. The contributions to the polarizability from individual transitions are also listed. One can find that the tune-out wavelengths all tend to occur close to the wavelengths for excitation of the np excited states. Taking lithium as an example, the first tune-out wavelength is located between the 2s–2p resonant transition and the 2s–3p excitation energies and mainly dominated by these two terms. The 3p term has the opposite sign and cancels out most of the 2p contribution. The remainder and core terms make a small contribution to the total polarizability. In other situations, the tune-out wavelengths all occur just below the excitation energies of the 4p, 5p, and 6p states. This is due to the fact that the polarizability is proportional to the square of the reduced matrix elements. The magnitude of the 2s–2p matrix element is more than one order larger than the 2s–np (n = 4,5,6) matrix element, then these tune-out wavelengths must be very close the corresponding 2s–np excitation energies so that the contribution to the total polarizability from the 2s–np term can cancel the contribution from 2s–2p term. From Table 3, one can also find another point that the remainder polarizability varies relatively slowly with wavelength in the vicinity of the tune-out wavelength. The feature is common to the sodium atom.

Table 3.

Breakdown of contributions to the static polarizability and the dynamic polarizabilities at different tune-out wavelengths, λto, for lithium and sodium. The adopted experimental transition energies are also listed.

.
2.2. Approximation formula and its accurate level

As can be seen from Table 3, the tune-out wavelengths for the alkaline-metal arise as a result of the interference between the dynamic polarizabilities arising from a large background polarizability and a transition near the tune-out wavelength. The polarizability near the tune-out wavelength can be modeled as

where α0 is the background polarizability arising from all transitions except the transition most close to the tune-out wavelength. Then the background polarizability α0 is dominated by contribution from the resonant transition and can be represented as

where αrest is the rest polarizability, only accounts for a few percent of the resonance transition, and varies slowly with the tune-out frequency. Therefore, we assume that αrest has the same value at ω = 0 and ωto. Then the value of αrest can be calculated as

where αd is the static polarizability of the ground states. fresonant, f, ΔEresonant, and ΔE are the oscillator strengths and transition energies of the resonant transition and the transition near the tune-out wavelength respectively. Using Eq. (3), one can give a non-relativistic estimate of the tune-out wavelengths. The detailed calculations employing the approximation formula are listed in Tables 4 and 5. In our calculations, the transition energies are taken from the NIST tabulation[24] and oscillator strengths come from the CICP calculation. Table 4 shows that the tune-out wavelengths for the lithium atom are 324.167 nm, 274.889 nm, 256.709 nm, and 247.855 nm respectively and the differences with the values obtained from the exact CICP calculation are only 0.02 nm, 0.024 nm, 0.009 nm, and 0.001 nm respectively. Similarly, the tune-out wavelengths for sodium are listed in Table 5. The four tune-out wavelengths for sodium are 331.875 nm, 285.587 nm, 268.179 nm, and 259.497 nm. The differences with the exact CICP calculations are 0.006 nm, 0.011 nm, 0.004 nm, and 0.002 nm. There is a general degree of consistency between the estimated tune-out wavelengths and the exact CICP calculations.

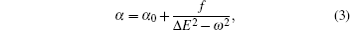
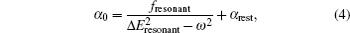
Table 4.

Tune-out frequencies, ωto, and wavelengths, λto, for the four tune-out wavelengths of Li from a non-relativistic CICP calculation. The contribution to the polarizability at the tune-out frequency due to the resonance transition is given. The transition energies are taken from the NIST tabulation.[24] The adopted CICP values of Sresonant, fresonant, and αd are 16.5124, 0.747538, and 164.205 a.u. respectively.

.
Table 5.

Tune-out frequencies, ωto, and wavelengths, λto, for the four tune-out wavelengths of Na from a non-relativistic CICP calculation. The contribution to the polarizability at the tune-out frequency due to the resonance transition is given. The transition energies are taken from the NIST tabulation.[24] The adopted CICP values of Sresonant, fresonant, and αd are 18.6619, 0.961838, and 162.801 a.u. respectively.

.
3. Relativistic estimation for Li, Na, and Cs
3.1. Model for the relativistic formula

Based on the analysis of the non-relativistic calculation and the fact that the fine structure split of the energy levels is not considered, the present non-relativistic calculational methodology cannot be applied to the determination of the accurate tune-out wavelengths. However, equation (3) can be used to make an initial estimate of their longest tune-out wavelengths from the existing experimental energies and the previous relativistic reduced matrix elements. Considering the fine structure split of the energy levels, equation (3) is changed into the following form

For the first longest tune-out wavelength of lithium, the dynamic polarizability is dominated by the 2s→ 2p1/2 resonant transition and the transition 2s→ 2p3/2 that is most close to the tune-out wavelength,

while for other tune-out wavelengths,

for n ≥ 3.

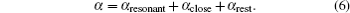
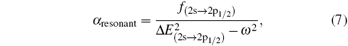
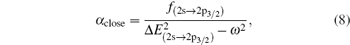
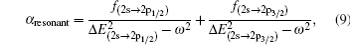
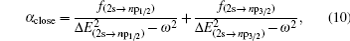
Similar form is adopted for the sodium atom with the 2pj state replaced by the 3pj state, and for cesium with the 2pj state replaced by the 6pj state.

3.2. Estimated analysis

All the fundamental information adopted here to make an estimate of the tune-out wavelength for lithium, sodium and cesium is listed in Table 6. The oscillator strengths used here are calculated from the CCSD(T) matrix elements,[33] SD matrix elements,[25] and experimental transition energies of NIST tabulation.[24] The longest tune-out wavelengths for lithium and sodium with the CCSD(T) matrix elements and the experimental energies[24] are listed in Tables 7 and 8, respectively. The three longest tune-out wavelengths for lithium are 670.971 nm, 324.161 nm, and 274.883 nm. Compared with the all-order RMBPT calculation,[12] the differences are 6.2 × 10−4 nm, 1.9 × 10−2 nm, and 2.8 × 10−2 nm. The predicted four longest tune-out wavelengths for sodium are 589.557 nm, 331.839 nm, 330.372 nm, and 285.581 nm. One can note that our values for the first longest tune-out wavelengths compared with the Arora et al.[12] calculations achieve an accuracy of 0.001-nm level.

Table 6.

The experimental transition energies[24] and oscillator strengths used in the calculation. The oscillator strengths are calculated using the reduced matrix elements from the CCSD(T)[33] and SD[25] calculation.

.
Table 7.

Tune-out frequencies, and wavelengths, for the longest tune-out wavelengths of Li. The contributions to the polarizability at the tune-out frequency due to the resonance transition, the close transition and the rest transition are given. The adopted value of αd is 164.2 a.u.[29].

.
Table 8.

Tune-out frequencies, and wavelengths, for the longest tune-out wavelengths of Na. The contributions to the polarizability at the tune-out frequency due to the resonance transition, the close transition and the rest transition are given. The adopted value of αd is 162.7 a.u.[30].

.

The element Cs has been the subject of various theoretical calculations and experiments in atomic clock research.[34,35] The value of tune-out wavelength for Cs could be very useful for experimentalist. The measurements of tune-out wavelengths are also used to test the precision of the excited-state matrix elements which are difficult to measure or calculate. Due to the large correlation corrections, the transition matrix elements are hard to calculate accurately. The measurement of 6s–7pj transition in Cs has been performed in Ref. [36]. The longest tune-out wavelengths and the contributions to the polarizability at the tune-out frequency for Cs are given in Table 9. The five longest tune-out wavelengths for Cs are 880.237 nm, 460.444 nm, 457.411 nm, 391.435 nm, and 388.637 nm, respectively. There is a reasonable consistency compared with the RMBPT results.[12]

Table 9.

Tune-out frequencies, and wavelengths, for the longest tune-out wavelengths of Cs. The contributions to the polarizability at the tune-out frequency due to the resonance transition, the close transition and the rest transition are given. The adopted value of αd = 403.6 a.u. is weighted average of experimental data from Refs. [31] and [32].

.
3.3. Uncertainties

An estimate of the uncertainties for the first longest tune-out wavelength of Li, Na, and Cs can be made through Eq. (3) and by examination of the difference of polarizabilities and transition matrix elements between existing experiment and theoretical data. We set α = 0, then equation (3) is given as

Then equation (11) can be used for an uncertainty analysis. Setting Xshift = f/(2α0ΔE2), one has

At the present level of accuracy, the uncertainty in the transition energy does not have to be considered. Xshift makes an estimate of the relative difference between the transition frequency and tune-out frequency. The uncertainty in Xshift only considers the uncertainties in oscillator strengths and background polarizabilities, one can have

Then the uncertainty in tune-out wavelength can be obtained

The constant β = 137.035999 a.u. is the velocity of light in atomic units. The uncertainties of the oscillator strengths and polarizabilities are made by examination of the adopted data and existing experimental and theoretical information.

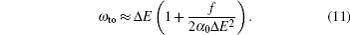
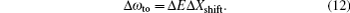
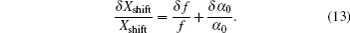
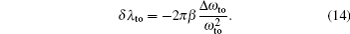
Another useful parameter for the measurement of tune-out wavelength is the energy window Δω. We suppose that the condition for determination of the tune-out wavelength is that the polarizability be set to zero with an uncertainty of ±0.1 a.u. The photon energy range at which the dynamic polarizability is 0 ± 0.1 a.u. is termed as the energy window Δω,

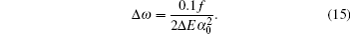
The energy window for Li is Δω = 1.95 × 10−14 a.u. and Xshift is 1.51 × 10−5. The uncertainty of the first longest tune-out wavelength for lithium is δλto = 4.74 × 10−6 nm. Similarly, for sodium, the energy window is Δω = 4.35 × 10−11 a.u., Xshift is 6.76 × 10−4, and the uncertainty of the first longest tune-out wavelength is δλto = 0.0937 nm. For Cs, the energy window is Δω = 2.80 × 10−8 a.u., Xshift is 0.0312, and the uncertainty of the first longest tune-out wavelength is δλto = 0.388 nm. The energy windows for lithium and sodium are too narrow and difficult to achieve with existing technology, while the energy window for cesium is relatively larger and more feasible.

Using a similar method, we could also obtain the uncertainties for other longest tune-out wavelengths. The uncertainties for the second and third longest tune-out wavelengths of lithium are 0.013 nm and 0.009 nm, respectively. The corresponding energy windows are 1.49 × 10−6 a.u. and 2.71 × 10−6 a.u. For sodium, the uncertainties for the second, the third, and the fourth tune-out wavelengths are 0.063 nm, 0.0001 nm, and 0.013 nm. The corresponding energy windows are 1.74 × 10−6 a.u., 6.26 × 10−10 a.u., and 5.22 × 10−7 a.u. For the cesium atom, the uncertainties for the second and third longest wavelengths are 0.559 nm and 0.748 nm which are relatively larger since the matrix elements are more difficult to calculate precisely. The corresponding energy windows are 7.49 × 10−8 a.u. and 1.16 × 10−7 a.u.

4. Conclusion

The longest tune-out wavelengths for the lithium, sodium and cesium atoms are computed by an approximation formula. The accuracy of the calculation is tested by comparing with the all-order RMBPT calculation.[12] The first longest tune-out wavelengths for Li, Na, and Cs are 670.971 nm, 589.557 nm, and 880.237 nm, respectively. The agreement of the first longest tune-out wavelength is at the 0.001-nm level. Some other longest tune-out wavelengths are also calculated, and there is a reasonable agreement with the RMBPT results.[12] The wavelengths near some resonances which are in the ultraviolet are not calculated, since they are difficultly detected in most laboratories. The uncertainties of the predicted tune-out wavelengths are derived from the difference among the existing transition matrix elements. An parameter termed as the energy window of tune-out wavelength is developed as an indication of the technology required to measure these wavelengths. The longest tune-out wavelengths for lithium and sodium are difficult to measure with existing technology due to their too narrow energy windows while the first three tune-out wavelengths for atomic cesium and the tune-out wavelengths for lithium positioned at 324.161 nm and 274.883 nm and for sodium positioned at 331.839 nm are more feasible choices.

Reference
1Truscott A GStrecker K EMcAlexander W IPartridge G BHulet R G 2001 Science 291 2570
2Schreck FKhaykovich LCorwin K LFerrari GBourdel TCubizolles JSalomon C 2001 Phys. Rev. Lett. 87 080403
3Modugno GFerrari GRoati GBrecha R JSimoni AInguscio M 2001 Science 294 1320
4Ivanov V VKhramov AHansen A HDowd W HMuenchow FJamison A OGupta S2011Phys. Rev. Lett.106153201
5Jia Y FGuo H MQin J HChen Z YFeng S P 2013 Chin. Phys. B 22 090308
6Papp S BWieman C E 2006 Phys. Rev. Lett. 97 180404
7Ospelkaus COspelkaus SHumbert LErnst PSengstock KBongs K 2006 Phys. Rev. Lett. 97 120402
8Ospelkaus COspelkaus S 2008 J. Phys. B: At. Mol. Opt. Phys. 41 203001
9Ni K KOspelkaus Sde Miranda M H GPeér ANeyenhuis BZirbel J JKotochigova SJulienne P SJin D SYe J 2008 Science 322 231
10Voigt A CTaglieber MCosta LAoki TWieser WHänsch T WDieckmann K 2009 Phys. Rev. Lett. 102 020405
11LeBlanc L JThywissen J H 2007 Phys. Rev. A 75 053612
12Arora BSafronova M SClark C W 2011 Phys. Rev. A 84 043401
13Herold C DVaidya V DLi XRolston S LPorto J VSafronova M S 2012 Phys. Rev. Lett. 109 243003
14Holmgren W FTrubko RHromada ICronin A D 2012 Phys. Rev. Lett. 109 243004
15Trubko RGreenberg JGermaine M T SGregoire M DHolmgren W FHromada ICronin A D2015Phys. Rev. Lett.114140404
16Mitroy JGriffin D CNorcross D WPindzola M S 1988 Phys. Rev. A 38 3339
17Mitroy JBromley M W J 2003 Phys. Rev. A 68 052714
18Mitroy JSafronova M S 2009 Phys. Rev. A 79 012513
19Mitroy JZhang J YBromley M W JRollin K G 2009 Eur. Phys. J. D 53 15
20Jiang JTang L YMitroy J 2013 Phys. Rev. A 87 032518
21Cheng Y JJiang JMitroy J 2013 Phys. Rev. A 88 022511
22Yu W WYu R MCheng Y J 2015 Chin. Phys. Lett. 32 123102
23Mitroy JBromley M W J 2003 Phys. Rev. A 68 035201
24Kramida ARalchenko YReader JNIST ASD Team2012NIST Atomic Spectra Database(Version 5.00) http://physics.nist.gov/asd
25Safronova M SJohnson W RDerevianko A 1999 Phys. Rev. A 60 4476
26Kaur KKaur JArora B 2014 Phys. Rev. B 90 245405
27Tang Y BLi C BQiao H X 2014 Chin. Phys. B 23 063101
28Marinescu MSadeghpour H RDalgarno A 1994 Phys. Rev. A 49 982
29Miffre AJacquest MBuchner MTrenec GVigue J 2006 Eur. Phys. J. D 38 353
30Ekstrom C RSchmiedmayer JChapman M SHammond T DPritchard D E 1995 Phys. Rev. A 51 3883
31Hall W DZorn J C 1974 Phys. Rev. A 10 1141
32Molof R WSchwartz H LMiller T MBederson B 1974 Phys. Rev. A 10 1131
33Sahoo B KArora B 2013 Phys. Rev. A 87 023402
34Oblak DPetrov P GAlzar C L Get al. 2005 Phys. Rev. A 71 043807
35Rosenbusch PGhezali SDzuba V AFlambaum V VBeloy KDerevianko A 2009 Phys. Rev. A 79 013404
36Vasilyev A ASavukov I MSafronova M SBerry H G 2002 Phys. Rev. A 66 020101