Cite this Article
Zhou Lan, Sheng Yu-Bo. Efficient entanglement concentration for arbitrary less-entangled NOON state assisted by single photons. Chinese Physics B, 2016, 25(2): 020308  
Permissions
Efficient entanglement concentration for arbitrary less-entangled NOON state assisted by single photons
Zhou Lan1, 2, Sheng Yu-Bo2, 3, †,
College of Mathematics and Physics, Nanjing University of Posts and Telecommunications, Nanjing 210003, Chinavglue
Key Laboratory of Broadband Wireless Communication and Sensor Network Technology, Ministry of Education, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
Institute of Signal Processing Transmission, Nanjing University of Posts and Telecommunications, Nanjing 210003, China

 

† Corresponding author. E-mail: shengyb@njupt.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11474168 and 61401222), the Qing Lan Project of Jiangsu Province of China, the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20151502), and the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Abstract
Abstract

We put forward two efficient entanglement concentration protocols (ECPs) for arbitrary less-entangled NOON state. Both ECPs only require one pair of less-entangled NOON state and an auxiliary photon. In the first ECP, the auxiliary photon is shared by two parties, while in the second ECP, the auxiliary photon is only possessed by one party, which can increase the practical success probability by avoiding the transmission loss and simplify the operations. Moreover, both ECPs can be used repeatedly to get a high success probability. Based on the above features, our two ECPs, especially the second one, may be useful in the quantum information processing.

PACS: 03.67.Dd;03.67.Hk;03.65.Ud;
Keyword:quantum communication;NOON state;entanglement concentration;cross-Kerr nonlinearity;
1. Introduction

Entanglement plays a significant role in the quantum information field. For example, quantum teleportation,[1,2] quantum densecoding,[3] quantum secret sharing,[4] quantum computation,[5–7] communication,[8–10] protocols[11–22] all require entanglement to set up the quantum entanglement channels. Recently, a special quantum state, which is the so-called NOON state, has attracted much attention.[23–29] The NOON state can be written with the form of

where all the N particles are in the spatial mode a and none are in the spatial mode b, plus none in the mode a and all in the mode b. The NOON state has provided many important applications. For example, it has been proved that the NOON state can serve as an important resource for Heisenberg-limited metrology and quantum lithography, where it has sensitivity for optical interferometry and can approach the Heisenberg limit of 1/N.[30–32] Meanwhile, the NOON state also shows the de Broglie wavelength of λ/N for N-photon interference.[26,33–35] It is worth noting that the power of the NOON state lies in its entanglement. In all applications, the ideal NOON state should be the maximally entangled NOON state as in Eq. (1). However, in practical application process, since the decoherence is unavoidable during the storage and transmission of particles over noisy channels, the maximally entangled NOON state can be easily degraded. The noise may make the maximally entangled NOON state degrade to the pure less-entangled NOON state, which will limit its practical applications largely. Therefore, we need to recover it into the maximally entangled NOON state prior to the practical applications.

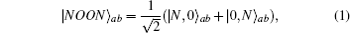
The method for recovering the pure less-entangled state into the maximally entangled state is called the entanglement concentration. In 1996, Bennett et al. proposed the first entanglement concentration protocol (ECP), which is known as the Schmidt projection method.[36] Since then, various interesting ECPs have been put forward, successively.[37–78] For example, in 1999, Bose et al. proposed an ECP based on entanglement swapping,[37] which was later improved by Shi et al.[38] In 2001, Zhao et al. and Yamamoto et al. proposed two similar concentration protocols based on polarizing beam splitters (PBSs) independently.[39,40] In 2008, Sheng et al. developed their protocols with the help of the cross-Kerr nonlinearity.[41] So far, most of the ECPs are focused on the two-particle entanglement, especially the encoding system in the polarization degree of freedom of the optical system. They cannot deal with the less-entangled NOON state. Recently, we have proposed an ECP for the less-entangled NOON state.[44] In the protocol, two pairs of less-entangled NOON states are required. After performing this ECP, one pair of maximally entangled NOON state can be obtained. As the NOON state is precious, this protocol is not optimal.

In the present paper, we put forward two efficient ECPs for arbitrary less-entangled NOON state. Different from the previous ECP,[44] both of our ECPs only require one pair of less-entangled NOON state and a single auxiliary photon to complete the concentration task and can reach the same success probability as Ref. [44]. In the two ECPs, we adopt the cross-Kerr nonlinearity to construct the quantum nondemolition detection (QND) gate, which means the obtained maximally entangled NOON state can be kept for other applications. Moreover, both the ECPs can be used repeatedly to get a high success probability. The second ECP is more optimal than the first one, for it only requires the local single auxiliary photon, which can effectively avoid the photon loss during the transmission process. Moreover, one party can perform the whole task which can simplify the practical experiment largely.

This paper is organized as follows: In Sections 2 and 3, we explain the basic principles of the first and the second ECPs, respectively. Some discussions are made in Section 4, and a summary is given in the last section.

2. The first concentration protocol for the N-photon NOON state

The cross-Kerr nonlinearity is the key element of both ECPs. Therefore, we would like to make a brief introduction about it first. The cross-Kerr nonlinearity has been widely used in the quantum information field. It has played an important role in the construction of CNOT gate,[79,80] Bell-state analysis,[81,82] and so on.[83–92] In particular, the cross-Kerr nonlinearity is a powerful tool in the construction of the QND gate, which is widely used in the quantum entanglement concentration.[41–43,55,57] The cross-Kerr nonlinearity can be described by its Hamiltonian as

where ħχ is the coupling strength of the nonlinearity, which depends on the cross-Kerr material.[79,80,93] n̂a and n̂b are the photon number operators for the spatial modes a and b, respectively. During the cross-Kerr interaction, a laser pulse in the coherent state |α〉 interacts with photons through a proper cross-Kerr material. If the single photon is presented, it can induce a phase shift θ to the coherent state. The cross-Kerr interaction can be described as

Here, |0〉 and |1〉 mean no photon and one photon, respectively. θ = χt, and t means the interaction time for the signal with the nonlinear material. According to Eq. (3), the phase shift of the coherent state is directly proportional to the number of photons. Therefore, by measuring the phase shift of the coherent state, we can check the photon number without destroying the photons.

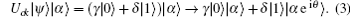
Now, we start to explain the first ECP for arbitrary less-entangled NOON state. The principle of the ECP is shown in Fig. 1. We suppose that Alice (A) and Bob (B) share a less-entangled N-photon NOON state |ϕ〉a1b1 in the spatial modes a1 and b1, which is generated by the photon source S1. |ϕ〉a1b1 can be written as

Here, α and β are the entanglement coefficients of the NOON state, where |α|2 + |β|2 = 1, and α ≠ β.

Fig. 1. A schematic diagram of the first ECP. The single photons in the spatial modes b1 and b2 can make the coherent state pick up the phase shifts of −θ/N and θ, respectively. BS means 50:50 beam splitter. After the BS, the output photons in the spatial modes d1 and d2 will be detected by the single-photon detectors D1 and D2, respectively.

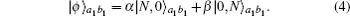
A single-photon entanglement source S2 emits an auxiliary photon and sends it to Alice and Bob in the spatial modes a2 and b2, which creates a single-photon entangled state of the form

Here, for ensuring the coefficients of the auxiliary photon, we need to know the initial coefficients of the less-entangled NOON state, α and β, which are not difficult to know by measuring a sufficient amount of the sample of entangled NOON state.

In this way, the whole (N + 1)-photon system can be described as

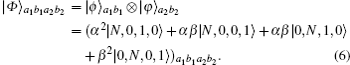
According to Fig. 1, Bob makes the photons in the spatial modes b1 and b2 pass through two cross-Kerr nonlinearities, respectively. Then, the (N + 1)-photon system combined with the coherent state can evolve to

From the above Eq. (7), the items |N,0,0,1〉a1b1a2b2 and |0,N,1,0〉a1b1a2b2 can make the coherent state pick up the phase shifts of θ and −θ, respectively, while the other two items make the coherent state pick up no phase shift. As ±θ is indistinguishable in the homodyne measurement, Bob selects the items corresponding to the phase shift of ±θ, and discards the other items. Under this case, the state in Eq. (6) will collapse to

with the success probability of 2|αβ|2.

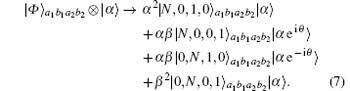
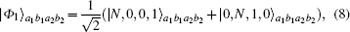
Then, Alice and Bob make the photons in the modes a2 and b2 pass through the 50:50 BS, which makes

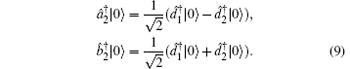
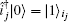
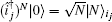
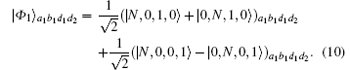
Here, aj, bj, and dj (j = 1,2) are the creation operators for the spatial mode aj, bj, and dj, respectively. The creation operators obey the rules that and . After the BS, |Φ1〉a1b1a2b2 can ultimately evolve to

Finally, the output photons in the spatial modes d1 and d2 are detected by the single-photon detectors D1 and D2, respectively. If the detector D1 fires, the state in Eq. (10) will collapse to

while if the detector D2 fires, the state in Eq. (10) will collapse to

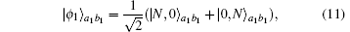
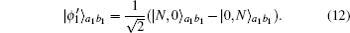
Both |ϕ1〉a1b1 and are the maximally entangled N-photon NOON states and there is only a phase difference between them. can be converted to |ϕ1〉a1b1 by the phase flip operation. So far, the first concentration protocol is completed. In the protocol, with the help of the QND gate constructed by the cross-Kerr nonlinearity, Alice and Bob can distill the maximally entangled N-photon NOON state with the success probability P = 2|αβ|2.

Moreover, we will prove that the ECP can be reused to further concentrate the discarded items. In the first ECP, the discarded items which make the coherent state pick up no phase shift can be written as

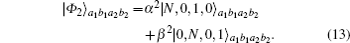
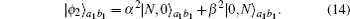
Alice and Bob also make the photons in the spatial modes a2 and b2 pass through the BS, and detect the output photons in the d1 and d2 modes. After that, they can finally obtain

It can be found that |ϕ2〉a1b1 has a similar form to the initial NOON state in Eq. (4), that is to say, |ϕ2〉a1b1 is a new less-entangled N-photon NOON state and can be reconcentrated for the next round. In the second concentration round, the single photon source S2 creates an auxiliary single-photon entangled state with the form of

Following the operations mentioned above, Bob makes the photons in the spatial modes b1 and b2 pass through the QND, and the whole (N + 1)-photon system combined with the coherent state can be described as

Then, Bob still selects the items which make the coherent state pick up the phase shift of ±θ, and the state in Eq. (16) can collapse to the state in Eq. (8). For obtaining the maximally entangled N-photon NOON state, Alice and Bob also make the photons in the spatial modes a2 and b2 pass through the BS, and detect the photons in the d1 and d2 modes. In this way, the state in Eq. (8) can evolve to the maximally entangled N-photon NOON state. It can be calculated that in the second concentration round, the success probability is

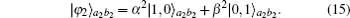
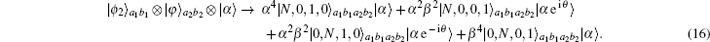
Similarly, by making the discarded items in the second concentration round pass through the BS and detect the output photons, the parties can ultimately obtain a new less-entangled NOON state as

which can be concentrated in the third round. Therefore, by providing an auxiliary single-photon entangled state as

in the k-th concentration round (k = 1, 2, 3, …), our ECP can be used repeatedly to further concentrate the less-entangled NOON state.

3. The second ECP of the N-photon NOON state

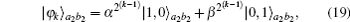
The schematic diagram of our second ECP is shown in Fig. 2. We also suppose that Alice and Bob share a less-entangled N-photon NOON state |ϕ〉a1b1 with the form of Eq. (4), which is generated by S1. Here, the single-photon source S2 emits an auxiliary photon and only sends it to Bob in the spatial mode b2. Bob makes this auxiliary photon pass through a variable beam splitter (VBS) with the transmittance of t, which can create a single-photon entangled state between the spatial modes c1 and c2 with the form of

Here, we should point out that the input mode b2 will couple with the vacuum state in the another input mode of the VBS. However, the vacuum state does not affect the final result, which can be omitted for simplicity. In this way, the whole (N + 1)-photon system can be descried as

Fig. 2. A schematic diagram of our second ECP. The single photon source S2 emits an auxiliary photon and only sends it to Bob. The VBS represents the variable beam splitter with the transmittance of t.

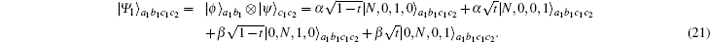
Bob makes the photons in the spatial mode b1 and c1 pass through the QND gate, and the whole (N + 1)-photon system combined with the coherent state can evolve to

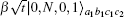
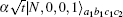
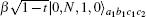
It can be seen that the items and make the coherent state pick up the phase shift of ±θ, while both the items and make it pick up 0 phase shift. Bob selects the items corresponding to the phase shift ±θ and discards the other items. Then, |Ψ〉a1b1c1c2 in Eq. (21) will collapse to

with the success probability of P′ = |α|2(1−t) + |β|2t.

Then, Bob makes the photons in the spatial modes c1 and c2 pass through the 50:50 BS, which makes

After the BS, |Ψ2〉a1b1c1c2 can evolve to

Finally, the output photons in the e1 and e2 modes are detected by the detectors D1 and D2, respectively. It is obvious that if D1 fires, |Ψ3〉a1b1e1e2 will collapse to

while if D2 fires, |Ψ3〉a1b1e1e2 will collapse to

If Bob gets |ψ2〉a1b1 in Eq. (26), he can convert it to |ψ1〉a1b1 with the phase shift operation. According to Eq. (25), if we can find a suitable VBS with the transmittance of t = α2, equation (25) can evolve to Eq. (11), which describes the maximally entangled NOON state. Under the case of t = α2, the success probability of this ECP is

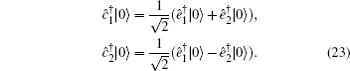
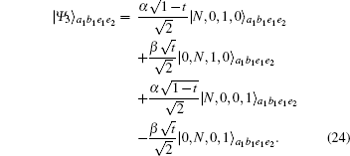
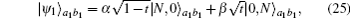
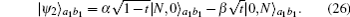
Moreover, we can also prove that the second ECP can be used repeatedly. When t = α2, the discarded items in the first concentration round can be written as

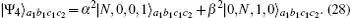
Bob still makes the photons in the spatial modes c1 and c2 pass through the BS, and detects the photons in the e1 and e2 modes. |Ψ4〉a1b1c1c2 can finally evolve to the state in Eq. (14), which is a new less entangled N-photon NOON state and can be reconcentrated in the next concentration round.

In the second concentration round, the single photon source S2 provides a new auxiliary single photon to Bob. Bob makes it pass through another VBS with the transmittance of t2, where the subscript “2” means in the second concentration round. A new single-photon entangled state with the similar form of Eq. (20) can be created. Bob makes the photons in the spatial modes b1 and c1 pass through the QND gate. Then, the whole (N + 1)-photon system combined with the coherent state can be written as

Bob still selects the items which make the coherent state pick up the phase shift of ±θ, and the above state can evolve to

with the success probability of |α|4(1−t2) + |β|4t2.

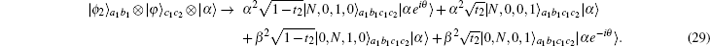
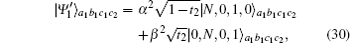
Next, Bob makes the photons in the spatial modes c1 and c2 pass through the BS, and detects the output photons. In this way, will finally evolve to

If we can find a suitable VBS with the form

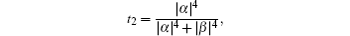
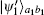
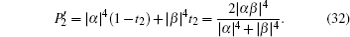
in Eq. (31) can evolve to the state of Eq. (11). That is to say, the new less-entangled NOON state can be ultimately recovered to the maximally entangled NOON state with the probability

where the subscript “2” means in the second concentration round.

Similarly, by making the discarded items in the second concentration round pass through the BS, the discarded items can also evolve to a new less-entangled NOON state, which can be reconcentrated in the next round. Therefore, by choosing the suitable VBSs with the transmittance

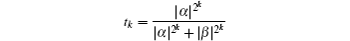
where the subscript “k” means the iteration time, the second ECP can also be used repeatedly to distill the maximally entangled NOON state.

Finally, we would like to calculate the total success probability of these two ECPs. According to the description mentioned above, both ECPs have the same success probability. In each concentration round, the success probability can be written as

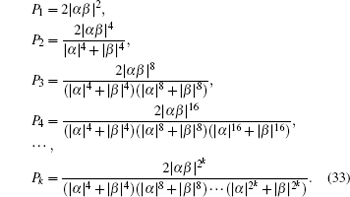
In theory, the ECPs can be reused indefinitely, and the total success probability equals the sum of the probability in each concentration round, which can be described as

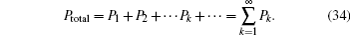
It can be found that if the initial entangled state is the maximally entangled NOON state, where 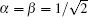, the probability Ptotal = 1/2 + 1/4 + 1/8 + ··· + 1/2k + ··· = 1, while if α ≠ β, the Ptotal <1. Figure 3 shows the value of Ptotal as a function of the entanglement coefficient α, under the iteration number k = 1, 3, 5, respectively. It can be found that Ptotal largely depends on the initial entanglement state. The higher initial entanglement leads to the greater Ptotal. Meanwhile, increasing the iteration number can largely increase the Ptotal. For example, when , Ptotal ≈ 0.500 under k = 1, while Ptotal ≈ 0.968 under k = 5.

Fig. 3. The success probability (Ptotal) of the two ECPs as a function of the initial entanglement coefficient α, after they have been operated for k times. For numerical simulation, we choose k = 1, 3, 5, respectively.
4. Discussion

In the paper, we presented two efficient ECPs for distilling the maximally entangled N-photon NOON state from an arbitrary less-entangled NOON state. It is interesting to compare these two ECPs with our previous ECP for the N-photon NOON state.[44] In the ECP of Ref. [44], the parties need to consume two pairs of less-entangled NOON states to distill one pair of maximally entangled NOON state, while the current two ECPs only require one pair of less-entangled NOON state and an auxiliary single photon, which can reach the same high success probability as that in Ref. [44]. zhouqip1. As the NOON state is quite precious, the current two ECPs are more economical. On the other hand, the previous ECP in Ref. [44] zhouqip1 require the two parties to take the coincidence measurement for a pair of NOON state, which will increase the operation difficulty, especially when the photon number N is large. In the current two ECPs, we only need to measure the auxiliary single photon, which can simplify the operation largely. Therefore, the two current ECPs are more advantageous than the previous one.

Comparing the two current ECPs, it looks that if we change the spatial modes c1 and c2 to b1 and b2, and make the transmittance of the VBS meet t = 0.5, the second ECP can be transformed to the first ECP. However, it is noteworthy that the second ECP is more optimal than the first one. In the first ECP, the auxiliary photon should be shared by Alice and Bob in two distant locations. It requires the entangled photon source, which is precious under current experimental condition. Moreover, after passing through the QND gate, the two parties need to make the coincidence measurement of the auxiliary single-photon entangled state, which is difficult in practical experiment. Moreover, in the first ECP, the auxiliary photon in Alice’s hand should be sent back and will be transmitted for a second time. As pointed out by Ref. [94], the decoherence and photon loss are unavoidable during the transmission process due to the environmental noise. It will limit the application of the first ECP in the practical applications. Fortunately, in the second ECP, the auxiliary photon entanglement can be created locally with the help of the VBS and only possessed by Bob. Only Bob needs to operate this concentration process, which makes this ECP more advantageous in practical applications.

In the second ECP, the VBS is the key element for creating the local single-photon entanglement. According to the initial coefficients of the less-entangled NOON state, the parties should provide the VBSs with the transmittance of

in the k-th concentration round. Certainly, in the first ECP, the single-photon entanglement created by S2 can also be reviewed as the single-photon source plus the VBS. The VBS is a common optical element in current technology. In 2012, Osorio et al. reported their experimental results about the heralded photon amplification for quantum communication with the help of the VBS.[95] amplification They adjusted the transmittance of VBS to increase the probability of the single photon |1〉 from a mixed state ηt|1〉〈1| + (1−ηt)|0 〉〈0|. In their protocol, they adjust the splitting ratio of VBS from 50:50 to 90:10 to increase the visibility from (46.7 ± 3.1%) to (96.3 ± 3.8%). Based on their results, it is believed that our requirement for VBS can be realized under current experimental condition.

Finally, we will discuss another key element of both ECPs, that is, the cross-Kerr nonlinearity. Although the cross-Kerr nonlinearity has been widely discussed in quantum information processing,[80,81,83–85,96] it has been regarded as a controversial topic in practical experiment for a long time.[97–99] First, the qubit states may degrade to the mixed states in the homodyne detection process.[100,101] Second, the natural cross-Kerr nonlinearity is extremely weak, so that it is difficult to discriminate two overlapping coherent states in homodyne detection. Fortunately, the decoherence can be extremely weak simply by an arbitrary strong coherent state associated with a displacement D (−α) performed on the coherent state.[100] On the other hand, it is possible to obtain an observable cross-Kerr phase shift with the help of the weak measurement.[102] As early as 2003, Hofmann showed that with the help of a single two-level atom trapped in a one-sided cavity, we can obtain a phase shift as large as π.[103] Meanwhile, as shown in Ref. [104], large cross-Kerr nonlinearities were also obtained in a double-quantum-well structure with a four-level, double-type configuration. The “giant” cross-Kerr effect with phase shift of 20° per photon has been observed in the current experiment.[105] Recent work of the Xiao group also showed that the Rydberg atom system can generate large cross phase between photons.[106] According to the recent theoretical and experimental works based on cross-Kerr nonlinearity, the cross-Kerr nonlinearity may provide its practical application in the future quantum information processing.

5. Summary

In summary, we put forward two efficient ECPs for distilling the maximally entangled N-photon NOON state from arbitrary less-entangled NOON state. In both ECPs, we only require one pair of less-entangled NOON state and an auxiliary single photon to complete the task. Moreover, with the help of the cross-Kerr nonlinearity, both ECPs can be used repeatedly. In this way, they can both obtain high success probability. Comparing with our previous ECP of the NOON state, the two current ECPs are more economical and easy to operate. In the first ECP, the auxiliary single photon should be shared by the two parties, and the two parties need to take the coincidence measurement for the auxiliary photon. The second ECP is more optimal than the first one. In the second ECP, the auxiliary single photon is only possessed by Bob benefitting from the VBS, which can reduce the requirement for the single-photon source. Meanwhile, as all the operations are local, the second ECP is easier to operate than the first one. In particular, in the second ECP, as the auxiliary single photon does not need to transmit in a long-distance channel, the second ECP can effectively reduce the docoherence and photon loss in the transmission process. In this way, the second ECP is more advantageous in practical applications. Based on the features described above, our two ECPs, especially the second ECP may be useful and convenient in quantum information processing.

Reference
1Bennett C HBrassard GCrepeau CJozsa RPeres AWootters W K 1993 Phys. Rev. Lett. 70 1895
2Karlsson ABourennane M 1998 Phys. Rev. A 58 4394
3Bennett C HWiesner S J 1992 Phys. Rev. Lett. 69 2881
4Hillery MBuzek VBerthiaume A 1999 Phys. Rev. A 59 1829
5Wei H RDeng F G 2013 Phys. Rev. A 87 022305
6Feng G RXu G FLong G L 2013 Phys. Rev. Lett. 110 190501
7Wei H RDeng F G 2013 Opt. Express 21 17671
8Long G LLiu X S 2002 Phys. Rev. A 65 032302
9Deng F GLong G LLiu X S 2003 Phys. Rev. A 68 042317
10Wang CDeng F GLi Y SLiu X SLong G L 2005 Phys. Rev. A 71 044305
11Chang YXu C XZhang S BYan L 2014 Chin. Sci. Bull. 59 2541
12Liu Y 2013 Chin. Sci. Bull. 58 2927
13Liu YOu-Yang X P 2013 Chin. Sci. Bull. 58 2329
14Su X LJia X JXie C DPeng K C 2014 Sci. Chin.-Phys. Mech. Astron. 57 1210
15Zou X FQiu D W 2014 Sci. Chin.-Phys. Mech. Astron. 57 1696
16Chang YZhang S BYan L LHan G H 2015 Chin. Phys. B 24 080306
17Chang H HJino HJong I LHyung J Y 2014 Chin. Phys. B 23 090309
18Ji Y QJin ZZhu A DWang H FZhang S 2014 Chin. Phys. B 23 050306
19Zhao J JGuo X MWang X Y 2013 Chin. Phys. Lett. 30 060302
20Wu H ZYang Z B 2014 Chin. Phys. Lett. 31 024206
21Tang S QYuan J BWang X WKuang L M 2015 Chin. Phys. Lett. 32 040303
22Gu BHuang Y GFang XChen Y L 2013 Int. J. Theor. Phys. 52 4461
23Huelga S FMacchiavello CPellizzari TEkert A K 1997 Phys. Rev. Lett. 79 3865
24Resch K JPregnell K LPrevedel RGilchrist APryde G JÓBrien J LWhite A G 2007 Phys. Rev. Lett. 98 223601
25Mitchell M WLundeen J SSteinberg A M 2004 Nature 429 161
26Walther PPan J WAspelmeyer MUrsin RGasparoni SZeilinger A 2004 Nature 429 158
27Nagata TOkamoto RÓBrien J LSasaki KTakeuchi S 2007 Science 316 726
28Hua MTao M JDeng F G 2014 Chin. Sci. Bull. 59 2829
29Bohmann MSperling JVogel W 2015 Phys. Rev. A 91 042332
30Boto A NKok PAbrams D SBraunstein S LWilliams C PDowling J P 2000 Phys. Rev. Lett. 85 2733
31Bollinger J JItano W MWineland D JHeinzen D J 1996 Phys. Rev. A 54 R4649
32Eckert KHyllus PBruss D 2006 Phys. Rev. A 73 013814
33D’ngelo MChekhova M VShih Y 2001 Phys. Rev. Lett. 87 013602
34Sun F WOu Z YGuo G C 2006 Phys. Rev. A 73 032308
35Liu BOu Z Y 2010 Phys. Rev. A 81 033823
36Bennett C HBernstein H JPopescu SSchumacher B 1996 Phys. Rev. A 53 2046
37Bose SVedral VKnight P L 1999 Phys. Rev. A 60 194
38Shi B SJiang Y KGuo G C 2000 Phys. Rev. A 62 054301
39Zhao ZPan J WZhan M S 2001 Phys. Rev. A 64 014301
40Yamamoto TKoashi MImoto N 2001 Phys. Rev. A 64 012304
41Sheng Y BDeng F GZhou H Y 2008 Phys. Rev. A 77 062325
42Sheng Y BZhou LZhao S MZheng B Y 2012 Phys. Rev. A 85 012307
43Sheng Y BZhou LZhao S M 2012 Phys. Rev. A 85 042302
44Zhou LSheng Y BCheng W WGong L YZhao S M 2013 Quantum. Inform. Process. 12 1307
45Deng F G 2012 Phys. Rev. A 85 022311
46Wang C 2012 Phys. Rev. A 86 012323
47Sheng Y BZhou LWang LZhao S M 2013 Quantum. Inform. Process. 12 1885
48Zhou LSheng Y BCheng W WGong L YZhao S M 2013 J. Opt. Soc. Am. B 30 71
49Zhou L 2013 Quantum Inf. Process. 12 2087
50Zhou LSheng Y B 2014 Opt. Commun. 313 217
51Zhou LSheng Y BZhao S M 2013 Chin. Phys. B 22 020307
52Ren B CDu F FDeng F G 2013 Phys. Rev. A 88 012302
53Ren B CDeng F G 2013 Laser Phys. Lett. 10 115201
54Sheng Y BZhou L 2013 Entropy 15 1776
55Du F FDeng F G 2015 Sci. China-Phys. Mech. Astron. 58 040303
56Zhao JZheng C HShi PRen C NGu Y J2014Opt. Commun.232
57Gu BHuang Y GFang XWang H B 2014 Int. J. Theor. Phys. 53 1337
58Sheng Y BFeng Z FOu-Yang YQu C CZhou L 2014 Chin. Phys. Lett. 31 050303
59Wang G YLi TDeng F G 2015 Quantum Inform. Process. 14 1305
60Sheng Y BZhou LCheng W WGong L YZhao S MZheng B Y 2012 Chin. Phys. B 21 030307
61Feng Z FOu-Yang YZhou LSheng Y B 2015 Opt. Commun. 340 80
62Cao CDing HLi YWang T JMi S CZhang RWang C 2015 Quantum Inform. Process. 14 1265
63Cao CWang T JZhang RWang C 2015 Laser Phys. Lett. 12 036001
64Wang CCao CHe L YZhang C L 2014 Quantum Inform. Process. 13 1025
65Li X HGhose S 2015 Phys. Rev. A 91 062302
66Zhou L 2014 Chin. Phys. B 23 050308
67Sheng Y BOu-Yang YZhou LWang L 2014 Quantum Inform. Process. 13 1595
68Sheng Y BPan JGuo RZhou LWang L 2015 Sci. China-Phys. Mech. Astron. 58 060301
69Li TDeng F G 2014 Int. J. Theor. Phys. 53 3026
70Shukla CBanerjee APathak A 2015 Quantum Inform. Process. 14 2077
71Choudhury BDhara A 2013 Quantum Inform. Process. 12 2577
72Si BWen J JCheng L YWang H FZhang SYeon K H 2014 Int. J. Theor. Phys. 53 80
73Choudhury B SDhara A. 2013 Int. J. Theor. Phys. 52 3965
74Fan L LXia YSong J 2014 Quantum Inform. Process. 13 1967
75Liu JZhao S YZhou LSheng Y B 2014 Chin. Phys. B 23 020313
76Sheng Y BZhou L 2013 Chin. Phys. B 22 110303
77Li X HGhose S 2014 Laser Phys. Lett. 11 125201
78Gu B 2012 J. Opt. Soc. Am. B 29 1685
79Nemoto KMunro W J 2004 Phys. Rev. Lett. 93 250502
80Lin QLi J 2009 Phys. Rev. A 79 022301
81Barrett S DKok PNemoto KBeausoleil R GMunro W JSpiller T P 2005 Phys. Rev. A 71 060302
82Xia YChen Q QSong JSong H S 2012 J. Opt. Soc. Am. B 29 1029
83He BRen YBergou J A 2009 Phys. Rev. A 79 052323
84He BScherer A 2012 Phys. Rev. A 85 033814
85He BLin QSimon C 2011 Phys. Rev. A 83 053826
86Xiu X MDong LShen H ZGao Y JYi X X2014Quantum Inform. Process.14236
87Dong LXiu X MShen H ZGao Y JYi X X 2013 Opt. Commun. 308 304
88Heo JHong C HLim J IYang H J 2015 Chin. Phys. B 24 050304
89Jeong H 2005 Phys. Rev. A 72 034305
90Lin QHe B 2015 Sci. Rep. 5 12792
91Yan XYu Y FZhang Z M 2014 Chin. Phys. B 23 060306
92Wang Z HZhu LSu S LGuo QCheng L YZhu A DZhang S 2013 Chin. Phys. B 22 090309
93Munro W JNemoto KBeausoleil R GSpiller T P 2005 Phys. Rev. A 71 033819
94Duan L MLukin M DCirac J IZoller P 2001 Nature 414 413
95Osorio C IBruno NSangouard NZbinden HGisin NThew R T 2012 Phys. Rev. A 86 023815
96Lin QHe B 2009 Phys. Rev. A 80 042310
97Gea-Banacloche J 2010 Phys. Rev. A 81 043823
98Shapiro J H 2006 Phys. Rev. A 73 062305
99Shapiro J HRazavi M 2007 New J. Phys. 9 16
100Jeong H 2006 Phys. Rev. A 73 052320
101Barrett S DMilburn G J 2006 Phys. Rev. A 74 060302
102Feizpour AXing XSteinberg A M 2011 Phys. Rev. Lett. 107 133603
103Hofmann H FKojima KTakeuchi SSasaki K 2003 J. Opt. B: Quantum Semiclass. Opt. 5 218
104Zhu CHuang G 2011 Opt. Express 19 23364
105Hoi I CKockum A FPalomaki TStace T MFan BTornberg LSathyamoorthy S RJohansson GDelsing PWilson C M 2013 Phys. Rev. Lett. 111 053601
106He BSharypov A VSheng JSimon CXiao M 2014 Phys. Rev. Lett. 112 133606