Quantum frequency conversion (QFC) has been proposed to connect telecommunication wavelength light (carrier) with atomic transitions (quantum memories)^[1,2] and improvement of optical detection,^[3] by using the nonlinear effect in nonlinear media χ⁽²⁾ and χ⁽³⁾. It can be used to change the frequency of a quantum state to a desired one.^[4,5] It is proved that the properties of quantum states of light can be maintained during QFC, including non-classical correlation,^[6] entanglement,^[7] non-classical photon statistics,^[8–11] photon coherence,^[12,13] and orbital angular momentum.^[14] Recently, the successful experiments of spectral compression of single photons,^[15] infrared or mid-infrared up-conversion imaging,^[16,17] and quantum up-conversion of squeezed states^[18,19] has aroused interest in exploring more applications of QFC. A direct quantum interface between photonic qubits of widely different wavelengths was demonstrated in Ref. [7]. In their work, the energy–time entanglement of a photon at 1310 nm with a photon at 1550 nm was transferred to that of another photon at a wavelength of 710 nm via sum-frequency generation (SFG). It is verified that the entanglement is unaffected, though one of the two entangled photons is transferred by an up-conversion process. As 710-nm wavelength is close to alkaline atomic transition and the transmission wavelengths for photons in optical fibers are 1310 nm and 1550 nm,^[20,21] the converted entanglement can be used for quantum networks based on atoms and photons.^[22]

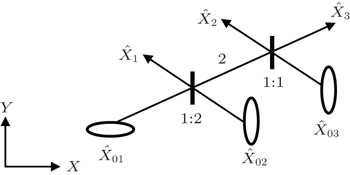
On the other hand, it is known that when three continuous variable (CV) single-mode squeezed states input on two beam splitters, a tripartite CV entangled state is yielded. In Ref. [23], the squeezing direction of mode 1 is Y, the other modes are squeezed in X as shown in Fig. 1, and the three output modes are all genuinely tripartite entangled states. In this paper, we analyze an intracavity scheme with frequency doubling of the tripartite entangled states. The tripartite entangled fields at 1560 nm are transferred to the three-mode entanglement at 780 nm, by the process of second harmonic generation, which is a special process of up-conversion. As 780 nm is the absorption line of Rb atom, the produced entanglement can be used in an atom system.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Scheme for producing the tripartite entangled state of modes 1, 2, and 3 with three single squeezed states (one state is squeezed in Y direction, the other two are squeezed in X direction) and two beam splitters (one is 1:2 BS and the other is 1:1).

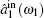
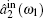
The scheme of frequency doubling process is depicted in Fig. 2. The tripartite entangled beams from a three-port device called a tritter^[24] (Fig. 1), , , and , are frequency-degenerated and injected into three one-sided cavities. Each cavity consists of a second-order nonlinear crystal, which provides the interaction of type-I second harmonic generation (SHG). The output fields , , and are all of frequency ω₂ = 2ω₁.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Scheme of physical system for frequency doubling using cavity. 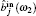are the incoming tripartite entangled fields and are the three outgoing fields. Type-I SHG takes place in each cavity.

The input–output relations of the amplitude quadrature components and phase quadrature components on the field modes from the tritter are given in Ref. [23]:

It is found that it is easy for the variances to be below the shot noise limit (SNL) and the perfect entanglement can be obtained with infinite squeezing (r₁ = r₂ → ∞) in single-mode squeezed states.

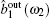
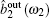
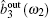
We will discuss the process of SHG and analyze the preserved tripartite entanglement among the output fields , , in the next section.

Under the assumption of perfect phase matching and zero detuning, the Hamiltonian describing the interaction in the cavity can be written as

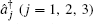
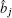
Assuming that nonlinear coefficient κ and loss coefficient γ are the same for all cavities, the quantum Langevin equations of motion for the cavity modes can be expressed as

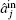
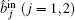
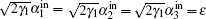
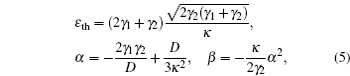
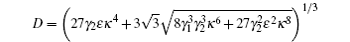
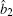
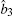
In the symmetric case, we set the steady-state amplitudes of the fundamental modes α₁ = α₂ = α₃ = α and . Following the semiclassical method, the threshold to the beginning of the self-pulsing is given by ɛ_th and the steady-state solutions below the threshold are found to be

The linearized equations of motion for quadrature-phase amplitude may be written in a matrix form by setting the following relations â_j = α_j + δ â_j, 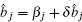, and X̂ = δ â + δ â^†, Ŷ = (δ â − δ â^†)/i,

According to the boundary condition of the coupling mirrors 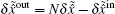, , we can obtain the fluctuation of output fields at the analysis frequency ω^[25]

According to Eq. (1), the input fluctuation of â₁, â₂, and â₃ can be expressed as:

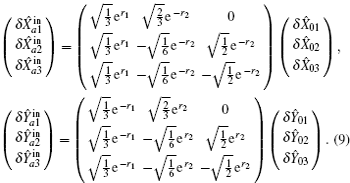
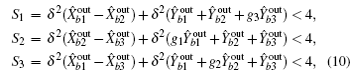
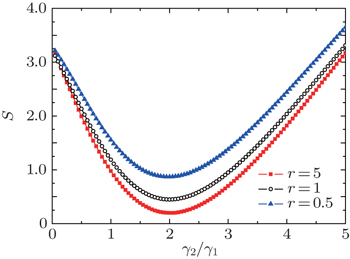
Because the variances of the relative amplitude quadratures and total phase quadratures of the input tripartite entanglement are identical and we have assumed the parameters of the three cavities to be the same, the correlation spectra S₁ = S₂ = S₃ = S. The dependences of S on the normalized analysis frequency Ω = ω τ/γ₁ under different squeezed factor are shown in Fig. 3. Obviously, the maximum correlation (S is minimum) is obtained at low frequency. For the low frequency, if the initial squeezing factor r₂ = r₁ = r becomes larger, the preserved correlation among b₁, b₂, and b₃ is better. But for the high frequency, the smaller the squeezing factor, the better the preserved correlation is, and we have a wider frequency range to measure the entanglement corresponding to smaller r. Figure 4 shows the correlation fluctuation spectra S versus pump parameter σ = ɛ/ɛ_th for different values of squeezing factor r. The tripartite entanglement is retained at low pump power. It is obvious that the better correlation is obtained with larger r. But for a given r, we have an optimal pump parameter (σ around 0.12) where S reaches a minimum. In addition, the optimal cavity parameters should be chosen to meet the smallest S for preserving the quantum correlation as shown in Fig. 5. If the amplitude transmission coefficient of harmonic mode is twice that of fundamental mode, the maximum entanglement is maintained.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Correlation fluctuation spectra S versus the normalized analysis frequency Ω, pump parameter σ = 0.1, transmission of the output coupler mirror γ2/γ1 = 2. The squares, circles, and triangles are for squeezing factor r = 5, 1, 0.5 respectively.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Correlation fluctuation spectra S at Ω = 0 versus pump parameter σ for different values of squeezing factor r, the transmission of the output coupler mirror γ2/γ1 = 2. The squares, circles, and triangles are for squeezing factor r = 5, 1, 0.5 respectively.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Correlation fluctuation spectra S at Ω = 0 versus transmission of the output coupler mirror γ2/γ1 for different values of squeezing factor (r = 5, 1, 0.5), the pump parameter σ = 0.12. The squares, circles, and triangles are for squeezing factor r = 5, 1, 0.5 respectively.

We propose a scheme to preserve the tripartite entanglement based on the process of SHG in three cavities, and it can be realized when the cavity operates far below the threshold. The dependences of the correlation spectrum on the parameters of cavity, the analysis frequency, and the initial squeezing are discussed. The entangled state conversion between different frequencies can be used to connect the atom with light in a quantum communication network, and the experimental scheme can be realized with the matured entanglement technology.