† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11171208), the Natural Science Foundation of Zhejiang Province, China (Grant No. LY15A020007), the Natural Science Foundation of Ningbo City (Grant No. 2014A610028), and the K. C. Wong Magna Fund in Ningbo University, China.
By employing the improved moving least-square (IMLS) approximation, the improved element-free Galerkin (IEFG) method is presented for the unsteady Schrödinger equation. In the IEFG method, the two-dimensional (2D) trial function is approximated by the IMLS approximation, the variation method is used to obtain the discrete equations, and the essential boundary conditions are imposed by the penalty method. Because the number of coefficients in the IMLS approximation is less than in the moving least-square (MLS) approximation, fewer nodes are needed in the entire domain when the IMLS approximation is used than when the MLS approximation is adopted. Then the IEFG method has high computational efficiency and accuracy. Several numerical examples are given to verify the accuracy and efficiency of the IEFG method in this paper.
As a fundamental model to describe the nonlinear phenomenon of nature, the nonlinear Schrödinger (NLS) equation is widely used in kinds of fields, such as nonlinear optical medium,[1–3] photonics,[4] plasmas,[5] Bose–Einstein condensates,[6,7] quantum mechanics,[8] electro-magnetic wave propagation,[9] underwater acoustics,[10–12] etc.
The Schrödinger equation has been widely explored and investigated in the last few years. The methods of numerical modeling for Schrödinger equation have been put forward by finite difference schemes,[13] a Crank–Nicolson implicit scheme,[14] higher-order compact scheme,[15] radial basis functions,[16] a fully implicit formula,[17] meshless local Petrov–Galerkin (MLPG) method,[18] and the dual reciprocity boundary element method (DRBEM),[19] and so on.
As important numerical methods, meshless methods[20,21] have been used for solving many complicated problems in science and engineering. It is important to develop various meshless methods of solving linear and nonlinear problems accurately and efficiently.[22–24] The moving least-square (MLS) approximation was first used for data fitting.[25] The MLS technique has been applied to the analysis of solid mechanics and often used to construct shape function in the element-free Galerkin (EFG) method.[20] The EFG method is one of the most important meshless methods that have attracted much attention of researchers.[20] This method does not require any element connectivity data, and does not suffer much degradation in accuracy when nodal arrangements are very irregular. The method has been successfully applied to a lot of science and engineering problems, such as elasticity, heat conduction, and crack growth. The MLS technique is derived from the traditional least squares method, which means that the least squares method is used at each computing point in the actual process of calculation procedure. Unfortunately, the algebraic equation system in the MLS method is sometimes ill-conditioned. In order to solve this problem, Cheng and Chen presented the improved moving least-square (IMLS) approximation.[26] In the IMLS approximation, the basis function is chosen as an orthogonal function system, and the resulting final algebraic equation system is not ill-conditioned. Based on the IMLS approximation, the boundary element-free method is used for studying the elasticity, fracture, elastodynamics and potential problems.[27–30] The improved element-free Galerkin (IEFG) method is a combination of IMLS approximation and EFG method. In the IEFG method,[31–34] fewer nodes are selected in the entire domain than in the conventional EFG method. Hence, the IEFG method will definitely increase the computational efficiency. Furthermore, the IEFG method has greater computational accuracy with the same nodes than the EFG method. None of the shape functions of the MLS approximation and the IMLS approximation satisfies the property of Kronecker δ function. In order to overcome the disadvantage, Ren et al. presented Lancaster’s improved IMLS method.[35] Based on the new shape function of IMLS method, Ren and Cheng presented interpolating element-free Galerkin (IEFG) method and interpolating boundary element-free method for potential and elasticity problems,[35–38] and the corresponding mathematical theory was discussed.[39] Cheng and Liew presented the IMLS Ritz and Kp Ritz method to solve heat conduction problem, wave problem and Sine-Gordon equation.[40–43] Wang et al. put forward the interpolating element-free method and the interpolating boundary element-free method with nonsingular weight function.[44–46] Based on the complex variable moving least-square (CVMLS) approximation and the complex variable reproducing kernel particle method (CVRKPM), the meshless method with complex variable has been presented. Chen et al. presented the complex variable reproducing kernel particle method (CVRKPM) for two-dimensional (2D) elastoplasticity, elastodynamics problems and the analysis of Kirchhoff plates.[47–49] Cheng et al. presented the complex variable element-free Galerkin (CVEFG) method of investigating the elasticity, elastoplasticity, viscoelasticity and large deformation problems.[50–53] Based on an improved CVMLS approximation, an improved complex variable element-free Galerkin method has been developed to solve the 2D elasticity problems and elastoplasticity.[54,55] Deng et al. presented an interpolating complex variable element-free Galerkin method of solving the temperature field problems.[56]
The improved element-free Galerkin (IEFG) method for the 2D unsteady Schrödinger equation is developed in this paper. In the IEFG method, the trial functions are approximated by the IMLS technique, the energy functional and the final algebraic equation system that is gained via the Galerkin method, the boundary conditions are imposed by penalty function. Numerical examples show that the present technique leads to good accuracy and efficiency.
Consider the following 2D unsteady Schrödinger equation:





By taking variation and the subsection integration of Eq. (

In the IMLS approximation, we define the following local approximation:

Define a functional as





By solving the extremum of J, we can find the coefficients


If p1 (






From Eq. (


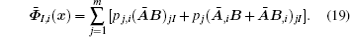
The cubic spline weight function is chosen as






From Eq. (






Substituting Eqs. (






Since


Substituting Eqs. (

Separate the real part from the imaginary part of Eq. (

By using the center difference method, we make the discretization of Eq. (

Equation (

The numerical results of 2D Schrödinger equation by the IEFG method can be obtained through solving Eq. (
In this section, three numerical examples are demonstrated to verify the efficiency and accuracy of the IEFG method. The implementation of the IEFG method is also presented. In all numerical examples, cubic spline function is chosen as a weight function, and the linear basis function is used.
Consider Eq. (






The analytical solution is

The IEFG method is used to solve the above equation with penalty factor α = 105 and dmax = 2.3 in time steps of Δt = 0.01. Figure
| Table 1. Relative errors and CPU times for the IEFG method at the time t = 2. . |
| Table 2. Dependences of relative error on node number for the IEFG method at t = 1. . |
Consider the case f(x,y) = 0 in Eq. (


The IEFG method is used with penalty factor α = 105 and dmax = 2.3 in time steps of Δt = 0.01.
Figure
Consider Eq. (


The initial and boundary conditions are easily derived from Eq. (




The IEFG method is used with penalty factor α = 105 and dmax = 2.3 in time steps of Δt = 0.01. Figure
From these figures, it is evident that the present numerical results obtained by the IEFG method are in excellent agreement with the analytical solutions.
The IEFG approach to solving 2D Schrödinger equation is developed and numerically implemented in the present work. The IMLS approximation is used to approximate the 2D trial function. By using the variation method, the final algebraic equation system is obtained due to energy functional. In the IMLS approximation, the basis function is chosen as an orthogonal function system, and the resulting final equation system is no more ill-conditioned due to involving no inverse matrix. It is demonstrated that the IMLS technique has a higher efficiency and precision than the traditional MLS approximation. Owing to its simple implementation, the IEFG method has the potential to replace the difference method and the finite element method for solving 2D Schrödinger equation and any other nonlinear partial differential equation.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 |

















