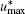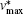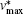Cite this Article
Lei Juan-Mian, Peng Xue-Ying. Improved kernel gradient free-smoothed particle hydrodynamics and its applications to heat transfer problems. Chinese Physics B, 2016, 25(2): 020202  
Permissions
Improved kernel gradient free-smoothed particle hydrodynamics and its applications to heat transfer problems
Lei Juan-Mian†, , Peng Xue-Ying
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China

 

† Corresponding author. E-mail: leijm@bit.edu.cn

Abstract
Abstract

Kernel gradient free-smoothed particle hydrodynamics (KGF-SPH) is a modified smoothed particle hydrodynamics (SPH) method which has higher precision than the conventional SPH. However, the Laplacian in KGF-SPH is approximated by the two-pass model which increases computational cost. A new kind of discretization scheme for the Laplacian is proposed in this paper, then a method with higher precision and better stability, called Improved KGF-SPH, is developed by modifying KGF-SPH with this new Laplacian model. One-dimensional (1D) and two-dimensional (2D) heat conduction problems are used to test the precision and stability of the Improved KGF-SPH. The numerical results demonstrate that the Improved KGF-SPH is more accurate than SPH, and stabler than KGF-SPH. Natural convection in a closed square cavity at different Rayleigh numbers are modeled by the Improved KGF-SPH with shifting particle position, and the Improved KGF-SPH results are presented in comparison with those of SPH and finite volume method (FVM). The numerical results demonstrate that the Improved KGF-SPH is a more accurate method to study and model the heat transfer problems.

PACS: 02.60.Cb;02.60.Lj;44.10.+i;44.25.+f;
Keyword:kernel gradient free-smoothed particle hydrodynamics;heat conduction;natural convection;accuracy and stability;
1. Introduction

Grid-based numerical methods such as the finite element method (FEM) and finite difference method (FDM) have been widely applied to various fields of computational fluid dynamics (CFD) and computational solid dynamics (CSD). However, conventional grid-based methods suffer some inherent difficulties in many aspects, such as mesh generation for irregular or complex geometry and cases with heavily distorted mesh. So many meshless methods have been developed over the past twenty years, such as element-free Galerkin method,[1–3] complex variable meshless method,[4,5] finite point method,[6] reproducing kernel particle method,[7–9] smoothed particle hydrodynamics,[10,11] moving particle semi-implicit method,[12] and corrective smoothed particle method.[13]

Smoothed particle hydrodynamics (SPH)[14] is a transient, Lagrangian method, proposed by Lucy,[15] Gingold and Monaghan[16] in 1977. The SPH was originally invented for modeling the astrophysical phenomena in three-dimensional (3D) open space, and now has been widely applied to fluid dynamics such as numerical simulation of quasi-incompressible flows,[17] multi-phase flows[18] and heat conduction.[19] In the SPH, a set of particles associated with physical properties are used to represent the state of the system. Since these particles can move within the computational domain in the Lagrangian frame, SPH is an attractive tool to model complex flows with free surfaces, moving interfaces and large deformations which are difficult for grid-based methods. Though the SPH has a very wide range of applications in incompressible flows,[20–22] applications in heat transfer problems are still not mature enough.

Natural convection in a closed square cavity is a classic convection heat transfer problem, which is important not only for understanding heat transfer phenomena but also for studying problems such as cooling of electrical equipment, nuclear reactor systems and crystal growth in liquids.[23] Hence, studies of heat transfer problems and obtaining their accurate solutions are still significant. In 1998, by using the SPH, Cleary[24] modeled natural convective flows in a differentially heated square cavity for low and moderate Rayleigh numbers (102, 104, 105). The results showed that the SPH is sufficient to give excellent isotherms for low Ra, but when Ra = 105, obvious deviations appear between SPH results and FEM results. Chaniotis et al.[25] used the remeshed SPH to simulate natural convection in a differentially heated cavity, displayed the contours of temperature and vorticity for Ra = 103 and 104, and the relative error between the remeshed SPH solution and the benchmark solution of de Vahl Davis is less than 8%. Szewc et al.[26] modeled natural convection with SPH based on non-Boussinesq formulation, the local Nusselt number distributions look very realistic, but contours for temperature and velocity are not smooth. Though it has been widely used in the field of solid mechanics and fluid mechanics, the conventional SPH is still poor in stability and accuracy.

One of the factors causing SPH instability is the non-uniform particle distribution.[27] In the Lagrangian numerical simulation, particles move along the streamlines, which will cluster or scatter under certain conditions, such as natural convection. What is more, the non-physical behavior of the kernel function will weaken the interaction between particles when particle distances are within a close range. Then particles will continue to cluster, which will reduce the precision or interrupt the numerical simulation, so it is necessary to correct the particle position. In 2008, Nester et al.[28] proposed a particle velocity correction, and applied this method to the finite volume particle method (FVPM) to maintain the uniformity of the moving particle cloud. In 2009, particle velocity correction was improved by Xu et al.,[29] and the new approach called shifting particle position maintains accuracy and stability when simulating Taylor–Green vortices and vortex spin-down problems. In 2012, Hashemi et al.[30] applied shifting particle position to SPH, the numerical results demonstrate that shifting particle position can alleviate defects produced by non-uniform distribution of particles and improve the stability of the numerical method. Shifting particle position not only needs less computational time but also effectively maintains the uniformity of particle distribution. Hence, this paper uses shifting particle position to weaken the non-uniform particle distribution effects on numerical simulation.

At present, in order to overcome the low accuracy of the conventional SPH, a large number of methods have been proposed. Finite particle method (FPM)[31] is an enhanced version of SPH, in which the function and its first derivatives are calculated simultaneously to restore the particle consistency and improve the approximation accuracy. Zhang and Batra[32] used numerical tests to show the FPM superiority over the CSPM, and the simulation results of the 2D transient heat conduction problems demonstrate that FPM is more accurate than CSPM. Liu et al.[31] modeled the classic Poiseuille flow, Couette flow, shear driven cavity and a dam collapsing problem by FPM, and the numerical examples showed that the FPM is a very attractive alternative for simulating incompressible flows. On the basis of FPM, Huang et al.[33] substituted the product of particle distance and kernel function for kernel gradient in FPM since the kernel gradient is not necessary in the whole computation, and this new approach is referred to as a kernel gradient free-SPH (KGF-SPH). KGF-SPH widens the selection of the kernel function, improves the simulation precision and simplifies the solving process because of the symmetric property of the corrective matrix. However, the conventional FPM and KGF-SPH differentiate the first derivatives to obtain the second derivatives, and the errors of the first derivatives will be brought into the second derivatives, which will reduce the accuracy of the simulation results.

In the present paper, the Improved KGF-SPH is proposed, which modifies the two-pass model in KGF-SPH with a new kind of discretization scheme for the Laplacian. Simple (1D and 2D heat conduction) and complex (natural convection in a closed square cavity) heat transfer problems are simulated by the Improved KGF-SPH. The rest of this paper is organized as follows. The conventional SPH, KGF-SPH, and Improved KGF-SPH are introduced in Section 2. In Section 3, the Improved KGF-SPH formulations for the governing equations and the state equation are briefly depicted. In Section 4, the particle shifting position is presented in detail. In Section 5, the 1D and 2D heat conduction problems are adopted to test the precision and stability of the Improved KGF-SPH. In Section 6, natural convection in a closed square cavity is modeled by the Improved KGF-SPH with shifting particle position. In Section 7, some conclusions are drawn from the present research results.

2. Numerical methods
2.1. SPH

The concept behind SPH is based on an interpolation scheme, and in SPH, any function or physical property can be approximated by its value at a set of disordered points. The formulations of SPH are often divided into two key steps: the first step is the integral representation or the so-called kernel approximation of physical properties, the second one is the particle approximation of physical properties. In the first key step, for an arbitrary function f, the kernel approximation of the function value f (ri) and its first derivatives ∇ f (ri) at r = ri are respectively[14]

where f (rj) is the function value at r = rj, W(ri − rj, h) is the kernel function, h is the smoothing length, ∇iW(ri − rj, h) is the kernel gradients, and dV is the volume element.

In the particle approximation, the computational domain is discretized by a series of particles with some attributes such as mass, position, momentum and energy. Equations (1) and (2) can be written in the following form of discretized particle approximation:

where fi = f (ri), fj = f (rj), W = W(ri − rj, h), (∇ f)i = ∇ f (ri), and ∇iW = ∇iW(ri − rj, h). The subscript j represents the neighboring particle of particle i, mj and ρj represent mass and density of particle j respectively.

In 2D case, the most widely used SPH discretization scheme for the Laplacian is[34]

where α and β are the dimension indices repeated from x to y, rα and rβ represent the components of r in the α and β directions respectively,

and δαβ is the Dirac delta function: when α = β, δ = 1, when α ≠ β, δ = 0. According to Eq. (5), in 2D space, the discretization scheme for the Laplacian is

2.2. KGF-SPH

In 2015, based on FPM, Huang et al.[33] developed a kernel gradient free-SPH (KGF-SPH) which only involves kernel function itself in kernel and particle approximation. In the KGF-SPH, performing Taylor series expansion at a certain point r = ri and retaining the first order derivatives, an arbitrary function f (rj) can be expressed as follows:

where o(h2) is the remainder of the expansion. Multiplying both sides of Eq. (7) with W and (rj − ri)W respectively, ignoring the remainder of the expansion and integrating over the computational domain can yield the following equations:

Solving Eqs. (8) and (9) simultaneously, we have

The corresponding particle approximation of Eq. (10) can be expressed as

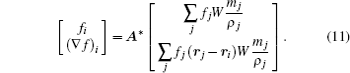
In 2D space, equation (11) can be rewritten as the following equation

The corrective matrix A* in Eq. (12) reads

where xji = xj − xi and yji = yj − yi.

It can be observed from Eq. (13) that the corrective matrix is symmetric, and the symmetry of the matrix can simplify the solving progress and save computational time. There is no kernel gradient in Eq. (12), so no matter whether the kernel function is differentiable, it can be applied in Eq. (12), thus KGF-SPH is a kernel gradient free meshless method.

The two-pass model, which obtains second derivatives by nesting two first derivative operations, is used to discretize the Laplacian in the conventional KGF-SPH. So in 2D space, the KGF-SPH discretization scheme for the Laplacian is

where

In the equations given above, fj,x and fj,y are the first derivatives of particle j in the x and y directions respectively. The subscript k represents the neighboring particle of particle j, xk j = xk − xj, yk j = yk − yj.

2.3. Improved KGF-SPH

In KGF-SPH, the Laplacian is calculated by using Eq. (14) based on the first derivatives. There are two disadvantages in doing so: (i) it increases computational cost because of the two-pass model needing two passes over all particles; (ii) it is difficult to implement the boundary conditions. When solving physical properties of fluid particles near the walls, the derivatives of virtual particles on the walls need to be solved first, so more virtual particles out of the walls are needed.

In order to overcome these two drawbacks, in this paper we propose a new discretization scheme to approximate the Laplacian, and apply it to the KGF-SPH. The following section provides the derivation process of the new Laplacian discretization scheme in detail.

In 2D space, performing Taylor series expansion at a nearby point (xi, yi) and retaining the second derivatives, a function f at point (xj, yj) can be expressed as follows:

where fi,xx and fi,yy are the second derivatives of particle i in the x and y directions respectively, fi,xy is the second order mixed partial derivative of particle i.

Multiplying both sides of Eq. (17) with kernel function W, and transposing can yield the following equation:

Integrating both sides of Eq. (18) over the computational domain, we obtain

The first and second terms on the right-hand side of Eq. (19) are both zero because of the symmetry of kernel function, so equation (19) can be simplified into

When particles are uniformly distributed in the computational domain, solving and in a polar coordinate, we have

Thus

Simplifying Eq. (20) by using Eq. (23) and transposing, the discretization scheme for the Laplacian can be written as

The corresponding particle approximation of Eq. (24) is

In order to alleviate defects produced by non-uniform distribution of particles, equation (25) is replaced with the following equation:

Equations (12) and (26) are the Improved KGF-SPH formulations in 2D space. The new discretization scheme for the Laplacian in Eq. (26) keeps the property of kernel gradient free, which is easy to deal with boundary conditions and has higher precision and better stability than the original KGF-SPH.

3. Basic equations
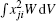
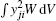
3.1. Governing equations

For natural convection in a closed square cavity, assuming the dynamic viscosity coefficient μ to be a constant, the governing equations in the Lagrangian frame are[14]

where t represents the time, ρ is the density, x and y are the spatial coordinates, u and v are the velocity components in the x and y directions respectively, p is the pressure, T represents the temperature, thermal diffusivity α = λ/(ρcp), λ being the thermal conductivity, and cp the specific heat capacity.

3.2. Improved KGF-SPH formulations

Using Eqs. (12), (13), and (26) to discretize Eqs. (27)–(30) can yield the Improved KGF-SPH formulations for natural convection in a closed square cavity as follows:

where uji = uj − ui, vji = vj − vi, and pji = pj − pi.

3.3. State equation

The above governing equation is not closed, so the state equation should be added. In this paper, the following weakly compressible state equation is used[17]

where ρ∞ is the reference density, c is the artificial sound speed, and its value is ten times as large as the maximum velocity.

4. Shifting particle position

In order to enhance numerical stability, shifting particle position can be used to maintain the uniformity of particles. Shifting particle position employed in this paper modifies the particle position, and the position shift δri reads

where C is a constant: the bigger the C value, the greater the effect of the method is, and C is set to be 0.5 in this paper; α is the shifting magnitude; Ri is the shifting vector of particle i; α and Ri are solved by the following equations:

where Umax is the maximum particle velocity, dt is the time step, Mi is the number of neighboring particles around particle i; ri j is the distance between particle i and particle j; nij is the unit distance vector between particle i and particle j; r̄i is the average particle spacing in the neighborhood of i, which reads

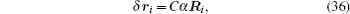
Since the particles are shifted, the physical properties carried by particles are also changed. The physical properties are corrected by the following equation:

where φ is a general variable representing any physical properties, i and i′ are the particle old position and its new position respectively. Shifting particle position can obtain an isotropic particle distribution, so it is used to improve numerical stability of natural convection in a closed square cavity.

5. Accuracy and stability test for the Improved KGF-SPH

In order to validate the Improved KGF-SPH, two simple conduction heat transfer problems are studied in this section. The Improved KGF-SPH results are compared with those from SPH, KGF-SPH, and analytical solutions to show the high accuracy and stability of the Improved KGF-SPH.

5.1. 1D heat conduction problem

The computational domain for 1D heat conduction in this paper is the line segment from 0 to 1, at t moment, the temperature T(x, t) is governed by the following heat conduction equation:

where T is the temperature, t is the time, and x is the particle position. The initial and boundary conditions are T(x, 0) = sinπx and T(0,t) = T(1,t) = 0, respectively. In this case, the analytical solution is given by

Figure 1 displays the particle distribution for 1D heat conduction. A total of 49 fluid particles are uniformly distributed in the computational domain with another 4 (2 on each side of the segment) virtual particles uniformly located on the boundaries. The particle spacing is Δ = L/50 = 0.02, the smoothing length is h = 1.3Δ. According to the CFL condition, the time step is set to be dt = 2 × 10−4 s.

Fig. 1. Particle distribution for 1D heat conduction.

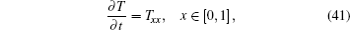
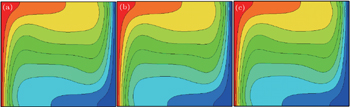
Figure 2 shows the comparison of the temperature profiles at t = 0.2 s for 1D heat conduction, computed by SPH, KGF-SPH, and Improved KGF-SPH with the analytical solution. It can be seen from Fig. 2 that the Improved KGF-SPH result accords very well with the analytical solution, the SPH result is smaller than the analytical solution, which indicates that SPH overestimates the heat transfer, while the KGF-SPH result oscillates violently near the analytical solution. Therefore, the Improved KGF-SPH gives better results than the other two methods, which has higher accuracy than SPH and better stability than KGF-SPH.

Fig. 2. Temperature profiles at t = 0.2 s for 1D heat conduction.
5.2. 2D heat conduction problem

In this section, the Improved KGF-SPH formulations are applied to the 2D heat conduction case with a simple square cavity geometry whose side length is L. At t moment, the temperature T(x,y,t) is governed by

with initial and boundary conditions being T(x,y,0) = 0, and T(0,y,t) = T(0.1,y,t) = T(x,0,t) = T(x,0.1,t) = 1, respectively.

Figure 3 is the schematic diagram and particle distribution for 2D heat conduction. The side length of the square cavity is L = 0.1 m, fluid particles are uniformly distributed in the computational domain, and virtual particles are distributed evenly on the boundary. The smoothing length is h = 1.3Δ, Δ is the particle spacing, and the time-step is dt = 10−6 s. As shown in Fig. 3, point A(0.005,0.01) is the monitor particle, so in this paper we will monitor the temperature history for point A.

Fig. 3. Schematic diagram and particle distribution for 2D heat conduction.

In order to verify our numerical method, the solution of the 2D heat conduction problem by the finite particle method (FVM) with 101×101 nodes is taken as a reference solution. For the SPH, KGF-SPH, and Improved KGF-SPH, 11×11 and 21×21 uniformly distributed particles are employed.

Figure 4 shows the comparison among the temperature distributions along the line x = 0.05 m at three times, i.e., t = 1.5 × 10−4, 3.0 × 10−4, and 4.5 × 10−4 s, computed with SPH, KGF-SPH, Improved KGF-SPH, and FVM. Because of the symmetry of the problem about the lines x = 0.05 m and y = 0.05 m, temperature distribution in the region y ∈ [0.05,0.1 m] is depicted. Figure 4(a) displays the results computed with 11×11 uniformly spaced particles. In Fig. 4(a), there are big errors between KGF-SPH results and FVM results. The SPH and Improved KGF-SPH results accord with the FVM results, but the Improved KGF-SPH results are much closer to those of FVM than the SPH results, particularly early on. Figure 4(b) shows results computed with 21×21 uniformly spaced particles, both the SPH and Improved KGF-SPH results in accordance with those obtained by FVM, while the KGF-SPH results deviate slightly from the FVM results. It can be seen from Fig. 4 that when employing more particles, the precision of KGF-SPH is significantly improved, but there are still deviations between the KGF-SPH results and FVM results, while the SPH and Improved KGF-SPH results accord well with the FVM results.

Fig. 4. Temperature distribution along the line x = 0.05 m for 2D heat conduction. (a) 11×11 particles, (b) 21×21 particles.

In order to show the Improved KGF-SPH superiority over SPH and KGF-SPH clearly, figure 5 presents the differences in temperature history for monitor particle A, obtained by SPH, KGF-SPH, and Improved KGF-SPH (based on 21×21 particles). Compared with the FVM results, the KGF-SPH results are poor, the SPH results are medium, and the Improved KGF-SPH results are good, so the accuracy of Improved KGF-SPH is higher than SPH and KGF-SPH. Since KGF-SPH is poor in accuracy and stability, the results of KGF-SPH will not be exhibited in the following sections.

Fig. 5. Temperature variations with time for monitor particle A.
6. Improved KGF-SPH modeling of natural convection in a closed square cavity

The Improved KGF-SPH with shifting particle positions is used to model natural convections in a closed square cavity at different Rayleigh numbers in this section. In order to verify our Improved KGF-SPH formulation, the Improved KGF-SPH results are compared with the corresponding SPH and FVM simulation results.

6.1. Physical model

Schematic diagram for natural convection in a closed square cavity is provided in Fig. 6. The computational domain is a square cavity with a side length of L, both the upper and lower horizontal walls are adiabatic, the left and right vertical walls are isothermal, maintained respectively at the maximum temperature TH and the minimum temperature TC. Throughout the simulations, gravity is in negative y direction and Boussinesq approximation is used. The Boussinesq approximation means that the density differences are confined to the buoyancy term gβT(T − T0), where g represents the gravitational acceleration, βT is the coefficient of thermal expansion, and the reference temperature T0 = (TH + TC)/2.

Fig. 6. Schematic diagram for natural convection in a closed square cavity.

Particle distribution for natural convection in a closed square cavity is shown in Fig. 7, in which fluid particles are uniformly distributed in the computational domain, and virtual particles are fixed on the boundaries. The smoothing length is h = 1.3Δ, where Δ is the particle spacing, and the time step is dt = 5 × 10−6 s.

Fig. 7. Particle distribution for natural convection in a closed square cavity.

Natural convection in a closed square cavity is studied at Ra = 104, 105 and 106 to validate the Improved KGF-SPH. In this case, the Prandtl number Pr = μ/(ρ α) = 0.71, the dynamic viscosity coefficient μ = 1.707 × 10−5 kg/m·s, density ρ = 1.225 kg/m3, the thermal diffusion coefficient α = 1.963× 10−5 m2/s, the thermal expansion coefficient βT = 4.095 × 10−3 K−1. TH = 283 K, TC = 273 K, and the initial temperature of the fluid inside the square cavity is T0. The reference density ρ∞ in state equation is set to be 1.225 kg/m3, and for convenience, the artificial sound speed c values are set to be 0.25 m/s, 0.4 m/s and 0.8 m/s for Ra = 104, 105, and 106 respectively. In this paper, the size of Rayleigh number Ra is adjusted by changing the sizes of g and L. In the numerical simulation of natural convection in a closed square cavity, shifting particle position is adopted to improve the numerical stability.

6.2. Boundary condition implementation

There are two kinds of boundary conditions in natural convection problems: adiabatic boundaries and isothermal boundaries. In this paper, we use the projecting method proposed by Huang et al.[33] to calculate physical properties of virtual particles. The projecting method first finds out the normal direction nvp of all virtual particles’ position vector rvp, and extends virtual particles by an increment η Δ into the flow field along the normal direction nvp. Then we can obtain new points located on rpp, which are the projecting points corresponding to the virtual particles. η is an adjustable parameter, Δ is the initial particle spacing, the subscripts vp and pp represent virtual particles and projecting points respectively. In order to understand the projecting method, the value of η is given through four specified virtual particles A, B, C, and D on each side as shown in Fig. 8.

Fig. 8. Boundary treatment.
6.2.1. Adiabatic boundaries

The adiabatic boundary condition is a Neumann-type boundary condition with ∂T/∂n = 0, where n is the normal direction of the wall. On the adiabatic boundaries, the position vectors of virtual particles and projecting points satisfy the following relations:

where x and y represent the components of the position vector. The principle of selecting η value is that the distances of projecting points to the walls are all Δ/2. For example, as shown in Fig. 8, the corresponding projecting point of particle A is located on point M, and the corresponding projecting point of particle B is located on point N, thus the value of η is −1.5 and 3.5 respectively. After finding the projecting points, the physical properties of virtual particles are calculated by the following equations:

where j is the neighboring particle of projecting point pp, only fluid particles are involved. The pressure of virtual particles pvp is calculated by Eq. (35).

6.2.2. Isothermal boundaries

The isothermal boundary condition is a Dirichlet-type boundary condition. On the isothermal boundaries, the position vectors of virtual particles and projecting points satisfy the following relations:

In Eq. (46), the principle of selecting η value is that the distances of projecting points to the walls are all Δ/2. For example, as shown in Fig. 8, the corresponding projecting point of particle C is located on point E, and the corresponding projecting point of particle D is located on point F, thus the value of η is 4.5 and –2.5 respectively. The physical properties of virtual particles are solved by the following equations:

where j is the neighboring particle of projecting point pp, only fluid particles are involved, TW is the temperature of the walls, TW = TH on the left vertical wall, TW = TC on the right vertical wall. The pressure of virtual particles pvp is calculated by Eq. (35).

6.3. Analysis of the Numerical results
6.3.1. Natural convection patterns

For natural convection in a closed square cavity with Ra = 104, g = 8.350 m/s2, L = 0.02 m, 149×149 fluid particles are evenly placed in the computational domain. Figures 9–11 show the temperature and velocity contours at t = 4.5 s, obtained by (a) FVM, (b) SPH, and (c) Improved KGF-SPH, respectively. In Fig. 9, the temperature contours near the adiabatic walls are nearly vertical, and in Figs. 10 and 11, there are two eddies in the velocity contours. It can be seen from these figures that the SPH and Improved KGF-SPH results accord well with the FVM results, so both the SPH and Improved KGF-SPH can reasonably simulate the natural convection in a closed square cavity with Ra = 104.

Fig. 9. Temperature T contours for Ra = 104 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
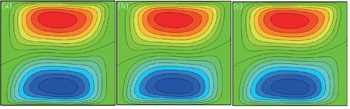Fig. 10. Horizontal velocity u contours for Ra = 104, obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
Fig. 11. Vertical velocity v contours for Ra = 104, obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.

The simulations for Ra = 105 are performed with 149×149 fluid particles, g = 5.344 m/s2, L = 0.05 m, and the temperature contours t t = 20 s are presented in Fig. 12. By comparison, both the SPH and Improved KGF-SPH behave similarly to temperature contours obtained by FVM. Figures 13 and 14 show the horizontal velocity u contours and vertical velocity v contours obtained using (a) FVM, (b) SPH and (c) Improved KGF-SPH at t = 20 s for the natural convection in a closed square cavity with Ra = 105. Though temperature contours obtained by SPH accord well with that of FVM, the velocity contours obtained by SPH are poor in stability. As shown in Figs. 13 and 14, the horizontal velocity contours obtained by using SPH are not smooth near the left wall nor right wall, and the vertical velocity contours are not smooth near the upper wall nor lower wall, while the Improved KGF-SPH results are very smooth and in good agreement with those of FVM.

Fig. 12. Temperature T contours for Ra = 105 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
Fig. 13. Horizontal velocity u contours for Ra = 105 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
Fig. 14. Vertical velocity v contours for Ra = 105 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.

For Ra = 106, g = 6.680 m/s2, L = 0.1 m, the boundary layer becomes thinner with Rayleigh number increasing, so more particles (199×199 fluid particles) are used to model the natural convection in a closed square cavity. Figure 15 displays a comparison among temperature contours at t = 30 s, obtained by using (a) FVM, (b) SPH, and (c) Improved KGF-SPH. Both the SPH and Improved KGF-SPH results accord well with that of FVM. The corresponding horizontal velocity u and vertical velocity v contours are depicted in Figs. 16 and 17 respectively. In Figs. 16 and 17, the velocity contours obtained by SPH and Improved KGF-SPH are similar to those of FVM, but the SPH results are not smooth and oscillatory near the walls and in the center of the square cavity, but the Improved KGF-SPH results are still very smooth and in good agreement with those obtained by FVM.

Fig. 15. Temperature T contours for Ra = 106 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
Fig. 16. Horizontal velocity u contours for Ra = 106 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.
Fig. 17. Vertical velocity v contours for Ra = 106 obtained by different methods: (a) FVM, (b) SPH, and (c) Improved KGF-SPH.

There are two distinct flow patterns for natural convection in a closed square cavity: heat conduction and heat convection. It can be seen from Figs. 9, 12, and 15 that as Ra increases, the interior temperature contours become more and more horizontal, since the heat convection dominates the higher-Ra range. Nevertheless, the contours near the adiabatic boundaries are normal to the horizontal walls. In Figs. 10, 13, and 16 for the horizontal velocity contours, there are two horizontal eddies: for higher Ra, these two eddies move closer to the adiabatic walls. Similarly, two vertical eddies are visible in the vertical velocity contours (Figs. 11, 14, and 17), and they move closer to the isothermal walls.

It can be seen from Fig. 9–17 that as Ra number increases, the boundary layer becomes thinner, and the flow inside the cavity becomes more and more complex. The temperature contours obtained by using the SPH and Improved KGF-SPH are in good agreement with that of FVM, so both the SPH and the Improved KGF-SPH can simulate the temperature field for the natural convection exactly. However, the velocity contours obtained by using the SPH become poorer for higher Ra, especially when Ra = 106, but the Improved KGF-SPH results are in good agreement with FVM results. To sum up, the stability of the Improved KGF-SPH is better than SPH.

6.3.2. Velocity profiles

In order to validate the accuracy of Improved KGF-SPH, the velocity profiles obtained by SPH and Improved KGF-SPH are compared with those of FVM. For convenience, the dimensional variables are non-dimensionalized by the following equations: x* = x/L, y* = y/L, u* = uL/α, v* = vL/α. The non-dimensional horizontal velocity u* distribution along the mid-width (x = L/2) and non-dimensional vertical velocity v* along mid-height (y = L/2) over the Ra range of 104 to 106 are presented in Figs. 18(a) and 18(b) respectively. Partial enlarged drawing of Ra = 106 is also presented in Fig. 18(b) to show the difference between these methods. It can be seen from Fig. 18(a) that there is excellent agreement among the SPH, Improved KGF-SPH, and FVM results for Ra = 104 and 105, but when Ra = 106, there is a large error between SPH and FVM results while the Improved KGF-SPH results are still close to the FVM results. In Fig. 18(b), there is a good congruence among the SPH, Improved KGF-SPH, and FVM results, even for high Rayleigh numbers, but from the partial enlarged drawing of Ra = 106, we can see that the maximum non-dimensional vertical velocity obtained using Improved KGF-SPH is closer to FVM results than that of SPH. In general, Improved KGF-SPH is more accurate than SPH for modeling natural convection in a closed square cavity.

Fig. 18. Non-dimensional velocity profiles along central lines: (a) non-dimensional horizontal velocity u*, and (b) non-dimensional vertical velocity v*.

The maximum non-dimensional horizontal velocity along the mid-width and the maximum non-dimensional vertical velocity along the mid-height are presented in Table 1. The maximum values obtained by de Vahl Davis[35] and Wan et al.[36] are also summarized in Table 1. The results of de Vahl Davis are taken as the benchmark in this paper, errors between the benchmark and the DSC, FVM, SPH, Improved KGF-SPH are also presented in Table 1. It can be seen from Table 1 that errors between DSC and the benchmark are about 1%∼4%, errors between SPH and the benchmark are about 1%∼7%, while errors between the Improved KGF-SPH and the benchmark are less than 1%, except for the maximum non-dimensional horizontal velocity at Ra = 106 with error about 2.66%, so the Improved KGF-SPH is more accurate than SPH in modeling natural convection in a closed square cavity.

Table 1.

Comparison of maximum non-dimensional velocity at central lines.

.
7. Conclusions

A new Laplacian discretization scheme is proposed to avoid bringing errors of the first derivatives to the second derivatives in the KGF-SPH kernel and particle approximation. The superiority of the new Laplacian discretization scheme applied in KGF-SPH is verified by modeling 1D and 2D heat conduction problems. The Improved KGF-SPH is successfully used to study natural convection in a closed square cavity with Ra = 104, 105, and 106. It can be seen that the SPH overestimates the heat transfer, the KGF-SPH results oscillate violently, while the Improved KGF-SPH results accord well with the analytical solution and the reference solution. The Improved KGF-SPH is more accurate than SPH and stabler than KGF-SPH, thus it is an attractive tool to study and model the heat transfer problems. In this paper, only 1D and 2D simulations are done; as a next step, our method can be extended to solving 3D heat transfer problems. Furthermore, the application of the proposed method can be broadened to other problems controlled by governing equations, such as viscous fluid flow.

Reference
1Belytschko TLu Y YGu L 1994 Int. J. Numer. Method Eng. 37 229
2Wang J FSun F XCheng R J 2010 Chin. Phys. B 19 060201
3Cheng R JCheng Y M 2011 Chin. Phys. B 20 070206
4Wang J FCheng Y M 2012 Chin. Phys. B 21 120206
5Wang J FCheng Y M 2013 Chin. Phys. B 22 030208
6Wang J FBai F NCheng Y M 2011 Chin. Phys. B 20 030206
7Liu W KJun SLi SZhang Y F 1995 Int. J. Numer. Method Fluids 20 1081
8Chen LCheng Y M 2010 Chin. Phys. B 19 090204
9Weng Y JCheng Y M 2013 Chin. Phys. B 22 090204
10Yang X FLiu M B2012Acta Phys. Sin.61224701(in Chinese)
11Lei J MYang HHuang C 2014 Acta Phys. Sin. 63 224701 (in Chinese)
12Koshizuka SOja Y 1996 Nucl. Sci. Eng. 123 421
13Chen J KBeraun J ECarney T C 1999 Int. J. Numer. Method Eng. 46 231
14Liu G RLiu M B2003Smoothed particle hydrodynamics: a meshfree particle methodSingaporeWorld Scientific1200ISBN: 0849312388
15Lucy C B 1977 Astron. J. 82 1013
16Gingold R AMonaghan J J 1977 Mon. Not. R. Astron. Soc. 181 375
17Morris J PFox P JZhu Y 1997 J. Comput. Phys. 136 214
18Monaghan J JKocharyan A 1995 Comput. Phys. Commun. 87 225
19Jeong J HJhona M SHalowb J Svan Osdol J 2003 Comput. Phys. Commun. 153 71
20Bonet JKulasegaram SRodriguez-Paz M XProfit M 2004 Comput. Methods Appl. Mech. Eng. 193 1245
21Gong KLiu HWang B L 2009 J. Hydrodyn. 21 750
22Ming F RSun P NZhang A M 2014 Appl. Math. Mech. 35 453
23Danis M EOrhan MEcder A 2013 Int. J. Comput. Fluid D 27 15
24Cleary P W 1998 Appl. Math. Model. 22 981
25Chaniotis A KPoulikakos DKoumoutsakos P 2002 J. Comput. Phys. 182 67
26Szewc KPozorski JTanièere A 2011 Int. J. Heat Mass Transfer 54 4807
27Swegle J WHicks D LAttaway S W 1995 J. Comput. Phys. 116 123
28Nestor RBasa MQuinlan N20083rd ERCOFTAC SPHERIC workshop on SPH applicationsJune 4–6, 2008Lausanne, Switzerland109
29Xu RStansby PLaurence D 2009 J. Comput. Phys. 228 6703
30Hashemi M RFatehi RManzari M T 2012 Int. J. Non-Linear Mech. 47 626
31Liu M BXie W PLiu G R 2005 Appl. Math. Model. 29 1252
32Zhang G MBatra R C 2004 Comput. Mech. 34 137
33Huang CLei J MLiu M BPeng X Y 2015 Int. J. Numer. Method Fluids 78 691
34Monaghan J J 2005 Rep. Prog. Phys. 68 1703
35de Vahl Davis G 1983 Int. J. Numer. Method Fluids 3 249
36Wan D CPatnaik B S VWei G W 2001 Numer. Heat Transfer B-Fund. 40 199