Cite this Article
Yang Yong-Ge, Xu Wei, Sun Ya-Hui, Gu Xu-Dong. Stochastic response of van der Pol oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. Chinese Physics B, 2016, 25(2): 020201  
Permissions
Stochastic response of van der Pol oscillator with two kinds of fractional derivatives under Gaussian white noise excitation
Yang Yong-Ge1, Xu Wei1, †, , Sun Ya-Hui2, Gu Xu-Dong3
Department of Applied Mathematics, Northwestern Polytechnical University, Xi'an 710072, China
State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi'an Jiaotong University, Xi'an 710049, China
Department of Engineering Mechanics, Northwestern Polytechnical University, Xi'an 710129, China

 

† Corresponding author. E-mail: weixu@nwpu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11472212, 11532011, and 11502201).

Abstract
Abstract

This paper aims to investigate the stochastic response of the van der Pol (VDP) oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. First, the fractional VDP oscillator is replaced by an equivalent VDP oscillator without fractional derivative terms by using the generalized harmonic balance technique. Then, the stochastic averaging method is applied to the equivalent VDP oscillator to obtain the analytical solution. Finally, the analytical solutions are validated by numerical results from the Monte Carlo simulation of the original fractional VDP oscillator. The numerical results not only demonstrate the accuracy of the proposed approach but also show that the fractional order, the fractional coefficient and the intensity of Gaussian white noise play important roles in the responses of the fractional VDP oscillator. An interesting phenomenon we found is that the effects of the fractional order of two kinds of fractional derivative items on the fractional stochastic systems are totally contrary.

PACS: 02.50.–r;05.40.–a;05.40.Ca;
Keyword:stochastic averaging method;fractional derivative;van der Pol;equivalent stochastic system;
1. Introduction

Fractional calculus[1–5] can be traced back to the Leibniz’s letter to L’Hospital in 1695. Unfortunately, for quite a long time, fractional calculus remained in an abstract mathematical field and developed very slowly. In the past few decades, fractional calculus has attracted considerable attention, partly due to the fact that the fractional-order mathematical models can be used to make a more accurate description than the integer-order models. Thus, fractional calculus can be considered as an old and yet novel branch of mathematics.[6,7]

Because of the extensive existence of the random factor,[8,9] it is of practical significance to study the stochastic fractional systems. In order to obtain the approximate analytical solution of fractional systems, a lot of approaches have been used by many authors. The stochastic averaging method has been used by many researchers to obtain the analytical solutions. Specifically, Huang and Jin[10] investigated the stationary response and stability of a single-degree-of-freedom (SDOF) strongly nonlinear stochastic system with light damping modeled by a fractional derivative. Chen et al.[11] and Chen and Zhu[12] studied the stationary responses. Chen and Zhu[13] investigated the stochastic jump and bifurcation. Chen et al.[14] studied first passage failure; Chen et al.[15,16] fractional control of stochastic fractional systems. Yang et al.[17,18] studied the stationary response of a nonlinear system with Caputo-type fractional derivative under Gaussian white noise excitation by the stochastic averaging method. Zhang et al.[19] discussed the response of a Duffing–Rayleigh system with fractional derivative under Gaussian white noise excitation. There are several other methods to deal with stochastic systems besides the stochastic averaging method. Spanos and Zeldin[20] put forward a frequency-domain method for systems with fractional derivatives. Agrawal[21] proposed an analytical approach for stochastic dynamic systems endowed with a fractional derivative by the eigenvector expansion method and Laplace transforms. Xu et al.[22,23] studied the response of the stochastic oscillator with fractional derivative by using a new technique based on the Lindstedt–Poincaré (LP) method and multiple-scale method. Liu et al.[24] investigated the principal resonance responses of SDOF systems with small fractional derivative damping subjected to narrow-band random parametric excitation by the multiple scale method.

However, the systems mentioned in the above literature only contain one kind of fractional derivative, little work is related to the study of deterministic or stochastic systems containing two kinds of fractional derivative to the best of the authors’ knowledge. Huang et al.[25] discussed the statistical behaviors of the response of stochastic systems endowed with two kinds of fractional derivatives by using the Laplace transform in conjunction with the weighted generalized Mittag–Leffler function. Shen et al.[26] investigated the primary resonance of the Duffing oscillator with two kinds of fractional-order derivatives. Liao[27] studied the Duffing oscillator with two kinds of fractional-order derivative by using the improved version of the constrained optimization harmonic balance method.

Inspired by the above discussion, in this paper we are to investigate the stationary response of the VDP oscillator with two kinds of fractional derivatives excited by Gaussian white noise.

The rest of this paper is organized as follows. The fractional VDP oscillator is reduced to the equivalent stochastic VDP oscillator without fractional derivative terms by using the generalized harmonic function technique in Section 2. The approximate analytical solutions of the equivalent VDP oscillator are obtained by the stochastic averaging method in Section 3. The predictor–corrector algorithm for the solution of the initial value problem with fractional derivative is briefly introduced in Section 4. Numerical simulations are performed to verify the theoretical results in Section 5. Finally, the conclusions are given in Section 6.

2. Equivalent VDP oscillator

Consider a fractional VDP oscillator[28–30] with two kinds of fractional derivatives subjected to Gaussian white noise. The motion of the system is governed by the following equation:

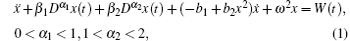
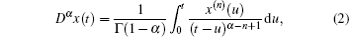
where a dot over a variable denotes differentiation with respect to timet; β1, β2, and ω are constant coefficients; W(t) is a stationary Gaussian white noise with correlation function E[W(t)W(t + τ)] = 2Dδ(τ). There are many definitions of the fractional derivative. In the present paper, the Caputo-type fractional derivative is adopted as follows:

in which n − 1 < α < n, n ∈ N, and Γ(·) is a Gamma function.

According to Refs. [11], [14], and [26], the term associated with the fractional derivative not only serves as the classical damping force, but also contributes to the restoring force. Based on the generalized harmonic function technique,[11,14] this term can be replaced by a linear restoring force and a linear damping force:

In order to obtain the values of C1 (α1), C2 (α2), K1 (α1), and K2 (α2), we first introduce two important formulae:

We can assume that the solution of the fractional VDP oscillator (1) has the following form:

First, we present the detailed derivation procedure for C1 (α1).

Using the transformations of coordinates s = t − u and d s = −d u, one can obtain

Define the first part of Eq. (9) as C11 and the second part as C12, then

Define the first part of Eq. (10) as C111 and the second part as C112, then

According to Eqs. (11)–(13), one can obtain

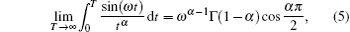
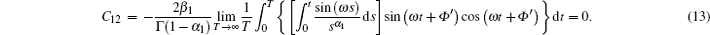
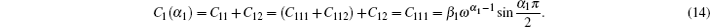
Second, we present the detailed derivation procedure for K1 (α1).

Using the transformations of coordinates s = t − u and ds = − du, one can obtain

Define the first part of Eq. (16) as K11 and the second part as K12, then

Define the first part of Eq. (16) as K121 and the second part as K122, then

According to Eqs. (17), (19), and Eq. (20), one can obtain

According to Eqs. (14) and (21), one can obtain

Similarly, one could also obtain C2 (α2), K2 (α2):

Thus

Therefore, the equivalent VDP oscillator associated with system (1) is given by

in which

3. Stochastic averaging

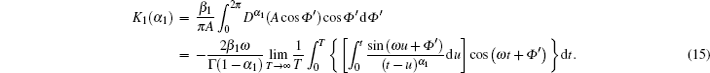
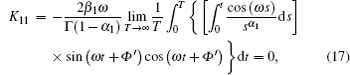
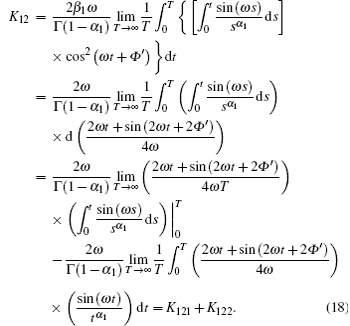
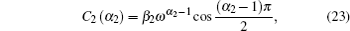
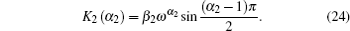
In this section, the stochastic averaging method is applied to the VDP oscillator (26).

According to Ref. [20], we can assume that the solution of system (26) has the following form:

where A, Φ, and Θ are random processes. One can obtain the following equations for the amplitude A and the phase angle Θ:

where

According to the Stratonovich–Khasminskii theorem, A(t) and Φ(t) converge weakly into a two-dimensional diffusion Markov process as ε → 0, in a time interval 0 ≤ t ≤ T, where T ∼ O(ε−1). Equation (30) shows that the averaged Itô equation for A(t) is independent of Θ (t), the limiting process A(t) is a one-dimensional diffusion process governed by

where the drift and diffusion coefficients, respectively, are

Then substituting Eq. (31) into Eq. (33), the explicit expression for the averaged drift and diffusion coefficients can be obtain as follows:

in which

The corresponding FPK equation associated with Eq. (29) has the following form:

The boundary conditions are p = c in which c ∈ (−∞, +∞) at A = 0 and p → 0, ∂ p/∂ A → 0 as A → ∞. Thus, based on these boundary conditions, the stationary solution of Eq. (37) is

where C is the normalization constant.

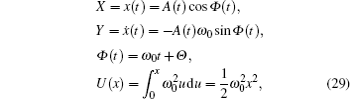
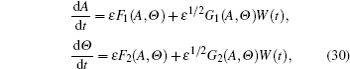
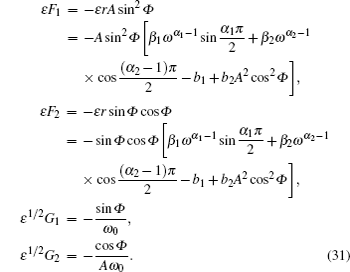
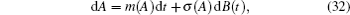
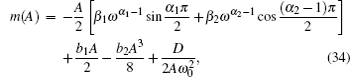
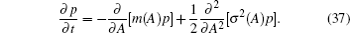
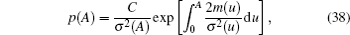
The stationary probability density of the system Hamiltonian can be obtained from Eq. (38) as follows:

Then the joint stationary probability density of the displacement and velocity can be obtained as follows:

where

4. Numerical simulation

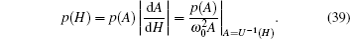
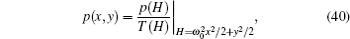
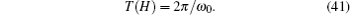
In the paper, the following algorithm[31] is used to deal with the numerical solution of differential equations of fractional order, equipped with suitable initial conditions, i.e.,

Based on the predictor–corrector algorithm, the following iterative formula is adopted:

in which the weight of the corrector ai,n+1 is in the following form:

where denotes the predicted value, which is governed by

bi,n+1 represents the weight of the predictor and is expressed as

The error of this approach is estimated to be O(hmin(2,1+α)). The pseudo-code is available in the appendix of Ref. [31].

5. Numerical results

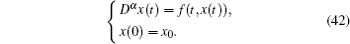
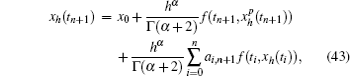
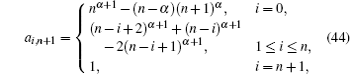
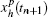
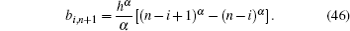
In order to demonstrate the efficiency of the proposed method, some numerical results are obtained for the fractional VDP oscillator (1) with different parameter values. It is found that the analytical results and the Monte Carlo simulations of the original VDP oscillator are in satisfactory agreement with each other. We also discuss the effects of fractional order α1 and α1, the fractional coefficients β1 and β2, and the intensity of Gaussian white noise on the fractional VDP oscillator.

In this section, the time step is 0.01 and the total computation time is 104 s in the implementation of the Monte Carlo simulation. The results from the analytical solutions and the Monte Carlo simulations are shown in the following figures by solid line (—) and star (*), respectively.

5.1. Effect of fractional order α1 ∈ (0,1)

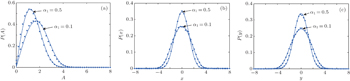
We examine the effect of the order of Caputo-type fractional derivative α1 on the fractional VDP oscillator (1). The stationary probability density of amplitude p(A), displacement p(x), and velocity p(y) from an analytical solution for different values of the fractional derivative order are shown in Figs. 1 and 2. The results from Monte Carlo simulation of the original system (1) are shown in Figs. 1 and 2. Examining those figures, it is found that the analytical results and the Monte Carlo simulations are in very satisfactory agreement with each other. We can conclude that the smaller the fractional derivative order α1, the greater the probability of the oscillator with large amplitude (displacement or velocity) is.

Fig. 1. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α2 = 1.7, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
Fig. 2. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α2 = 1.8, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
5.2. Effect of fractional order α2 ∈ (1,2)

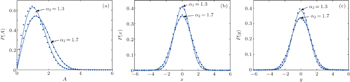
We examine the effect of the order of Caputo-type fractional derivative α2 on the fractional VDP oscillator (1). The results from the analytical solution and the Monte Carlo simulation are shown in Figs. 3 and 4. Examining those figures, it is found that the analytical results and the Monte Carlo simulations are in good agreement with each other. We can obtain the following interesting conclusion, i.e., the smaller the fractional derivative order α2, the smaller the probability of the oscillator with large amplitude (displacement or velocity) is, which is totally contrary to the conclusion in Subsection 5.1.

Fig. 3. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
Fig. 4. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.5, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
5.3. Effect of fractional coefficient β1

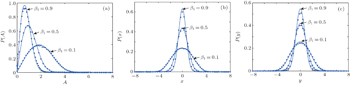
We investigate the effect of the coefficient of Caputo-type fractional derivative β1 on the fractional VDP oscillator (1). The results from the analytical solution and the Monte Carlo simulation are shown in Figs. 5 and 6. Those figures show very satisfactory agreement between the analytical results and the Monte Carlo simulations. We can obtain the following conclusions: the smaller the fractional coefficient β1, the larger the probability of the oscillator with large amplitude (displacement or velocity) is.

Fig. 5. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, α1 = 1.7, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
Fig. 6. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.6, α1 = 1.8, β2 = 0.2, b1 = b2 = 0.05, ω = 1.0, and D = 0.4.
5.4. Effect of fractional coefficient β2

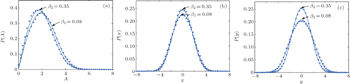
Now we come to examine the effect of the coefficient of Caputo-type fractional derivative β2 on the fractional VDP oscillator (1). The results from the analytical solution and the Monte Carlo simulation are shown in Figs. 7–9. Examining those figures shows very satisfactory agreement between the analytical results and the Monte Carlo simulations. We can obtain the following conclusion: the smaller the fractional coefficient β2, the larger the probability of the oscillator with large amplitude (displacement or velocity) is, which is the same as the conclusion in Subsection 5.3.

Fig. 7. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, α1 = 1.7, β1 = 0.3, b1 = b2 = 0.05, ω = 1.0, and D = 0.2.
Fig. 8. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, α1 = 1.7, β1 = 0.3, b1 = b2 = 0.05, ω = 1.0, and D = 0.6.
Fig. 9. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, α1 = 1.7, β1 = 0.3, b1 = b2 = 0.05, ω = 1.0, and D = 0.9.
5.5. Effect of the intensity D

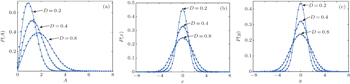Finally, we consider the effect of the intensity of Gaussian white noise D on the fractional VDP oscillator (1). The results from the analytical solution and the Monte Carlo simulation are shown in Figs. 10 and 11. Examining those figures indicates very satisfactory agreement between the analytical results and the Monte Carlo simulations. We can obtain the following conclusions: the smaller the intensity of Gaussian white noise D, the smaller the probability of the oscillator with large amplitude (displacement or velocity) is.

Fig. 10. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.4, α1 = 1.7, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, and ω = 1.0.
Fig. 11. Stationary probability densities of amplitude A, displacement x, and velocity y of oscillator (1) with α1 = 0.5, α1 = 1.7, β1 = 0.3, β2 = 0.2, b1 = b2 = 0.05, and ω = 1.0.
6. Conclusions

In this paper, we investigate the stochastic response of VDP oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. The equivalent VDP oscillator without fractional derivative terms for the fractional VDP oscillator is obtained by using the generalized harmonic balance technique. Then, the analytical solution of the equivalent VDP oscillator can be derived by the stochastic averaging method. Finally, the analytical results are validated by those from the Monte Carlo simulation of the original fractional VDP oscillator.

The numerical results not only demonstrate the accuracy of the proposed approach but also show that the fractional orders α1 and α2, the fractional coefficients β1 and β2 and the intensity D of Gaussian white noise play important roles in the responses of the fractional VDP oscillator.

More specifically, the smaller the fractional derivative order α1, the greater the probability of the oscillator with large amplitude (displacement or velocity) is; the effect of fractional order α2 is contrary to that of fractional order α1, i.e., the smaller the fractional derivative order α2, the smaller the probability of the oscillator with large amplitude (displacement or velocity) is. The smaller the fractional coefficient β1 or β2, the larger the probability of the oscillator with large amplitude (displacement or velocity) is. The smaller the intensity D of Gaussian white noise, the smaller the probability of the oscillator with large amplitude (displacement or velocity) is.

It is noted that the approach is only suitable for the fractional VDP oscillator with two kinds of fractional derivatives subjected to weakly Gaussian white noise and light damping.

Reference
1Oldham K BSpanier J1974The Fractional Calculus-Theory and Applications of Differentiation and Integration to Arbitrary OrderNew YorkAcademic Press1
2Podlubny I1999Fractional Differential EquationsLondonAcademic Press10
3Shen Y JYang S PXing H J2012Acta Phys. Sin.61110505(in Chinese)
4Shen Y JYang S PXing H J2012Acta Phys. Sin.61150503(in Chinese)
5Wei PShen Y JYang S P 2014 Acta Phys. Sin. 63 010503 (in Chinese)
6Machado J TKiryakova VMainardi F 2011 Commun. Nonlinear Sci. Numer. Simul. 16 1140
7Li C PDeng W HXu D 2006 Physica A 360 171
8Li CXu WWang LLi D X 2013 Chin. Phys. B 22 110205
9Huang D MXu WXie W XHan Q 2015 Chin. Phys. B 24 040502
10Huang Z LJin X L 2009 J. Sound Vib. 319 1121
11Chen L CWang W HLi Z SZhu W Q 2013 Int. J. Non-Linear Mech. 48 44
12Chen L CZhu W Q 2009 Nonlinear Dyn. 56 231
13Chen L CZhu W Q 2011 Int. J. Non-Linear Mech. 46 1324
14Chen L CLi Z SZhuang Q QZhu W Q 2013 J. Vib. Control 19 2154
15Chen L CHu FZhu W Q 2013 Fract. Calc. Appl. Anal. 16 189
16Chen L CZhao T LLi WZhao J 2015 Nonlinear Dyn first online 5 September 2015
17Yang Y GXu WJia W THan Q 2015 Nonlinear Dyn. 79 139
18Yang Y GXu WGu X DSun Y H 2015 Chaos, Solitons and Fractals 77 190
19Zhang R RXu WYang G DHan Q 2015 Chin. Phys. B 24 020204
20Spanos PZeldin B 1997 J. Eng. Mech. 123 290
21Agrawal O P 2004 J. Vib. Acoust. 126 561
22Xu YLi Y GLiu D 2014 J. Comput. Nonlinear Dyn. 9 031015
23Xu YLi Y GLiu DJia W THuang H 2013 Nonlinear Dyn. 74 745
24Liu DLi JXu Y 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3642
25Huang Z LJin X LLim C WWang Y 2010 Nonlinear Dyn. 59 339
26Shen Y JYang S PXing H JGao G S 2012 Commun. Nonlinear Sci. Numer. Simul. 17 3092
27Liao H2014Nonlinear Dyn.791311
28Shen Y JYang S PSui C Y 2014 Chaos, Solitons and Fractals 67 94
29Liu X JHong LYang L X 2014 Abstr. Appl. Anal. 2014 835482
30Wei PShen Y JYang S P 2014 Acta Phys. Sin. 63 010503 (in Chinese)
31Diethelm KFord N JFreed A D 2002 Nonlinear Dyn. 29 3