† Corresponding author. E-mail:
Project supported by the National High Technology Research and Development Program of China (Grant No. 2015AA034201), the National Natural Science Foundation of China (Grant Nos. 11234013 and 11264014), the Natural Science Foundation of Jiangxi Province, China (Grant Nos. 20133ACB21010 and 20142BAB212002), and the Foundation of Jiangxi Education Committee, China (Grant Nos. GJJ14254 and KJLD14024). C. Y. Ouyang is also supported by the “Gan-po talent 555” Project of Jiangxi Province, China.
The physics of ionic and electrical conduction at electrode materials of lithium-ion batteries (LIBs) are briefly summarized here, besides, we review the current research on ionic and electrical conduction in electrode material incorporating experimental and simulation studies. Commercial LIBs have been widely used in portable electronic devices and are now developed for large-scale applications in hybrid electric vehicles (HEV) and stationary distributed power stations. However, due to the physical limits of the materials, the overall performance of today’s LIBs does not meet all the requirements for future applications, and the transport problem has been one of the main barriers to further improvement. The electron and Li-ion transport behaviors are important in determining the rate capacity of LIBs.
Lithium-ion batteries (LIBs) have the best comprehensive performance of the currently commercialized secondary battery systems, due to high energy density, long cycling life, non-toxicity, non-pollution, flexibility, and lightweight design. [ 1 ] Nowadays, LIBs are widely used to supply power for portable electronic devices. With the ever-increasing demand for energy conversion and storage devices in new industries like electric vehicles (EV), the performance of the LIBs required by industry becomes very strict. In addition to higher energy density and better safety, the rate capability is emphasized in the EV industry because it directly determines the charging and discharging speed of the batteries. From the physical point of view, the rate capability of the LIBs is strongly associated with the ionic and electronic conduction in electrode materials.
The electrochemical reaction occurring in electrode materials in LIBs includes two kinetic behaviors in the charging and discharging process: (i) Li-ion insertion and extraction; (ii) electron/charge transfer upon Li insertion and extraction induced in the process of oxidation or reduction of the electrode materials. In the process of the electrochemical reaction in electrodes, Li-ion distributions at the surface and inside the electrode differ, which manifests as a Li-ion concentration gradient and drives Li-ion diffusion. In most cases, Li diffusion plays an import role in the kinetic process that occurs in the electrode materials, because the diffusion determines the reaction velocity of electrode materials and thus the rate performance of the electrode. [ 2 , 3 ]
Both cathode and anode materials are mixed ionic and electronic conductors. Electronic conduction performance can be improved by enhancing the intrinsic electronic conductivity or by other technical strategies like carbon coating, adding a conduction additive, etc. [ 4 ] For ionic conduction, the intrinsic ionic conductivity is the key factor. It is intrinsically difficult to improve ionic conduction, as the ionic transport is strongly related with the structure and composition of the material. On the other hand, although technically decreasing the particle size of electrode materials and then shortening Li-ion migration paths can improve the rate capability, [ 5 ] it simultaneously increases the specific surface area of electrode materials, which causes new stability problems related to the surface or interface.
In recent years, more and more research is focused on the transport mechanism of the charge carriers in lithium batteries, both experimentally and theoretically. [ 6 – 9 ] Understanding the transport mechanism helps researchers find ways to improve the relatively low electrical or ionic conductivity of LIB materials. In this paper, we review the kinetic behavior of electrons and ions in electrode materials for LIBs and summarize the current status of research in the literature.
Ionic transport is associated with the macroscopic diffusion and microscopic migration behavior of ions under the influence of various gradient forces such as concentration gradient, chemical potential gradient, and electric field gradient. The diffusion process can be described by Fick’s law of diffusion: [ 10 ]
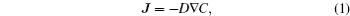
Fick’s law describes the diffusion process from the macroscopic aspect; other factors besides concentration are considered in the chemical diffusion coefficient D . From the microscopic point of view, according to statistical physics, the self-diffusion coefficient is more reasonable to reveal the intrinsic nature of the Li-ion migration. According to transition state theory, [ 11 , 12 ] the self-diffusion coefficient ( D *) can be calculated through the following formula:

Another commonly used quantity to characterize ion motion is the tracer-diffusion coefficient ( D ), which is defined as [ 11 ]

Although the Li-ion diffusion coefficient is generally accepted to describe diffusion behavior, ionic conductivity is also widely used to describe the motion of Li ions under external electrical potential. The relationship between ionic conduction and the diffusion coefficient can be described by the Nernst–Einstein equation [ 15 ]
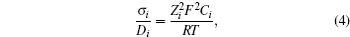

From the microscopic viewpoint, diffusion is characterized by the Brownian motion of atoms or molecules. In solid materials, the amplitude of a particle’s vibration near its equilibrium position at a given temperature is smaller than that at its melting point. The thermal energy gives a certain driving force to make the atoms deviate from their equilibrium positions, the atoms have a certain probability to overcome the energy barrier, and then migration occurs. For an atom (ion) to make such a movement, two conditions must be met: (i) an adjacent site must be empty, and (ii) the atom must have sufficient energy to break bonds with its neighbor atoms and then cause some lattice distortion during the displacement. Generally, diffusion in solids can be classified into two categories: vacancy mechanism and non-vacancy mechanism. In LIBs materials, the diffusion mechanism is more complex and other factors should also be included when we analyze Li-ion diffusion.
Without vacancy in the lattice, interstitial diffusion is very important. Interstitial diffusion involves atoms that migrate from one interstitial position to a neighboring one that is empty. For example, the diffusion of the charge carrier ions (Li + , Na + , Ag + , K + , Rb + , Cs + ) in β -Al 2 O 3 [ 17 ] is in the interstitial mechanism. The transport process of the interstitial mechanism is shown in Fig.
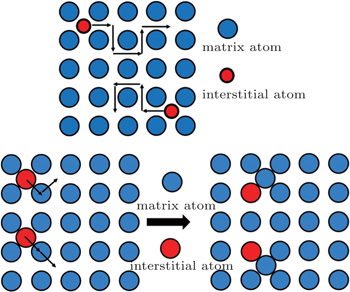 | Fig. 1. Interstitial diffusion mechanism. (a) Direct interstitial diffusion. (b) Knock-off migration mechanism. [ 18 ] |
Comparable to the direct interstitial mechanism, there is the indirect interstitial mechanism. In this case, the size of the interstitial atoms can be the same as the host matrix atoms. These atoms push their neighboring matrix atoms away, into adjacent interstitial sites, and replace them, as shown in Fig.
Atoms can also migrate in a collective manner, which involves the simultaneous motion of several atoms in substitutional solid solutions, in which solute atoms are similar in size to the matrix atoms. The diffusion can be classified into two simple categories: direct exchange mechanism and ring mechanism, as shown in Fig.
 | Fig. 2. Direct exchange and ring diffusion mechanism. [ 18 ] |
When vacancies are available, vacancy-assisted diffusion is much easier than the non-vacancy diffusion. The vacancy diffusion mechanism involves the exchange of an atom from a normal lattice site to an adjacent vacancy, as shown in Fig.
 | Fig. 3. Vacancy diffusion mechanism. [ 18 ] |
Vacancy diffusion dominates the Li diffusion in most electrode materials. On one hand, many Li vacancies are created in the electrode material upon charging (Li removal) of the electrode. On the other hand, the lattice change to the electrode material is rather small upon Li insertion/extraction, which is a general requirement for electrodes of LIBs. Therefore, vacancy diffusion in the electrode materials is much easier than interstitial diffusion. Lithium diffusion in all cathode materials is related with the vacancy mechanism. The concentration of vacancies is important to the Li migration pathway and the energy barrier. For example, Li diffusion pathways and energy barriers in LiCoO 2 cathodes are different for mono-vacancy and divacancy. [ 24 , 25 ]
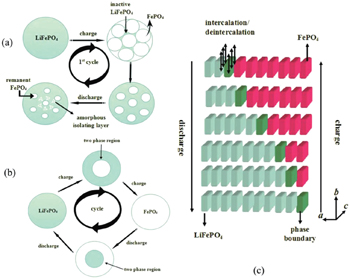
In some LIB materials, clear phase separations and two-phase coexistence may occur during the charging/discharging process. In those cases, the Li migration behavior near the phase boundary is very important. As an example, the LiFePO 4 phase changes into the FePO 4 phase upon Li removal, and a clear LiFePO 4 /FePO 4 phase boundary is formed in this process. Lithium diffusion behavior in these materials can be monitored through the movement of the phase boundary from the macroscopic point of view. The diffusion behavior with this mechanism clearly differs from those in solid solution materials.
The phase boundary movement mechanism for LiFePO 4 was first proposed by padihi et al ., [ 26 ] and now has been extensively discussed in the literature. [ 27 – 32 ] Three typical models are proposed, as shown in Fig.
Experimentally, Lithium’s chemical diffusion coefficient can be measured using electrochemical techniques. Several methods, such as electrochemical impedance spectroscopy (EIS), [ 37 , 38 ] the potentiostatic intermittent titration technique (PITT), [ 39 ] the galvanostatic intermittent titration technique (GITT), [ 40 ] and the potential step chrono-amperometry (PSCA), [ 41 , 42 ] can be used to study the Li diffusion kinetics and to estimate the chemical diffusion coefficients in solid electrodes. These measurement techniques have been widely applied to electrode materials. The measurements of the chemical diffusion coefficient for several typical electrode materials are summarized in Table
| Table 1. Chemical diffusion coefficient of Li ions in different electrode materials. . |
Atomic scale simulation of Li diffusion is one way to understand the Li diffusion mechanism in electrodes in detail from the microscopic point of view. Computer simulation, especially first-principles calculation, [ 58 – 61 ] is a powerful tool for understanding atoms’ diffusion in an electrode at the microscopic level.
Many published studies of lithium diffusion in LIB materials used Monte Carlo (MC) simulations. For example, combining kinetic MC simulations with first-principles calculations, Van et al . [ 24 , 61 , 62 ] calculated the Li diffusion coefficient in Li x CoO 2 with a Li concentration of 0 ≤ x < 1. They found that Li diffusion in this compound occurs predominantly by a divacancy mechanism, and the activation energy barrier for the divacancy migration strongly depends on the Li concentration. Ouyang et al . [ 63 , 64 ] investigated Li diffusion behavior in Li x Mn 2 O 4 by MC simulation, in which the MC step is imbued with real meaning of time through a comparison with specifically designed experiments. With a real time step, the Li flux can be directly converted into current density, from which the Li-ion conductivity can be calculated via Ohm’s law. The same method was also shown to correctly predict the Li diffusion behavior in LiFePO 4 materials. [ 65 ]
Another powerful tool that is widely used to study the Li diffusion behavior in LIB materials is ab initio molecular dynamics (AIMD). [ 66 – 69 ] Little classical MD simulation of Li migration in electrode materials is reported in the literature because of the difficulty in figuring out a reliable potential to describe the inter-atomic interactions. [ 70 , 71 ] In contrast, ab initio calculation can correctly reproduce the inter-atomic interaction, and therefore AIMD can give a correct description of the Li diffusion behavior in solid materials. Ouyang et al . [ 72 ] investigated the Li dynamics in the spinel LiMn 2 O 4 compound from AIMD calculations. They found that the energy barrier of Li monovacancy migration is about 0.23 eV and 0.61 eV in LiMn 2 O 4 and Li 0.5 Mn 2 O 4 , respectively. With a selective AIMD simulation within the adiabatic trajectory approximation, they also identified the one-dimensional (1D) Li diffusion pathway in the LiFePO 4 cathode. [ 73 ] In addition, Johari et al. [ 74 ] studied the diffusion kinetics during the lithiation process of crystalline as well as amorphous Si anodes using ab initio finite temperature MD. They found that the diffusivity of Li is 10 times faster in amorphous Si (∼10 −8 cm 2 ·s −1 ) than in crystalline Si (∼10 −9 cm 2 ·s −1 ). Moreover, the diffusivity of Si is 2 orders of magnitude slower than Li in amorphous Si, while 4 orders of magnitude slower in crystalline Si. As a consequence, their results reveal that Li has to penetrate the anode by pushing out the Si atoms, generating stress, and the faster diffusion of Si in amorphous Si helps mitigate the large diffusion-induced stress in Si anodes.
First-principles calculations combined with the NEB technique provide another approach to studying Li diffusion in LIB materials in a more microscopic manner. The NEB method optimizes the Li migration pathway and calculates the Li migration energy barrier from the atomic scale, which provides a better understanding of the Li migration mechanism. Recently, many papers have reported on Li diffusion behavior in LIB materials in the literature. [ 75 – 77 ] For example, using the NEB method, Chen et al . [ 19 ] studied the Li diffusion mechanism in Li 4+ x Ti 5 O 12 anodes. They demonstrated that Li migration in the discharged state Li 4 Ti 5 O 12 is dominated by the vacancy mechanism, while cooperative migration (knock-off mechanism) is dominant in the lithiated state Li 7 Ti 5 O 12 . With the same methodology, Xu et al . [ 78 ] investigated Li diffusion in graphite. Their results show that the Li migration is sensitive to the stacking mode of the graphite and that A–B stacking results in a higher migration energy barrier than A–A stacking. Similar studies have also been carried out to investigate Li migration in graphene [ 79 ] and silicone. [ 80 ] After the Li migration energy barrier is obtained, it is convenient to evaluate the self diffusion coefficient through transition state theory [ 12 ] and the lattice gas model, [ 81 ] as given by Eq. (
Temperature is the most profound influence on diffusion behavior. No matter which diffusion mechanism, diffusion as a function of temperature always obeys the Arrhenius formula [ 86 ]

As discussed above, electrode materials should be mixed ionic-electronic conductors. Therefore, the Li-ion migration interacts with electron transfer in solid materials; i.e., electron transfer influences Li-ion diffusion. [ 89 ] The chemical diffusion coefficient for species i can be expressed as
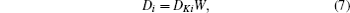
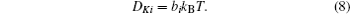
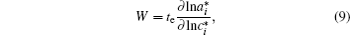
In addition to the widely studied factors mentioned above, some other factors also affect the Li-ion transport in electrode materials. Some important point defects, such as O vacancies, Li/ M ( M = transition metal ion) antisites, doping ions, and so on, are also strongly associated with Li mobility and conductivity. Luo et al . [ 90 ] showed that the oxygen vacancies in LiTi 2 (PO 4 ) 3 can substantially enhance rate capability. Koyama et al . [ 91 ] systematically study the defect chemistry in a series of layered LiMO 2 . Their results also emphasized the role of the defects in the electrochemical performance for the layered cathode materials. The Li/ M antisite defects and doping cations in LiMPO 4 olivine are typical defects that influence the Li diffusion and electronic conductivity. [ 92 ] Furthermore, the Li-ion transport is also sensitive to the external strain [ 93 ] and particle size [ 94 ] of the material; both of these relationships are demonstrated clearly in the LiFePO 4 cathode.
According to the band theory, we can evaluate the electronic conduction behavior simply by analyzing the electronic structure of the material. Materials with metallic electronic structures generally exhibit good electronic conductivity, and so are called conductors. Insulating electronic structure is associated with a band gap and low electronic conductivity. When the band gap is small, such materials are classified as semiconductors.
Quantitatively, two approaches have been developed and widely used to describe electronic conduction characteristics: classic electron transport theory and quantum transport theory. From the classical point of view, electrical conduction is considered to be a flow of free electron gas. When a flow of free electron gas reaches the equilibrium state under an external electric field force and the internal friction force, we can observe a constant current density in the material. With the relaxation time approximation, the electrical conductivity can be obtained from [ 95 ]

From the quantum mechanical concept, only those electrons located near the Fermi level contribute to electrical conductivity. Those states drift in k -space due to an external electrical field with a high velocity approximately equal to the Fermi velocity ( v F ), and only their movement in the direction of the electric field is considered. Thus, only these electrons participate in conduction, and conductivity can be described by [ 95 ]
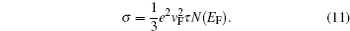
Another useful quantity to characterize electron conduction is electron mobility. The relationship between conductivity and mobility is expressed as [ 10 ]

The electron transport character of an electrode material is one important factor in evaluating its rate performance. During the charge/discharge process, electrons/charge must be transferred from (to) the electrode through an external circuit. Electron transport in the solid electrode can be described by electrical conductivity, which is a measurement of the electrode material’s ability to conduct electric current.
According to band theory, materials with a metallic electronic structure, that is, their Fermi level lies in their conduction band, have a large number of free conduction electrons available for electron transport. In these materials, electrical conductivity is very high. For LIB materials, the electronic structure of graphite anodes exhibits a metallic electronic structure, and the electron transport in a graphite anode is fast – its electrical conductivity is measured to be ∼10 4 s·cm −1 . [ 96 ] For most carbon anode materials, electrical conduction behavior is similar to that of graphite materials. [ 97 ] Technically, as carbon has good electrical conductivity, it can be used as a coating material to enhance the electrical conductivity of electrode materials with poor electrical conductivity. [ 98 – 102 ]
However, materials with insulating electronic structures (that is, the position of their Fermi level lies within their band gap) have poor electrical conduction ability, because the concentration of the free conduction electrons (charge carrier) in those materials is very low under room temperature. In those materials, free conduction charge carriers (electrons and holes) can be generated through thermal excitation of electrons from the fully occupied valence band to the fully empty conduction band, from which free holes and electrons are created in the valence and conduction band, respectively. The electrical conductivity of those materials continues to increase as the charge carrier density increases. In most of the oxide electrode materials, the electronic structure is insulating. The band gaps of the three typical cathode materials LiCoO 2 , LiMn 2 O 4 , and LiFePO 4 are presented in Table
| Table 2. Room-temperature conduction property of various cathode materials. . |
Thermally exciting electrons at room temperature to hop from the valence band to the conduction band is very difficult for most of the oxide electrodes, because the thermal energy k B T is only ∼ 23 meV at room temperature, while the band gaps are at least hundreds of meV or even several eV, as shown in Table
Although doping and other defects can enhance the electrical conductivity of oxide materials in many cases, they introduce other problems. For example, Cr doping in the Li site of the LiFePO 4 compound can solve the problem of electrical conductivity, [ 111 ] but it deteriorates Li diffusion, since the large Cr atom may block the one-dimensional Li diffusion pathway. [ 65 , 73 ] Furthermore, defects in the oxide materials also harm structural stability, and thus worsen cycling performance as electrode materials. It is known that the Ni/Li antisites in LiNiO 2 and LiNi x Co y Mn 1− x − y O 2 are at least partly responsible for the poor cycling performance of those layered cathodes. Xia et al. [ 116 ] reported that oxygen deficiency is harmful to the structural stability of the spinel cathode LiMn 2 O 4 , although O vacancies may favor electrical conduction.
In addition to the free electron conduction mechanism, small polaron conduction is quite important in the oxide materials with insulating electronic structures. In 1993, Goodenough et al . suggested that small polaron conduction is more of a concern in oxide cathodes. [ 117 ] Since then, few papers focused on this mechanism until more recently, with the development of first principles calculation techniques. Generally, the polaron concept was proposed to describe the electron-phonon interaction in dielectric crystals. The polaron state is formed and localizes or traps the electron and therefore lowers electron mobility. This trapping or localization effect gives rise to the insulating electronic structure in electrode materials. Taking the LiMn 2 O 4 compound as an example, when the localization effect is not considered, Mn atoms are in an average oxidation state of Mn 3.5+ and the electrons are “shared” by Mn atoms, which results in the metallic electronic structure. [ 118 ] However, Mn-3d orbital is able to localize (trap) the electrons and the oxidation state exhibits as half Mn 3+ and half Mn 4+ . The Mn 3+ holds one more electron than Mn 4+ , and the excess electron is localized at the Mn-3d- z 2 orbital, which lowers the energy of the crystal through the local lattice Jahn–Teller distortion. A localized electron at the Mn-3d- z 2 orbital combined with the local lattice distortion is called a Jahn–Teller type small polaron. [ 119 ] Figure
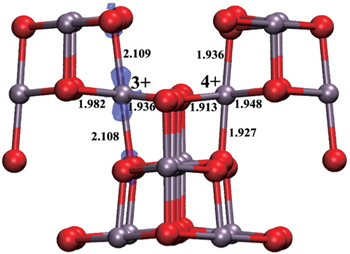 | Fig. 5. Polaron states in the λ -MnO 2 unit cell. Notations “+3” and “+4” around Mn atoms indicate their valence states. Mn–O bond lengths (in Å) are presented around each bond. The electron is localized at the 3d-state of the Mn 3+ atom, as shown by a transparent blue isosurface. The gray and red spheres are Mn and O atoms, respectively. [ 119 ] |
Although a polaron state localizes the electron and lowers the mobility of the conduction electron, the polaron state itself can be transported in the lattice, and can also transport charge and contribute to electrical conductivity. As the polaron state is associated with local lattice distortion, propagation of the lattice distortion in the crystal implies the transport of the localized electron. Studying the polaron conduction mechanism in LIB electrode materials helps us understand electrical conduction in those oxide compounds. Experimentally, as the polaron state is difficult to characterize, no report is available in the literature, as far as we know. On the other hand, computer simulation provides a powerful tool to study this problem. In 2006, Maxisch et al . [ 120 ] were first to study the formation and transport of small polarons in olivine Li x FePO 4 through DFT+U calculations. Their results show that excess charge can be localized at the Fe 2+ cations, thus forming small polarons, which can be transported among Fe 2+ and Fe 3+ cations with relatively low activation energy barriers. Later, Ouyang et al. studied the polaron state migration in the LiMn 2 O 4 compound and showed that polaron transport in LiMn 2 O 4 is important to its electrical conductivity. [ 119 ]
First principles calculations can be used to optimize the polaron migration pathway and calculate the polaron migration energy barrier, which is the most important parameter determining the mobility of the polaron state. However, electrical conductivity is also sensitive to the concentration and distribution of polaron states. In the LiMn 2 O 4 compound, the polaron state concentration decreases during the charging process because more Mn 3+ cations change into Mn 4+ upon Li removal. In the case of LiFePO 4 cathodes, the LiFePO 4 phase and FePO 4 phase are separated, and thus polaron migration occurs only at the phase boundary. Inside of the LiFePO 4 and FePO 4 phases, polaron migration is not very important because there is no polaron state available in the FePO 4 phase and no acceptor in the LiFePO 4 phase. When the polaron concentration is low, we can create those bound states through technical strategies. For example, Mn are all in the Mn 4+ oxidation state in the Li 2 MnO 3 cathode, and therefore no intrinsic polaron states exist in this compound. It has been shown that polaron states can be created in this compound through F-doping and replacing O atoms. [ 121 ] However, it has also been shown that those polaron states are trapped by the F atom in the lattice, and the mobility of the polaron states is low, which indicates that F-doping cannot help electrical conductivity much in the Li 2 MnO 3 cathode.
Charge transfer is a fundamental physical phenomenon in LIB electrode materials. In the present work, we briefly reviewed the elementary physical problems concerning the mechanisms of Li-ion diffusion and electron conduction, as described in the literature. Understanding the elementary physical transport problems of electrons and Li ions helps to design materials with better rate performance, which becomes more and more important with the growing demands from the EV industry. Demands for advanced LIBs emphasize not only high energy density but also high power density, which is directly determined by the charge and discharge speed and, in turn, by the rate performance of the battery.
Although many experiments and theories are developed to study the Li-ion diffusion problems in LIB materials, one very important problem is still unclear to the researchers: the Li migration energy barrier is high in some materials while it is low in other materials. More specifically, why is Li diffusion in some materials one-dimensional, while in some others it is two- or three-dimensional? In order to answer this question, we need to figure out more general rules, rather than empirical diffusion mechanisms, to explain the Li migration behaviors. For electron transport in electrodes, the question is less important for those materials with metallic electronic structures. Unfortunately, most cathode materials are insulators, due to their intrinsic electronic characteristics. Thermal excitation-generated free conduction charge carrier density is very low in those oxide cathodes. Doping can help enhance the electrical conductivity, but it also brings new problems. Polaron conduction can be an alternative to the free conduction electron transport in those materials. In order to improve a material’s electrical conduction performance, we can think of material design strategies that make use of polaron conduction, which is not often considered by most researchers. With further development of computational capacity and simulation techniques, computer simulation will help us with those designs.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 | |
| 102 | |
| 103 | |
| 104 | |
| 105 | |
| 106 | |
| 107 | |
| 108 | |
| 109 | |
| 110 | |
| 111 | |
| 112 | |
| 113 | |
| 114 | |
| 115 | |
| 116 | |
| 117 | |
| 118 | |
| 119 | |
| 120 | |
| 121 |