Hybrid inorganic–organic materials represent a new family in condensed matter physics. ^{[ 1 ]} The metal–organic frameworks (MOFs) consisting of networks of metal ions connected by coordinating organic linkers are good examples of such kind of hybrid materials. ^{[ 2 ]} Their great potential in applications such as catalytics, solar cells, and gas storage/separation has received intensive investigations in the last decade. ^{[ 3 – 5 ]} Meanwhile, the electric and magnetic properties of the hybrid MOFs are attracting more and more attention. ^{[ 6 – 10 ]} The MOFs can have diverse organic linkers (like CN, Cl, and C ₂ O ₄ ) and form different structures. In particular, the MOFs of ABX ₃ perovskite-like structure with formate linkers (O–CH–O) lie in the focus of this field because they show interesting magnetic properties and even multiferroics. For instance, the perovskite MOFs with a general formula of [(CH ₃ ) ₂ NH ₂ ] M (HCOO) ₃ ] ( M = Zn, Mn, Co, Fe, Ni) have been synthesized and studied. ^{[ 11 – 16 ]} Among them, the MOF with M = Fe ²⁺ (d ⁶ ) is of special interest because it exhibits very unusual magnetic behaviors as well as magnetoelectric multiferroicity at low temperatures.

The Fe-MOF has an ABX ₃ perovskite-like structure. The metal cations ( B = Fe ²⁺ ) bridged by the formate groups ( X = HCOO ⁻ ) form the BX ₃ frameworks, and the dimethylammonium (DM A ⁺ ) cations ( A = [(CH ₃ ) ₂ NH ₂ ] ⁺ ) occupy the cavities of the frameworks. In addition, the A groups are bonding to the formate linkers through the hydrogen bonds between the amine hydrogen atoms and the oxygen atoms of the formate bridges. Previous studies have revealed that the DM A ⁺ cations go through a dynamic disorder to a cooperative order upon cooling from the room temperature through 164 K due to the ordering of hydrogen bonding (N–H … O). ^{[ 13 ]} Furthermore, the hydrogen bonds have been proved to play an important role in the correlation between the B -site magnetic ions and the A -site organic cation. ^{[ 8 , 15 ]}

Recently, we have reported the observation of resonant quantum tunneling of magnetization in this Fe-MOF. ^{[ 17 ]} In this work, we focus on magnetic relaxation at low temperatures in the Fe-MOF. The results further demonstrate several features of resonant quantum relaxation, such as the exponential law with a single characteristic relaxation time, and the nonmonotonic dependence of the relaxation rate on the applied magnetic field, with enhanced relaxation around the resonant fields. The unusual magnetic behaviors of the Fe-MOF are discussed in terms of magnetic phase separation due to the modification of hydrogen bonding on the long-distance super-exchange interaction.

Single crystal samples of Fe-MOF were prepared by the hydrothermal method. A 30-mL N,N-Dimethylformamide (DMF) solution containing 5-mmol ferrous chloride salts and 30-mL deionized water was heated in a polyphenyl (PPL)-lined autoclaves for 3 days at 140 °C. ^{[ 12 ]} Then, cubic colorless crystals were obtained after slow evaporation for several days. The crystals were washed by ethanol several times, and then stored in a protective inert-gas atmosphere.

The x-ray diffraction (XRD) experiments of powder and single crystals were performed at room temperature using a Rigaku x-ray diffractometer. Powder XRD patterns have confirmed the structure and phase purity of the obtained samples. The single-crystal XRD pattern suggests that the crystal is naturally grown along [012] direction. All the magnetic properties were measured with a superconducting quantum interference device magnetometer (Quantum Design MPMS XL) on a single crystal along the [012] direction which is the magnetic easy axis.

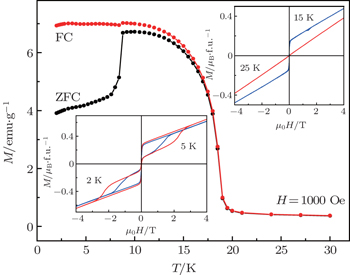
The magnetic transitions in the Fe-MOF are checked by measuring the temperature dependence of magnetization with an applied field of 1000 Oe after a zero-field-cooled (ZFC) or field-cooled (FC) process. As shown in Fig. 1 , there are two clear magnetic transitions between 2 K and 30 K. The first transition at T _N ∼ 19 K is evidenced by a rapid increase of magnetization. The M – H curves measured at temperatures above and below T _N are shown in the upper inset of Fig. 1 . At T = 25 K, the linear M – H curve indicates the paramagnetic state. At T = 15 K, it shows weak ferromagnetic feature in low magnetic fields and linear dependence in high magnetic fields. It is concluded that the transition at T _N ∼ 19 K is a paramagnetic to a spin-canted antiferromagnetic transition. The second transition is evidenced by a sharp decrease at ∼ 9 K in the ZFC curve. Below 9 K, the M – H curves show clear hysteresis. The large discrepancy between the ZFC and FC magnetization as well as the magnetic hysteresis below 9 K indicates that this transition is due to the blocking behavior of magnetic clusters or nanomagnets.

One unique feature of Fe-MOF is that it exhibits stair-shaped M – H hysteresis loops below T _B = 9 K. As shown in Fig. 2(a) , after subtracting the linear component in the M – H loops at 2 K and 5 K, we get very regular stair-shaped magnetization curves. Such kind of stair-shaped hysteresis loop at low temperatures is a strong characteristic of resonant quantum tunneling of magnetization, which has been generally observed in single-molecule and single-ion quantum magnets. ^{[ 18 – 24 ]} The differential of magnetization as a function of magnetic field is plotted in Fig. 2(b) . The sharp peaks correspond to the occurrence of resonant tunneling of magnetization in the Fe-MOF along [012]. Since it has a spin ground state of S = 2, the first resonant tunneling happens at H = 0 with a symmetrical double-well energy level scheme (+ 2 and −2, + 1 and −1), and the second one corresponds to the coincidence of + 2 and −1 (or −2 and + 1) levels at certain magnetic field. The first resonant tunneling field is around zero field, and the second resonant tunneling field decreases from 2.2 T to 1.5 T as the temperature increases from 2 K to 5 K.

Fig. 1.

	Figure Option View Download New Window
	Fig. 1. Magnetization along [012] as a function of temperature with both the ZFC and FC processes. Two magnetic transitions can be identified. The insets show the M – H isotherms at different temperatures.

Fig. 2.

	Figure Option View Download New Window
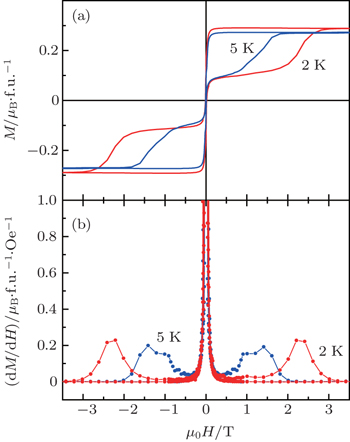	Fig. 2. (a) The stair-shaped M – H hysteresis loops at T = 2 K and 5 K, obtained after subtracting the linear component. (b) The differential of M – H curves at 2 K and 5 K.

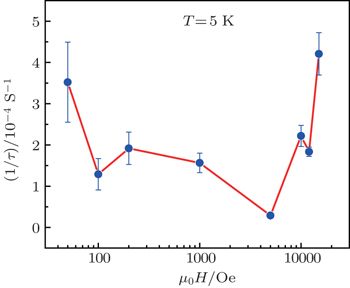
In order to further confirm the nature of quantum tunneling of magnetization in Fe-MOF, we have carried on a series of magnetic relaxation experiments at 5 K along the easy axis [012]. First, the sample was cooled from 40 K (at which it is in the paramagnetic state) to 5 K in zero field, then the magnetic field was applied and the magnetization was measured with time. The relaxation behavior at low magnetic fields and high magnetic fields are displayed in Figs. 3(a) and 3(b) , respectively. We try to fit the magnetization with an exponential relationship of time: M = M ₀ (1−e ^{−( t − t ₀ )/ τ} ), and the differences between the magnetization and the asymptotic value M ₀ as a function of time are displayed in a semi-logarithmic scale. After an initial fast relaxation for 1000 s–2000 s, these relaxation curves always show a linear dependence of time. Exponential relaxation is expected for an assembly of identical particles characterized by a single energy barrier, as discussed in the single-molecular nanomagnet [Mn ₁₂ O ₁₂ (CH ₃ COO) ₁₆ (H ₂ O) ₄ ](Mn12ac). ^{[ 18 ]} The observation of exponential relaxation of magnetization in Fe-MOF indicates the existence of identical nanomagnets with a single characteristic energy barrier instead of a collection of magnetic clusters with a broad size distribution.

Fig. 3.

	Figure Option View Download New Window
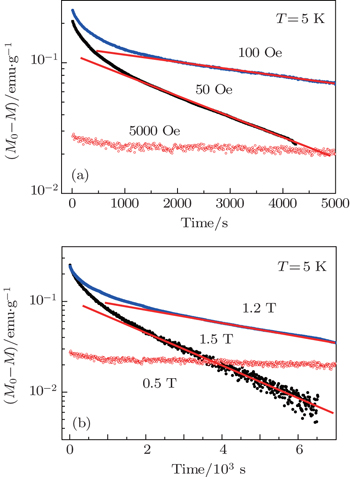	Fig. 3. Exponential magnetic relaxation at T = 5 K in (a) low magnetic fields and (b) high magnetic fields. The solid lines are the linear fits to the data.

As seen in Figs. 3(a) and 3(b) , the relaxation rate apparently depends on the applied magnetic fields. For instance, the relaxation in 50 Oe is faster than that in 100 Oe or 5000 Oe, and the relaxation rate of 1.5 T is larger than that of 1.2 T and 0.5 T. When the relaxation rates are plotted as a function of the applied magnetic fields, shown in Fig. 4 , the nonmonotonic field dependence is clearly seen: the magnetic relaxation is enhanced by the resonant tunneling and reaches the maximum around the resonant fields at 0 T and 1.5 T. This nonmonotonic behavior is consistent with the resonant tunneling of magnetization in the M – H loop around 0 T and 1.5 T at 5 K (Fig. 2 ). As 0.5 T is far away from the resonant fields, the relaxation in 0.5 T becomes very slow due to the larger tunneling energy barrier.

Both the stair-shaped hysteresis loop and the exponential relaxation with a nonmonotonic field dependence are characteristics of resonant quantum tunneling of magnetization.

Fig. 4.

	Figure Option View Download New Window
	Fig. 4. Nonmonotonic dependence of relaxation rate on applied magnetic fields at 5 K.

In the following, we try to understand the unusual magnetic behaviors of the Fe-MOF based on a long-distance super-exchange model. In transition-metal oxides, the transition-metal cations are separated by one oxygen atom and the magnetic ordering is due to super-exchange (Fig. 5(c) ). The strength of super-exchange strongly depends on the geometry of the exchange path and can be estimated by the Goodenough–Kanamori rules. ^{[ 25 ]} When the transition-metal cations M are separated by two ligand atoms, the exchange interaction through the M – L ₁ – L ₂ – M path is called super-super-exchange interaction. ^{[ 26 , 27 ]} Here, in the Fe-MOF, the transition metal cations (Fe ²⁺ ) are separated by a formate group (O–CH–O) so that the exchange interaction involves at least three ligand atoms (Fig. 5(b) ). We call this kind of super-exchange over multiple intermediate atoms a long-distance super-exchange (LDSE). The strength of the LDSE, like the conventional super-exchange, should be sensitive to the geometry of exchange path.

As illustrated in Fig. 5(a) , in order to stabilize in the perovskite structure the DMA cations in the A -site have to form hydrogen bonds through the N atom of the DMA cation and the O atom of the O–C–O linker. At high temperatures, the hydrogen bonds are dynamically disordered. Below the ferroelectric transition temperature, each N atom selects one of three equal positions. Because each DMA cation provides two hydrogen bonds, only 2/3 linkers contain hydrogen bonds. As a consequence, there are two types of linkers in the framework: one is the pure formate group and another is the formate group coupled with the DMA cation via a hydrogen bond. The exchange interaction through these two kinds of linkers could be very different. The Fe ²⁺ cations linked by a pure formate group allow the LDSE through the Fe–O–C–O–Fe exchange path, which leads to a spin-canted antiferromagnetic ordering. Otherwise, when a hydrogen bond is involved between the DMA group and the formate linker, the LDSE would be strongly depressed according to the Goodenough–Kanamori rules. The bond angle of the O–C–O exchange path and the overlap of the p orbitals of O and d orbitals of Fe ²⁺ would be decreased due to the attractive potential induced by the hydrogen bond. Thus the Fe ²⁺ with a relatively strong uniaxial magnetic anisotropy ^{[ 28 ]} would be isolated owing to the failure of LDSE interaction, when it is surrounded by hydrogen bond coupled linkers. Those isolated Fe ²⁺ ions without LDSE interaction would behave as single-ion quantum magnets. This picture can qualitatively account for the coexistence of both spin-canted antiferromagnetic order and single-ion quantum magnets in the Fe-MOF, and the magnetic phase separation is simply due to the distribution of hydrogen bonds in the framework.

Fig. 5.

	Figure Option View Download New Window
	Fig. 5. Schematic diagram of (a) the exchange path in the Fe-MOF; (b) the long-distance superexchange interaction; and (c) the conventional superexchange interaction.

The perovskite Fe-MOF exhibits very unusual magnetic behaviors at low temperatures, characterized by two magnetic transitions, and the resonant quantum tunneling of magnetization, as evidenced by the stair-shaped magnetization hysteresis loops and the nonmonotonic field dependence of exponential magnetic relaxation. The coexistence of two magnetic phases, i.e., canted antiferromagnetic ordering and single-ion quantum magnets, is interpreted by taking into account the action of hydrogen bonds on the long-distance super-exchange through a formate group linker. We propose that the hydrogen bonds can determine magnetic interaction by modifying the geometry of exchange path. This is very likely when the exchange path is long so that it is more sensitive to disturbances and distortions, such as in the hybrid metal–organic frameworks.