Recently, the lithium ion battery has been recognized as an alternative energy source for various portable electronics, due to its high gravimetric and volumetric capacity and the ability to deliver high rates of power. ^{[ 1 – 3 ]} However, current lithium battery technology cannot meet the requirements for ever increasing power in applications such as hybrid electric vehicles. This has aroused great interest in developing a new generation of Li-ion batteries with energy density larger than the current one. As is well known, the development of Liion batteries depends largely on the advancement of the new materials of battery electrodes with the high gravimetric and volumetric capacity of Lithium. Currently, graphite ^{[ 4 ]} is most commonly used as an anode for the Li-ion battery due to its high reversibility and stable capacity over repeated cycling. Nonetheless, a theoretical maximum capacity of the lithium ion is only about 372 mAh/g for normal graphite material, in which one Li atom can be intercalated for every six carbon atoms. Though it is found that the Li storage capacity can be increased up to 500–1000 mAh/g in grapheme, ^{[ 5 , 6 ]} carbon nanotubes, ^{[ 7 ]} and nanoribbons, ^{[ 8 ]} the limited capacity is still far from the desired requirements of current electric devices. Silicon has been proved to be a promising alternative to the graphite anode due to its high specific charge capacity of about 4200 mAh/g, which is about 10 times larger than that of graphite materials. ^{[ 9 ]} However, large volume expansion (larger than 300%) ^{[ 10 ]} upon lithium insertion has caused pulverization or mechanical fractures in micrometer particles and bulk silicon.

Nano-crystallization of silicon material has the potential to solve this limitation by managing the large stresses associated with the expansion and contraction of alloy anodes during electrochemical alloying. Especially, nanostructured material has additional advantages such as high rate capability due to the large volume ratio, short lithium diffusion distance, and lower diffusion energy barrier. Various nanoscale morphologies of silicon including thin films, ^{[ 11 – 14 ]} nanowires, ^{[ 15 , 16 ]} nanotubes, ^{[ 17 – 20 ]} and nanoparticals ^{[ 21 , 22 ]} have been investigated to minimize electrode pulverization and capacity loss in silicon anodes. For example, the Li-ion battery with Si nanowires as the anode can achieve specific energy capacity as high as 4200 mAh/g. ^{[ 15 ]} The most striking property of silicon nanowires as anodes is that they can sustain huge stresses to accommodate a large number of Li ions, which can avoid cracking the anodes after repeated charging and discharging cycles. Moreover, the energy barrier for Li atom diffusion toward the core of the silicon nanowires is in general lower than that for Li atom diffusion toward the surface. At the same time the Li atom has a strong tendency to stay inside the core of Si nanowires, which has been confirmed by the first principle calculations. ^{[ 23 ]} This situation would also lead to a faster charging of Li atoms into Si nanowires. Furthermore, Si nanowires possess excellent properties for Li atom insertion, such as efficient electronic translation along the axis and large Li ion flux due to the high surface-to-volume ratio. However, the diameters and growth directions of Si nanowires play important roles in the Li atom insertion and their diffusion energy barriers. It has been found that the diffusion barriers are significantly reduced with reducing the diameters of the Si nanowires. ^{[ 23 ]} Herein, one can expect excellent performance of the Li-ion battery with ultrathin silicon nanowires on account of great quantum confinement and the surface effect.

Slicene, a new two-dimensional (2D) silicon allotrope, has recently attracted tremendous attention due to its unique properties. ^{[ 24 , 25 ]} In experiment, silicene has been successfully fabricated by means of depositing silicon on Ag (111), Ir (111), and ZrB ₂ substrates. ^{[ 26 , 27 ]} Owing to the large surface and edges, silicene and its ribbon may possess more advantages as the anode material for the Li-ion battery. As a single layer structure like graphene, the removal of the Li atoms from the silicene surface is easy, and the insertion and extraction of Li atoms for the silicene can be enhanced. This will significantly reduce the first irreversible capacity, and improve the initial coulomb efficiency. Since the charging time and the power density of a battery are related to the ability for Li atoms to migrate efficiently through each of the electrodes and the electrolyte, it is extremely important to understand the diffusion of Li on silicene. In this work, we pay our attention to the diffusions of Li atoms in graphitic silicene and zigzag silicene ribbons. We find that the diffusion energy barrier in graphitic silicene is about 0.25 eV, lower than that in graphene (0.33 eV). Like diffusion on graphene ribbons, Li atoms have a strong tendency to stay at the edge of the silicene ribbons because those edge states are energetically more stable than others. And the energy barrier to diffuse toward the center of the silicene ribbons is in a range from 0.10 eV to 0.55 eV, in general lower than that to diffuse toward the center of silicon nanowires. The lower diffusion energy barrier may lead to a much faster charging/discharging of Li atoms onto/from the silicene ribbons than the case of the silicon nanowires.

All first principles calculations were performed by using the Vienna ab initio simulation program (VASP) ^{[ 28 ]} under the framework of density functional theory (DFT). We use a 42-atom supercell (4 × 4 unit cells) to simulate an infinite silicene sheet, and a 20-atom supercell with lattice constant 3.81 Å × 46.44 Å to simulate a zigzag nanoribbon. The Si atoms at the edge of the ribbon are passivated by H atoms to make sure that all the Si atoms have the coordinate number of four and no dangling bonds. The vacuum gap between the silicene and its images exceeds 15 Å, while the distance between one Li atom and its image is no less than 10 Å along the ribbon growth direction. Such a system is large enough to avoid any artificial interaction between images after careful testing. We used the projector augmented-plane wave (PAW) ^{[ 29 ]} method, and the exchange correlation was described self-consistently with a generalized gradient approximation (GGA) using the Perdew-BurkeErnzerhof (PBE) functional. A plane wave energy cutoff of 400 eV and a k -points mesh of 1 × 1 × 5 in the Monkhorst–Pack sampling scheme were used. The structural relaxation was performed using the conjugated gradient minimization method to make sure that the force on each atom is less than 0.02 eV/Å.

The silicene is firstly predicted through ab inito finite temperature molecular dynamics calculations within DFT by Cahangirov et al. ^{[ 30 ]} Unlike planar graphene, silicene is of a low-buckled honeycomb structure with lattice constant 3.82 Å. The buckling distance is about 0.47 Å while the buckling angle is about 12.03 degree. Four types of high symmetry adsorption sites are used to investigate the adsorption properties of Li atoms, which are denoted as T _L , T _H , B, and H, corresponding to the top of lower silicon, higher silicon, the center of the bridge and the hexagonal hollow site, as shown in Fig. 1 , respectively. The most favorable site is Li at the H site with a binding energy of –0.65 eV. Here, the binding energy is defined as

Fig. 1.

	Figure Option View Download New Window
	Fig. 1. The side view (a) and top view (b) of the atomic configuration for 3 × 3 supercell of silicene. α and Δ are the buckling angle and buckling distance, respectively. The high symmetry adsorption sites are denoted as T L , T H , B, and H, corresponding to the top of lower silicon, higher silicon, bridge site, and hexagonal hollow site, respectively.

Fig. 2.

	Figure Option View Download New Window
	Fig. 2. Diffusion path (a) and energy barrier (b) for Li on silicene sheet.

For a zigzag silicene nanoribbon, the dimensionality of silicene is reduced and the symmetry of the honeybomb lattice is broken, the center of the nanoribbon toward the edge is not equivalent any more. The diffusion path on the silicene nanoribbon along the growth axis can now be identified as A ₁ –A ₅ as shown in Fig. 3 . However, these paths are now nonequivalent and different from those in silicene sheet due to the broken symmetry. The number of nonequivalent paths depends on the ribbon width. In our case, we identify five nonequivalent paths along the ribbon axis. For nanoribbons with wider widths, similar results are obtained. From Fig. 3 , one can find that the diffusion channel is quite similar to that in silicene, that is, the path is –H–T _L –H– along the axis of silicene sheet. However, the diffusion energy barrier is quite different. Although the energy barrier for the diffusion channel in the center is almost the same as that in silicene, the energy barrier for the edge diffusion channel is reduced to 0.1 eV. However, the energy barrier is quickly convergent to the same value as that in silicene as shown in Fig. 4 . It seems that the edges have a weaker effect on the Li diffusion in silicene nanoribbons than in silicon nanowires. More importantly, the binding energy for Li adatoms in the edge range is much lower than that in the center. Obviously, the Li adatoms have a strong tendency to keep stable at the edge of the nanoribbon.

Fig. 3.

	Figure Option View Download New Window
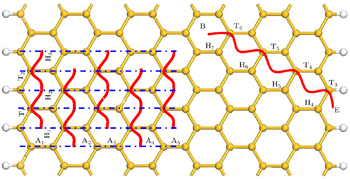	Fig. 3. Possible diffusion paths (A 1 –A 5 ) for Li adatoms on silicene nanoribbon along the ribbon growth axis and the path from the ribbon edge to center.

Fig. 4.

	Figure Option View Download New Window
	Fig. 4. (a) Energy barriers for A 1 –A 5 as shown in Fig. 3 . (b) Energy barrier versus diffusion path.

In order to identify the possibility of Li adatom entering the nanoribbons in charging and discharging processes, the diffusion paths and their barriers are shown in Figs. 3 and 5 . Li adatoms would follow a complex zigzag channel or a direct channel to migrate from the edge to the center of a nanoribbon as shown in Fig. 3 . Owing to the symmetry of zigzag nanoribbon, the energy barrier for a complex zigzag channel is the same as that for a direct channel. Here, we only give the energy barrier for the direct channel as shown in Fig. 5 . Firstly, the Li adatom should overcome an energy barrier of about 0.1 eV to enter into the first hexagon of the silicene nanoribbon, and then an energy barrier of about 0.5 eV to enter the next hexagon, the next following energy barrier ranging from 0.25 eV to 0.35 eV to enter the center of the nanoribbon. Although the energy barrier of 0.5 eV is much more difficult to overcome, it is much easier than for a Li adatom to diffuse from the outside into a Si nanowire (the energy barrier is about 0.85 eV). It means that the charging and discharging processes for a Li-ion battery with silicene ribbons as anodes are much easier than that with Si nanowires. Our results indicate that silicene nanoribbon may become an excellent anode material for the Li-ion battery.

Fig. 5.

	Figure Option View Download New Window
	Fig. 5. Energy barriers for Li migrating from the edge of the nanoribbon to the center along the path as shown in Fig. 3 .

In this work, we systematically study the diffusion of Li adatoms on silicene sheet and zigzag nanoribbons under the DFT framework. The results show that the Li adatoms follow an H–T _L –H diffusion channel with an energy barrier of 0.25 eV on silicene sheet. For silicene nanoribbon, the diffusion channel along the ribbon axis is the same as that on silicence sheet, but the energy barriers range from 0.1 eV to 0.25 eV for the channels from the edge to the center due to the edge effect. By comparing with the binding energy, we find that the Li adatom has a tendency to stay at the edge of the silicene nanoribbon. The largest diffusion energy barrier for a Li adatom entering the center of a nanoribbon from the edge is about 0.5 eV, which is much lower than that in Si nanowires. Our results show that the silicene nanoribbon promises to be an excellent anode material for the Li-ion battery.