† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11274039), the National Basic Research Program of China (Grant No. 2013CB922002), and the Fundamental Research Funds for the Central Universities of China.
We study the formation of vortices in a dipolar Bose–Einstein condensate in a synthetic magnetic field by numerically solving the Gross–Pitaevskii equation. The formation process depends on the dipole strength, the rotating frequency, the potential geometry, and the orientation of the dipoles. We make an extensive comparison with vortices created by a rotating trap, especially focusing on the issues of the critical rotating frequency and the vortex number as a function of the rotating frequency. We observe that a higher rotating frequency is needed to generate a large number of vortices and the anisotropic interaction manifests itself as a perceptible difference in the vortex formation. Furthermore, a large dipole strength or aspect ratio also can increase the number of vortices effectively. In particular, we discuss the validity of the Feynman rule.
Since the recent experimental realization of Bose–Einstein condensations (BECs) of 52 Cr, [ 1 ] 164 Dy, [ 2 ] and 168 Er, [ 3 ] which have magnetic dipole moments of 6 μ B , 7 μ B , and 10 μ B , respectively, much effort has been devoted to understanding the physics of dipolar BECs. [ 4 , 5 ] The two most important characteristics of the dipole–dipole interaction (DDI) are its long range and anisotropic nature, which give rise to a few striking experimental signatures, such as rich spin textures, [ 6 , 7 ] modified low-lying excitations, [ 8 ] and strong dipolar nature of a quantum ferrofluid. [ 9 ]
One important issue in connection to the BECs is that the vortex formation and structure exhibit various novel physical phenomena under the influence of the dipolar interaction, together with other interactions and geometries. The vortices with different symmetries such as triangular, square, stripe-like, and bubble-like were theoretically explored. [ 10 – 12 ] The ground state of a rotating BECs displays a rich variety of vortex patterns, such as flower-like lattice, crescent, and snakeskin piebald. [ 13 – 15 ] In Ref. [ 16 ], the d-wave symmetric collapse and explosion of the condensate were experimentally observed, and the formation of vortex rings with opposite circulations was theoretically predicted.
All the aforementioned studies pertain to systems in which the vortices are created in a rotating frame of reference. It is similar to the rotating-bucket method of conventional low-temperature physics, [ 17 – 19 ] where a vortex is obtained by rotating a bucket full of water. Recently, Lin et al . [ 20 , 21 ] performed an experimental study of a synthetic magnetic field. As soon as the synthetic field exceeds a critical one, vortices enter the condensate and the number of vortices increases as the synthetic magnetic field strength increases. The author suggested that this method has advantages in comparison to a rotating frame, the latter is difficult to add optical lattices and large angular momenta, and the rotation is limited by heating and metastability.
Motivated by the pioneering experiment, we are interested in the formation of vortices in a synthetic magnetic field. This issue has been discussed in a BEC with only contact interaction. [ 22 ] In this paper, we investigate how the vortices behave under a synthetic magnetic field if DDI is added. For this goal, we consider a two-dimensional (2D) system that is confined in the xy plane with relatively large trap frequency ω z . We make an extensive comparison of the vortices generated by the two methods. Numerical results indicate that anisotropic superfluidity manifests itself as the directional dependence of the vortex formation. For the rotating frame, a key observation is that the system undergoes a transition from triangular lattice to stripe pattern when the rotating frequency approaches the upper limit. For the synthetic magnetic field case, the vortex row number and the vortex number are much smaller than those calculated for the rotating frame.
This paper is organized as follows. In Section 2, we outline the Gross–Pitaevskii (GP) equation for a dipolar BEC under a synthetic magnetic field in a 2D system. Details about how the numerical method is used are given. In Section 3, we study the properties of the system with various parameters, including the dipole strength, the rotating frequency, the aspect ratio of the trap, and the orientation of the dipole moment of the atoms. It is shown that the behaviors of the system in the synthetic magnetic field are quite different compared to those in the rotating frame. Section 4 gives a brief conclusion.
Consider a system of bosonic neutral atoms of mass m . In the weak interaction limit, the dipolar condensate in a synthetic magnetic field can be described by the non-local GP equation
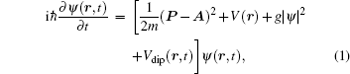
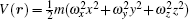
The mean-field dipolar interaction term V dip (
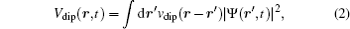
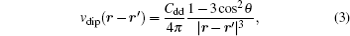

Before proceeding further, we transform the GP equation into a dimensionless form, where the spatial coordinates are normalized by the characteristic harmonic oscillator length 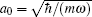
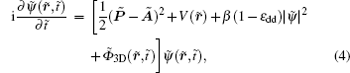
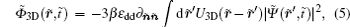
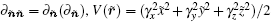

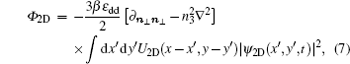
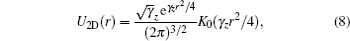
For comparison, the corresponding 2D dimensionless GP equation for BECs in a rotating frame is provided
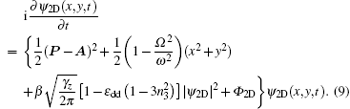
In the numerics, we use the norm-preserving imaginary time propagation method to solve Eqs. (
To analyze the influence of DDI on the formation of a vortex, we numerically solve the time-dependent GP equation. Our main purpose is to investigate phenomena characteristic of the vortex formation in a dipolar BEC induced by a synthetic magnetic field. In what follows we discuss this issue by regulating the strength of the dipolar interaction, the rotating frequency, the aspect ratio of the trap, and the orientation of the dipole moment of the atoms with respect to their plane of motion. We would like to highlight the difference between the two models. Throughout this paper, we will use Ω c1 / ω and Ω c / ω to denote the frequencies to generate a single vortex and certain number vortices, respectively.
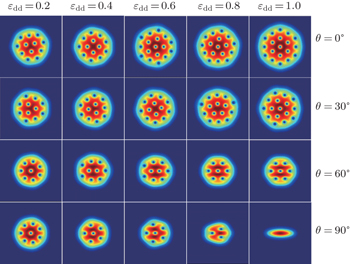
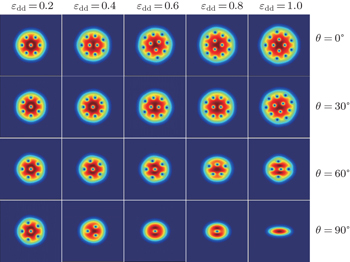
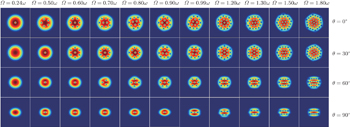
We first study the formation of vortices in the system as a function of the orientation of the dipoles of the atoms with respect to their plane of motion and of the dipole strength. In Figs.
From Figs.
When the polarization angle becomes θ = 30°, we find a similar behavior, the number of vortices increases and Ω c1 / ω decreases with increasing ε dd , as in this case, the repulsive part of the dipole interaction still dominates the condensate.
For θ = 60°, however, the dipolar interaction is mostly attractive. As a result, the number of vortices decreases and Ω c1 / ω increases with the increase of ε dd in the considered range. It is different from that observed in Ref. [ 25 ], where the vortex number is independence of ε dd .
When the angle becomes θ = 90°, the behavior of the system changes. In this case, the attractive part of the dipole interaction becomes dominant, preventing the formation of vortices. Thus the number of vortices decreases and Ω c1 / ω increases with increasing ε dd . We also observe that the vortex number in the synthetic magnetic field is less than that in the rotating frame for the same dipole strength.
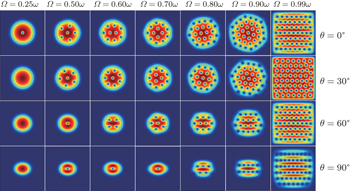
We also study the formation of vortices as a function of the rotating frequency Ω and the dipole orientation θ for fixed β = 100 and ε dd = 0.8. Figures
For the BEC confined in the rotating trap, the vortex number increases rapidly with increasing Ω . When the dipoles are polarized in-plane along the z axis ( θ = 0°), the expansion of the density reported in the previous subsection due to the purely repulsive nature of the dipolar interaction accelerates the formation of vortices, especially when Ω approaches the trapping frequency ω . For example, there are 37 vortices at Ω = 0.90 ω and the vortex number increases to 57 at Ω = 0.99 ω , which is just the upper limit of the rotating frequency. In the meantime, the system undergoes a transition from triangular lattice to stripe pattern. The stripe vortex lattices in the present study are not observed in Ref. [ 11 ].
The same qualitative behavior is found when the polarization angle θ is increased. Indeed, for θ = 30°, the main difference from the previous case is that the number presents a slight reduction.
The triangular lattice is, however, no longer observed for θ = 60°, regardless of the value of the rotating frequency. In this case, the stripe pattern occurs at earlier Ω = 0.80 ω .
When the dipoles are polarized along the horizontal direction, i.e., when θ = 90°, the dipolar interaction is repulsive along the y axis and attractive along the x axis, as a consequence, the number of vortices decreases compared to that with θ = 60° for the same rotating frequency.
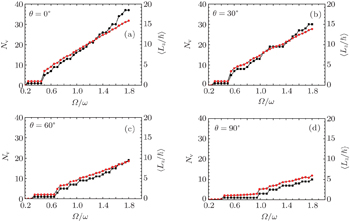
In the synthetic magnetic field case, it is obvious that the vortex number grows much more slowly. Four cases are considered, namely, θ = 0°, 30°, 60°, 90°. In the case of Ω = 0.99 ω , the corresponding numbers of vortices are 16, 13, 7, and 3, respectively. When the rotating frequency is increased to Ω = 1.80 ω , the number of vortices increases, and the corresponding values become 37, 30, 19, and 10, respectively. In this large Ω case, no stripe pattern is obsevered for both θ = 0° and 30° cases and the vortex row number is reduced to 4 and 2 for the θ = 60° and 90° cases.
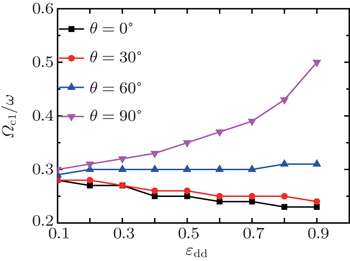
The above results show that it is hard for vortices to be created by the synthetic magnetic field. In order to elaborate this point further, we plot the dependence of the equilibrium vortex number N v on critical rotating frequency Ω c / ω in Fig.
The explanation of these differences lies in the confinement of the trapping potential, Eq. (
As a natural extension, we also examine the Feynman rule in the synthetic magnetic field, which has been studied in the rotating frame. [ 26 , 27 ] The Feynman rule gives a relation that links the total number of vortices N v with the rotating frequency Ω . For a superfluid rotating in a rigid container with radius R , by assuming a spatially homogeneous density, the number of vortices can be determined as [ 28 ]
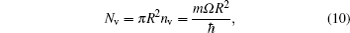
Figure
The most important results obtained in this section are summarized as follows. (i) The synthetic magnetic field can make the system remain stable at higher rotating frequency ( Ω > ω ). (ii) The number of vortices and the vortex row number are smaller in the synthetic magnetic field than those in the rotating frame at the same Ω . (iii) The synthetic magnetic is low efficient. In the next section, the effect of the aspect ratio will be discussed.
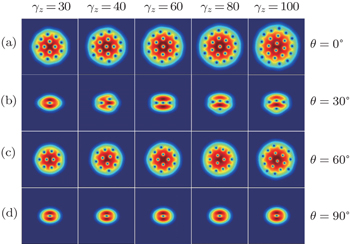
In this section, we briefly discuss the effect of the trap aspect ratio, γ z = ω z / ω , on the formation of vortices. This issue has been discussed for 3-dimensional (3D) condensates in the rotating frame and it is indicated that increasing γ z helps nucleation of the vortex. [ 29 ] Although the 3D system is converted into an effective 2D model in the present study, the trap aspect ratio γ z can be quantitatively considered since it is included in equivalent contact interaction 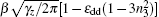
 | Fig. 8. The critical rotating frequency Ω c1 / ω as a function of the aspect ratio γ z and the orientation of dipoles θ in synthetic magnetic field. The constants are taken as ε dd = 0.8 and β = 100. |
In Figs.
We investigate the formation of vortices in a dipolar BEC in a synthetic magnetic field. In contrast to the rotating frame case where the system is unstable when the rotating frequency Ω is larger than the radial trap oscillator frequency ω , the strong confinement in the synthetic magnetic field can lead the system to remain stable at higher rotating frequency ( Ω > ω ). We find that the number of vortices generated by the synthetic magnetic field is much smaller than that by the rotating frame under the same condition, which reveals that the synthetic magnetic field is less efficient in creating vortices. We also confirm that strengthening the dipole strength or increasing the trap aspect ratio can create more vortices. Finally, the validity of the Feynman rule is checked.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 |