Cite this Article
Xu Ning, Li Jian-Fu, Huang Bo-Long, Wang Bao-Lin. A new family of sp 3 -hybridized carbon phases. Chinese Physics B , 2016, 25(1): 016103  
Permissions
A new family of sp 3 -hybridized carbon phases
Xu Ning 1, †, , Li Jian-Fu 2 , Huang Bo-Long 2 , Wang Bao-Lin 1
Department of Physics, Yancheng Institute of Technology, Yancheng 224051, China
Department of Physics and Materials Science, City University of Hong Kong, Hong Kong, China

 

† Corresponding author. E-mail: nxu@ycit.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11174242, 11204265, 11404278, 11147007, and 11274151), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK2012248), and the Scientific Research Foundation of Yancheng Institute of Technology, China (Grant No. KJC2014024).

Abstract
Abstract

A new family of superhard carbon allotropes C48(2 i + 1) is constructed by alternating even 4 and 8 membered rings. These new carbon allotropes are of a spatially antisymmetrical structure, compared with the symmetrical structures of bct -C4, Z -carbon, and P -carbon. Our calculations show that bulk moduli of C48(2 i + 1) are larger than that of c -BN and smaller than that of cubic-diamond. C48(2 i + 1) are transparent superhard materials possessing large Vicker hardness comparable to diamond. This work can help us understand the structural phase transformations of cold-compression graphite and carbon nanotubes.

PACS : 61.66.Bi ; 61.50.Ks ; 62.50.–p ; 78.30.Am
Keyword : low-temperature phase transformation ; superhard carbon phase
1. Introduction

Superhard materials play an important role in fundamental science and technological applications, and thus they have been widely used in numerous industrial fields, such as cutting, drilling tools, polishing, and coatings for surface protecting. [ 1 , 2 ] Among them, diamond is the hardest known material because of the nature of their strong sp 3 -hybridized covalent bonding, and has been used to fulfill most of the above mentioned industrial needs. Most of the natural diamonds are formed by carbon-containing minerals under the conditions of high temperature and pressure in the Earth’s mantle. Therefore, amorphous carbon, graphite, fullerene, and carbon nanotubes (CNTs) are considered as the potential precursors to synthesize diamond-like materials in high pressure experiment. For example, graphite can be converted into the hexagonal (or cubic) diamond at pressures above 15 GPa and high temperature (1600–2500 K). [ 3 ] In contrast, cold compression of graphite, [ 4 – 14 ] single-walled and multi-walled CNTs [ 15 – 21 ] result in superhard carbon allotropes, which exhibit superior mechanical performance with the ability to indent single-crystal diamond [ 9 , 15 ] and differ from the crystal structure of hexagonal and cubic diamond. Consequently, several hypothetical structures are proposed to shed light on the superhard mechanism. [ 22 – 30 ] The experimental crystal structures of cold-compressed phases of CNTs and graphite are currently still under debate. Therefore, it is essential to examine its intrinsic structure to understand the unexpectedly high indentation hardness of the cold-compressed phases of CNTs and graphite.

When we pay more attention to the previously proposed allotropes, the bct -C4 phase and Z -carbon interest is due to its unique structure. [ 25 – 28 ] Interestingly, all of them can be constructed through sliding and buckling of the graphene sheets. Meanwhile, the bct -C4 phase can be observed at the interface of Z -carbon. The crystal structure of bct -C4 is shown in Fig.  1(a) , indicating the simplest 4+8 rings pattern along the armchair orientation (direct face-to-face opposed connection of two armchair chains). Similarly, a new carbon allotrope C48 is constructed as shown in Fig.  1(b) . The new C48 allotrope is different from bct -C4, although it has 4+8 rings. Considering all possible even rings of carbon (4+8 membered rings in C48, six-membered rings in hexagonal diamond), many additional possible combinations (shown in Figs.  2(a) and 2(b) ) could be expected. Therefore, it is very interesting to seek a general scheme to understand the principles of the structural formation of possible alternative superhard allotropes related to cold-compressed CNTs and graphite.

Fig. 1. (a), (b) Crystallo-graphic structures of the bct -C4 and the proposed C48 carbon, and (c) 2×2×1 supercell structure of C48 phase.
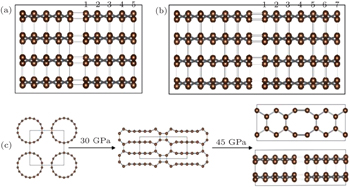Fig. 2. (a), (b) 2D projections of the 2×2×1 suppercell of C48(5) and C48(7), and (c) high-pressure phase transition of (9,0) CNTs under different compressions.

In the present work, we report on a new family of sp 3 -hybridized carbon allotropes by discussing the topological stacking of carbon atomic chains consisting of even 4 and 8 membered ring patterns. From Fig.  2 , we find that the C48(2 i + 1) carbon allotropes can be constructed by connecting malposed hexagonal to hexagonal diamond along the z axis. These new phases are labelled by C48(2 i + 1) ( i = 1, 2, …). 2 i + 1 respresents the number of layers of atoms. The conventional unit cell for C48(2 i + 1) carbon has 4 i atoms. The structures of these new phases differ from those of M -carbon, Z -carbon, W -carbon, P -carbon, S -carbon, R -carbon, and X -carbon. [ 31 ] In Fig.  2(c) , we show a possible transition pathway from (9, 0) carbon nanotube to C48(5). We find that (9, 0) CNT retains its tubular structure in a pressure range from 0 to 30 GPa. The pressure-induced structure transition takes place at a pressure of 32 GPa, in which (9, 0) CNT collapse. When pressure is above 45 GPa, C48(5) can be obtained.

2. Method of calculation

The calculations were carried out by using density functional theory as implemented in the Vienna ab initio simulaiton package (VASP) [ 32 ] with the projector augmented-wave method employed to describe the interaction between the nucleus and valence electrons. The general gradient approximation (GGA) of the Perdew Burke Ernzerhof (PBE) parameterization [ 33 ] was adopted to describe the exchange and correlation function. A plane-wave basis set with a cutoff energy of 700 eV was used and Monkhorst–Pack [ 34 ] k meshes were chosen to ensure that all the enthalpy calculations are well converged to better than 1 meV/atom. Forces on the ions were calculated through the Hellmann–Feynman theorem allowing a full geometry optimization.

Regarding the new structural models we explored, the precisions of the electronic structures we forecast are mainly determined by both the accuracy of the lattice optimization and the corresponding Thomas–Fermi screening length averaging scheme that is for sX-LDA calculations. In the CASTEP code, the Thomas–Fermi screening length ( k TF ) of sX-LDA was determined by evaluating the dynamical average charge density within our newly predicted structures. [ 35 ] We took this feature to accomplish the prediction of the electronic structures of the newly determined structures. This is currently unavailable in VASP but we still rely on VASP-predicted geometry structures due to their perfect balance between efficiency and accuracy. Phonon calculations have been carried out by using a supercell approach as implemented in the PHONOPY code. The XRD patterns for various structures were performed by the Materials Studio package.

3. Results and discussion

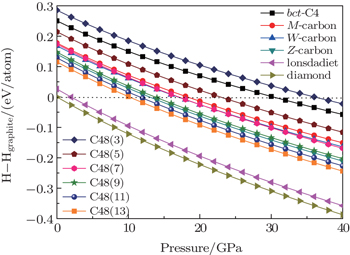
In order to investigate the relative stabilities of C48(2 i + 1) phases, the calculated enthalpy difference at zero temperature with respect to graphite for different allotropes are compared in Fig.  3 as a function of pressure. It is shown that the C48(2 i + 1) structures with i > 4 are more stable than the bct -C4, M -carbon, W -carbon, and Z -carbon. Only bct -C4 has (almost) the largest enthalpy. C48(3) is the less stable structure than the others, and C48(5) is only more stable than bct -C4. The enthalpy value per atom of the C48(2 i + 1) phase tends to be the value of hexagonal diamond with the increase of i .

Fig. 3. Plots of calculated enthalpy difference per atom with respect to graphite versus pressure for a series of carbon allotropes. Graphite is denoted with the horizontal line at zero. The stable pressures of these proposed allotropes compared with that of graphite are labeled.

Based on the sX-LDA method, the electronic band structure is calculated at zero pressure. E g = 5.476 eV and E g = 6.11 eV are obtained respectively for cubic and hexagonal diamond, which match well with the experimental results. [ 36 ] It is shown that the C48(3) carbon is a wide gap insulator with energy gap E g = 5.647 eV, which is higher than that of cubic diamond and samller than that of hexagonal diamond. Analyses of electron localization functions (ELFs) (see Fig.  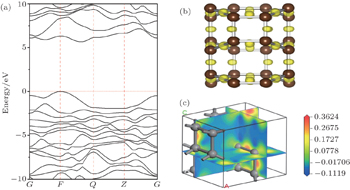4(b) ) and charge density difference (see Fig.  4(c) ) suggest that C48(3) carbon is sp 3 -hydriddized. The electron density between atoms increases with increasing pressure. These results show that the C48(3) carbon is a transparent material. Smilar properties are observed in the other C48(2 i + 1) carbon phases as shown in Table  1 . The C48(5) carbon has the smallest band gap E g = 4.743. The band gap for C48(2 i + 1) phases increases with i and tends to be the value of hexagonal diamond E g = 6.11 eV.

Fig. 4. (a) Calculated electronic band structure at zero pressure; (b) calculated ELF isosurface at ELF = 0.9; and (c) charge density difference for C48(3).
Table 1.

Space group, lattice parameters (LP), densities ( D : g·cm −3 ), band gaps ( E g : eV), bulk moduli ( B 0 : GPa), shear moduli ( G : GPa), Young’s moduli ( Y : GPa), Poisson’s ratios ( ν ), and Vicker’s hardness for bct -C4, M -Carbon, W -Carbon, Z -Carbon, Lonsdadiet, diamond, and C48.

.

The mechanical properties, such as bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, and Vicker’s hardness for bct -C4, M -carbon, W -carbon, Z -carbon, hexagonal diamond, cubic diamond, C48(2 i + 1) are summarized in Table  1 . It is shown that the calculated lattice parameters, density, bulk modulus, and shear modulus for cubic diamond match well with the experimental results. [ 3 , 36 ] Further studies show that the density of C48(2 i + 1) carbon phases is sparser than that of cubic and hexagonal diamond, and increases with i value increasing. The similar changing trends are observed in bulk modulus, shear modulus and Young’s modulus. In contrast, Poisson’s ratio decreases with the i value increasing. There are many empirical formula to simulate the Vicker’s hardness. [ 37 , 38 ] In the present work, Vicker’s hardness for these carbon alltropoes are calculated according to the method proposed by Gao et al. [ 37 ] We find that the C48(2 i + 1) carbon phase possesses a large Vicker hardness comparable to diamond.

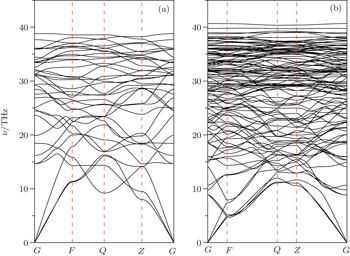
The stability of a structure cannot be determined exclusively by comparing enthalpy since the structure might be subject to dynamic instabilities. Therefore, phonon dispersion curves for C48(2 i + 1) are further calculated by the supercell method. In the present work, we focus on C48(3) and C48(5). C48(3) and C48(5) can be constructed by connecting malposed hexagonal to hexagonal diamond along the z axis and a grain boundary between the hexagonal diamond is observed. The primitive cell of the C48(3) phase contains 12 atoms, giving 36 phonon branches. Around the Γ point, three phonon dispersion curves are observed and no imaginary phonon frequencies are found in the whole brillouin zone (see Fig.  5(a) ), indicating that the C48(3) is dynamically stable at zero pressure. Similar properties are observed in the C48(5) phase and the other C48(2 i + 1) phases as shown in Fig.  5(b) . The 60 phonon branches are found in Fig.  5(b) , owing to 20 atoms in a unit cell of C48(5).

Fig. 5. Calculated phonon dispersion curves at 0 GPa for (a) C48(3) and (b) C48(5).

Finally, the XRD patterns of bct -C4, M -carbon, W -carbon, Z -carbon, hexagonal and cubic diamond, C48(2 i + 1) phases have been simulated for instructing the experiment, by using 0.3329 Å radiation. [ 39 ] At zero pressure, the simulated intensive peak positions and relative intensities of cubic and hexagonal diamond match the experimental results very well. As is well known, each phase has its own characteristic peaks, which correspond to different crystal planes. The XRD patterns for C48(2 i + 1) phases are shown in Fig.  6 . Thus the nano-polycrystalline structures of C48(2 i + 1) phases, constructed from carbon nanotube and graphite, can be further identified according to the additional characteristic peaks. The XRD patterns present important theoretical guidance for the experiment and can help us understand the structural phase transition of high-pressure CNTs and graphite.

Fig. 6. Simulated XRD patterns of bct -C4, M -carbon, W -carbon, Z -carbon, hexagonal diamond, cubic diamond, and C48(2 i + 1) phases (0.3329 Å radiation).
4. Conclusions

In this work, we perform a comprehensive study on the lowest-enthalpy carbon phases and the phase transformation mechanisms for cold-compressed CNTs and graphite. Our calculations reveal that the phase transformation initiates and proceeds along the pathways with lowest enthalpy toward a new family of sp 3 -hybridized C48(2 i + 1) phases. The cold-compressed carbon phases, constructed from CNTs and graphite, may consist of C48(2 i + 1) and previously proposed bct -C4, M -carbon, W -carbon, Z -carbon, P -carbon, S -carbon, R -carbon, and X -carbon. It would be reasonable to expect that the cold-compressed phase of CNTs and graphite can be interpreted as a mixture of several of the proposed allotropes. The present results provide an excellent account for the experiment on the cold-compressed CNTs and graphite, they also provide an insight into the understanding of high-temperature phase transformation pathways for carbon structures.

Reference
1 Kaner R B Gilman J J Tolbert S H 2005 Science 308 1268
2 Li K Y Wang X T Zhang F F Xue D F 2008 Phy. Rev. Lett. 100 235504
3 Irifune T Kurio A Sakamoto S Inoue T Sumiya H 2003 Nature 421 599
4 Utsumi W Yagi T 1991 Science 252 1542
5 Hanfland M Syassen K Sonnenschein R 1989 Phys. Rev. B 40 1951
6 Yagi T Utsumi W Yamakata M A Kikegawa T Shimomura O 1992 Phys. Rev. B 46 6031
7 Takano K J Harashima H Wakatsuki M 1991 Jpn. J. Appl. Phys. 30 L860
8 Zhao Y X Spain I L 1989 Phys. Rev. B 40 993
9 Mao W L Mao H K Eng P J Trainor T P Newville M Kao C C Heinz D L Shu J Meng Y Hemley R J 2003 Science 302 425
10 Hanfland M Beister H Syassen K 1989 Phys. Rev. B 39 12598
11 Goncharov A F Makarenko I N Stishov S M 1989 Sov. Phys. JETP 69 380
12 Bundy F P 1967 J. Chem. Phys. 46 3437
13 Utsumi W Yagi T 1991 Science 252 1542
14 Xu N Li J F Huang B L Wang B L Wang X L 2015 Materials Research Express 2 045601
15 Wang Z W Zhao Y S Tait K Liao X Z Schiferl D Zha C S Downs R T Qian J Zhu Y T Shen T D 2004 Proc. Natl. Acad. Sci. 101 13699
16 Tang J Qin L C Sasaki T Yudasaka M Matsushita A Iijima S 2000 Phys. Rev. Lett. 85 1887
17 Khabashesku V N Gu Z N Brinson B Zimmerman J L Margrave J L 2002 J. Phys. Chem. B 106 11155
18 Popov M Kyotani M Nemanich R J Koga Y 2002 Phys. Rev. B 65 033408
19 Popov M Kyotani M Koga Y 2003 Diam. Relat. Mater. 12 833
20 Bucknum M J Castro E A 2006 J. Chem. Theory Comput. 2 775
21 Kumar R S Pravica M G Cornelius A L Nicol M F Hu M Y Chow P C 2007 Diam. Relat. Mater. 16 1250
22 Li Q Ma Y M Oganov A R Wang H B Wang H Xu Y Cui T Mao H K Zou G T 2009 Phys. Rev. Lett. 102 175506
23 Oganov A R Glass C W 2006 J. Chem. Phys. 124 244704
24 Selli D Baburin I A Martonnak R Leoni S 2011 Phys. Rev. B 84 161411
25 Amsler M Flores-Livas J A Lehtovaara L Balima F Ghasemi S A Machon D Pailhès S Willand A Caliste D Botti S San Miguel A Goedecker S Marques M A 2012 Phys. Rev. Lett. 108 065501
26 Zhao Z S Xu B Zhou X F Wang L M Wen B He J L Liu Z Y Wang H T Tian Y J 2011 Phys. Rev. Lett. 107 215502
27 Wang J T Chen C F Kawazoe Y 2011 Phys. Rev. Lett. 106 075501
28 Umemoto K Wentzcovitch R M Saito S Miyake T 2010 Phys. Rev. Lett. 104 125504
29 Niu H Y Chen X Q Wang S B Li D Z Mao W L Li Y Y 2012 Phys. Rev. Lett. 108 135501
30 Zhou R L Zeng X C 2012 J. Am. Chem. Soc. 134 7530
31 Xu N Li J F Huang B L Wang B L Wang X L 2015 Mater. Res. Express 2 045601
32 Kresse G Fürthmuller J 1996 Phys. Rev. B 54 11169
33 Blochl P E 1994 Phys. Rev. B 50 17953
34 Monkhorst H J Pack J D 1976 Phys. Rev. B 13 5188
35 Clark S J Segall M D Pickard C J Hasnip P J Probert M I J Refson K Payne M C 2005 Z. Kristallogr 220 567
36 Occelli F Loubeyre P Letoullec R 2003 Nat. Mater. 2 151
37 Gao F He J Wu E Liu S Yu D Li D Zhang S Tian Y 2003 Phys. Rev. Lett. 91 015502
38 Chen X Q Niu H Y Li D Z Li Y Y 2011 Intermetallics 19 1275
39 Xu N Li J F Huang B L Wang B L Wang X L 2015 Mater. Res. Express 2 045601