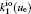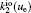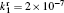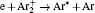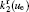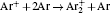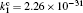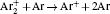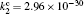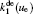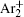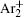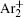
Argon is an interesting inert gas for numerous applications in different areas of science and technology: for surface sputtering and plasma processing, ^{[ 1 ]} it is used in a mixture for filling light bulbs and fluorescent tubes, ^{[ 2 ]} and it is used in gas filled switches for pulsed power technology, ^{[ 3 ]} as a working gas for plasma jets, ^{[ 4 ]} dielectric barrier discharges, ^{[ 5 ]} welding and thermal processing, ^{[ 6 ]} etc. The relaxation kinetics in argon was studied by a microwave and optical technique following microwave discharge in order to determine the electron–ion recombination coefficient and its electron temperature dependence. ^{[ 7 – 9 ]} By applying the microwave technique in conjunction with a quadrupole mass spectrometer, the time evolutions of electron and ion number densities were determined to take place about ten milliseconds after the afterglow. ^{[ 10 – 12 ]} Recently, by applying pulsed voltages with different repetition frequencies and rise times, the different breakdown characteristics were established, depending on residual charged and neutral active particles. ^{[ 13 ]}

During the study of gas-filled surge arresters by Bošan, ^{[ 14 – 16 ]} it was established that the mean value of the electrical breakdown time delay t̄ _d depends on the relaxation time (afterglow period) τ from the cessation of the previous discharge to the next application of the working voltage U _w to the gas tube. The t̄ _d ( τ ) dependence (“memory curve”) has been used for tracing the active particle decay in afterglow of AC and DC discharges in inert and molecular gases and was explained by the action of metastable states remaining from the preceding glow. ^{[ 14 – 16 ]} Recently, the metastable hypothesis was repeated by specifying Ar ( ³ P ₀ ) and Ar ( ³ P ₂ ) metastable states as the explanation of the memory curve in argon. ^{[ 17 , 18 ]}

Elementary considerations show that metastable states are efficiently quenched by collisions between ground-state atoms and molecules of parent gases, as well as by collision with impurities and collision between themselves, their effective lifetimes in afterglow are reduced down to the order of milli- and microseconds and cannot explain the long-term memory. ^{[ 19 – 21 ]} Consequently, a new model was proposed to explain the memory effect in nitrogen based on the surface recombination of nitrogen atoms ^{[ 21 – 23 ]} and in hydrogen by surface recombination of hydrogen atoms. ^{[ 23 – 25 ]} The memory curve in argon was measured from very short relaxation times in afterglow up to the saturation region (determined by cosmic rays and natural radioactivity level) and was explained by the charged particle decay and after that, by surface recombination of nitrogen atoms present as impurities. ^{[ 26 ]} This was recently confirmed by introducing a controlled quantity of nitrogen impurities into argon in a pulsed radio frequency atmospheric pressure glow discharge. ^{[ 27 ]}

The relaxation behavior in argon is considered in a gas tube with plane parallel electrode geometry, by using a 1D numerical model of the stationary DC glow discharge for calculating the charged particle number densities, and the approximate analytical and 2D numerical model of the afterglow relaxation. The rest of this paper is organized as follows. The short description of the experiment is given in Section 2, by describing the experimental procedure and gas tube preparation. In Section 3, the description of the analytical model is used to determine the dominant process and corresponding coefficients, a 1D numerical model is used to calculate the number densities of dominant particles during the stationary state of DC glow discharge, and a 2D numerical model for afterglow relaxation is presented. Finally, in Section 4, the short conclusion is given.

The time delay measurements are carried out in a gas tube filled with argon. The tube is made of borosilicate glass 8245 (Schott technical glass). The electrodes are made of oxygen free high conductivity (OFHC) copper, each with diameters D = 2.2 cm with mildly rounded edges to avoid the edge effect. In comparison with the arrangement in Ref. [ 26 ], the plane parallel electrodes with much greater diameter have a good particle collection efficiency, enabling the measurements of formative time delay distributions. The electrodes are tightly fitted into the tube in order to prevent the long-path breakdown (Fig. 1 ).

Fig. 1.

	Figure Option View Download New Window
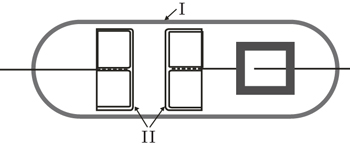	Fig. 1. Schematic diagram of gas discharge tube for the present measurements, made of borosilicate glass (I) with plane parallel copper electrodes (II).

In the tube, the inter-electrode distance can be changed by using a magnet outside. The gas tube was pumped down to a pressure of 10 ⁻⁵ Pa, degassed at 650 K and then filled with argon at a pressure of 200 Pa with less than 1 ppm of impurities.

The time delay measurements were carried out at inter-electrode distances d = 1, 1.5, and 2 cm with corresponding breakdown voltages U _s = 210, 230, and 250 V, respectively. The memory curves were measured at different working voltages and inter-electrode distances. The relaxation time was varied from 1 ms to the saturation region of the memory curve determined by cosmic rays and natural radioactivity, while the glow time was constant t _g = 1 s, long enough to reach stationary conditions. The time delay measurements were carried out with 100 data in the series and the tube was protected from the external light during the measurements. More details about the experimental procedure and tube preparation can be found in Refs. [ 21 ]–[ 26 ].

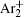
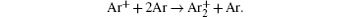
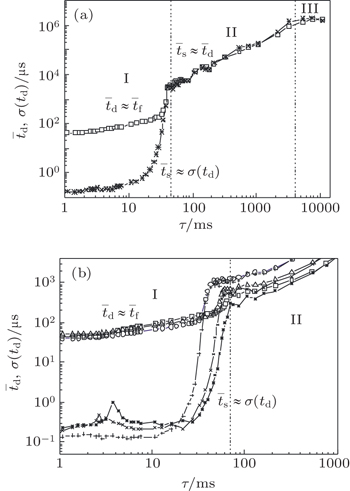
The charged particle decay during the relaxation of the DC discharge in argon at low pressure is governed by atomic Ar ⁺ and molecular ions, produced by Ar ⁺ ion conversion in a three-body association process ^{[ 28 ]}

The memory curves measured at different inter-electrode distances (volumes) are shown in Fig. 2 . In Fig. 2(a) , which shows the memory curve measured from 1 ms to 10 s, the three characteristic regions can be observed. ^{[ 30 ]}

Fig. 2.

Figure Option View Download New Window

Fig. 2. Memory curves with different regions measured at pressure p = 200 Pa, glow current I g = 130 μA: (a) at working voltage U w = 250 V and inter-electrode distance d = 1 cm, and (b) at 50% overvoltage, i.e., U w = 315 V, 345 V, and 375 V and d = 1, 1.5, and 2 cm ( t̄ d : mean value of electrical breakdown time delay, t̄ f : formative time delay, t̄ s : statistical time delay, σ ( t d ): standard deviation of time delay, and τ : relaxation time).

Region I is dominated by charged particle decay, region II by the neutral active particle decay (surface recombination of nitrogen atoms present as impurities), ^{[ 26 , 27 ]} and finally, region III by the saturation of memory curve (due to cosmic rays and natural radioactivity). ^{[ 26 , 27 , 30 ]} By analyzing the memory curves measured at different inter-electrode distances the same regions can be observed. The significant differences are the occurrences of maxima of mean values and standard deviations of time delay at the relaxation time of about several milliseconds (Fig. 2(b) ). We assume that these maxima occur due to the change of dominant initiating particles, i.e., the conversion of an atomic into molecular argon ion. Further, by analyzing the time delay distributions at these relaxation times we will try to confirm this assumption.

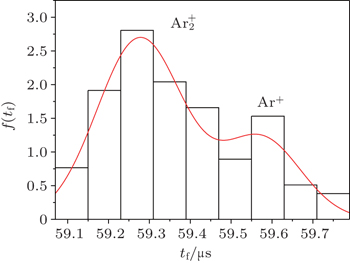
The double-Gaussian distribution of breakdown time delay (Fig. 3 ) is observed at working voltage U _w = 250 V, glow current I _g = 130 μA, inter-electrode distance d = 1 cm, and relaxation time τ = 5 ms, in the region where the conversions of maxima occur in memory curves (Fig. 2(b) ). In this region, the statistical time is negligible ( t̄ _s ≈ 1/ Y _eff ≈ 1/( YP ) → 0, where Y is the electron yield and P is the breakdown probability), ^{[ 22 , 29 , 30 ]} so the measured time delay distributions are in fact the formative time delay distributions ( t̄ _f ≈ t̄ _d ≫ t̄ _s ).

Fig. 3.

	Figure Option View Download New Window
	Fig. 3. Double-Gaussian distributions of the formative time delay measured at working voltage U w = 250 V, glow current I g = 130 μA and inter-electrode distance d = 1 cm at relaxation time τ = 5 ms, indicating the existence of two particle types involved in the formation process (the bars are experimental data and the line is an analytical fit of Eq. ( 1 )).

This distribution (Fig. 3 ) is fitted with the double-Gaussian distribution function ^{[ 31 ]}

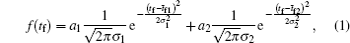
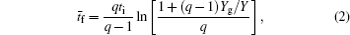
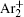
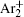
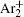
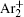
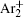
The statistical time delay of breakdown becomes greater with the increase of relaxation time and at about 20 ms the statistical time delay becomes dominant. By analyzing the memory curve from Fig. 2(a) , the exponential rise of statistical time delay at the relaxation times above 25 ms can be seen. The experimental confirmation is obtained by transforming this part of the memory curve into a semi-logarithmic plot, where the linearization of statistical time delay as a function of relaxation time can be observed (Fig. 4 ).

Fig. 4.

	Figure Option View Download New Window
	Fig. 4. Linearization of the statistical time delay of breakdown in a semi-logarithmic plot as a function of relaxation time at working voltage U w = 250 V, glow current at I g = 130 μA, inter-electrode distance d = 1 cm, and pressure p = 200 Pa (symbols are experimental data and the line is the analytical fit of Eq. ( 4 )).

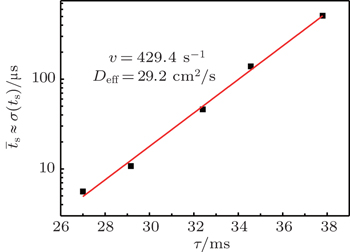
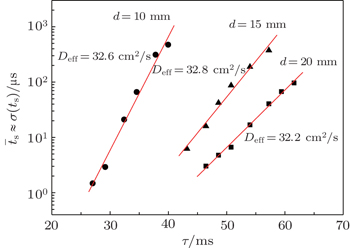
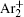
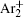
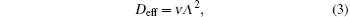
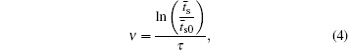
According to the approximate analytical model, ^{[ 35 ]} the exponential rise of statistical time delay implies the exponential fall of the number density of the dominant ion. At the low pressure, the diffusion of ionic species to the tube walls is the most dominant loss. In the previous analysis, we assume the conversion of Ar ⁺ into at about 2.5 ms, hence the dominant ions at this relaxation time should be ions. From the slope of linear fit, the diffusion coefficient is determined by using the following relation:

Fig. 5.

	Figure Option View Download New Window
	Fig. 5. Linearizations of statistical time delay of breakdown in a semi-logarithmic plot as a function of relaxation time at working voltages U w = 315, 345, and 375 V at inter-electrode distances d = 1, 1.5, and 2 cm, glow current I g = 130 μA, and pressure p = 200 Pa, respectively (symbols are experimental data and lines are analytical fits of Eq. ( 4 )).

From the slopes of linear fit of experimental data, approximately the same value of diffusion coefficient is determined from Eqs. ( 3 ) and ( 4 ), as in the previous case (taking into account that Λ ² = 0.068 cm ² for d = 1 cm, Λ ² = 0.109 cm ² for d = 1.5 cm, and Λ ² = 0.138 cm ² for d = 2 cm), which indicates the presence of the same dominant ions in the range between 20 and 60 ms. In the following, we will try to support our previous assumptions by using the numerical models.

3.1. Numerical models for stationary state and relaxation of glow discharge in argon

In order to confirm the previous assumptions, to determine the dominant processes and particles and to discuss their influences on the relaxation, the numerical models for the stationary glow discharge and the relaxation are used. For the modeling of relaxation, the initial number densities must be calculated first, so we use the fluid model with nonlocal ionization. ^{[ 36 , 37 ]} In the following, we will give a brief description of these models and discuss the obtained results.

3.1.1. One-dimensional (1D) fluid model for stationary number density calculation

The stationary number density profiles are required in order to use them as initial particle number densities in a relaxation model. The most common numerical models which are used for the modeling of different types of gas discharge are fluid models. ^{[ 36 – 39 ]} The nonlocal fluid model for argon discharge presented in Ref. [ 36 ] is used to calculate stationary profiles in DC discharge in argon under working conditions. The results from this model show that they are in very good agreement with the experimental data. ^{[ 36 , 37 ]} The main idea of the fluid model with nonlocal ionization is to incorporate the ionization by fast electrons into the fluid model. The fluid model consists of the continuity equation for particle number density and the energy balance equation. In addition, Poisson’s equation is coupled with these equations. Hence, the complete system of equations for a fluid model with nonlocal ionization is as follows:

where n _j are the number densities of particles, Γ _j are their corresponding fluxes, S _j are source terms which contain all the production and loss processes of particles (index j in previous relations represents the type of particle, i.e., electron, ions, and metastables), φ is the electric potential, e is the elementary charge, ɛ ₀ is the vacuum permittivity, u _e is the mean electron energy, Γ _u is the electron energy flux, and S _u is the electron energy source term for energy gain and loss in reactions. Fluxes of electrons, ions, metastable states of atoms, and electron energy flux have the following forms:

where μ _e and μ _i are the electron and ion mobilities, while D _e , D _i , and D _m are the diffusion coefficients of particles, i.e., electron, ions, and metastables, respectively.

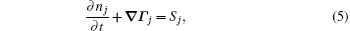
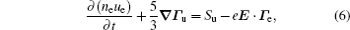
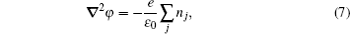
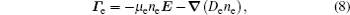
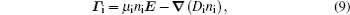
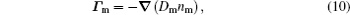
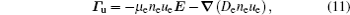
The source term for fast electrons has the following form: ^{[ 36 ]}

where Γ _e (0) is the electron flux on the cathode, α is the Townsend’s ionization coefficient, d _c is the cathode sheath region where the electric field is strong, z is the distance from the cathode surface, and λ is the characteristic scale of decay. ^{[ 36 , 40 ]} The value of Townsend’s ionization coefficient is obtained by fitting the experimental data. ^{[ 37 , 41 ]}

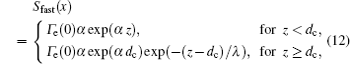
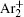
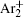
In order to determine the most dominant particles in the argon DC discharge and relaxation, the following analysis is conducted. Since the work function of copper is ϕ _i = 4.42 eV, ^{[ 42 ]} electrons are mostly emitted from the surface due to the potential emission by ions, i.e., Ar ⁺ and ions. Therefore, these ions are inevitably included in the model. In addition, metastable states of argon can have an influence on the stationary state and also on relaxation of DC discharge. Argon atoms have two metastable states, ³ P ₂ and ³ P ₀ , respectively, with energy levels of 11.55 eV and 11.72 eV, which are very close to each other. Hence, in our model Ar* represents both metastable states. In addition, an argon atom has two closely resonant levels ³ P ₁ and ¹ P ₁ with energy levels 11.62 eV and 11.83 eV, respectively. These resonant levels are not considered in the model because of their fast radiation decays. ^{[ 43 ]} Therefore, according to the previous analysis, in our model for the stationary state of argon DC discharge we include 4 dominant particles, i.e., electron, Ar ⁺ , , and Ar*. Processes for these particles are given in Table 1 .

Table 1.

Table 1.

Table 1. Reactions included in 1D fluid model and 2D model for relaxation. . No. Reactions Rate coefficients/cm 3 ·s −1 , cm 6 ·s −1 Reference 1 e + Ar → Ar + + e + e [44] 2 e + Ar* → Ar + + e + e [44] 3 e + Ar + → Ar [45] 4 Ar* + Ar* → Ar + Ar + + e k Pe = 6.3 × 10 −10 [19] 5 [46] 6 [28] 7 [46] 8 e + Ar → Ar* + e k ex ( u e ) [44] 9 e + Ar* → Ar + e [44] 10 e + Ar* → Ar r+e k dr = 2 × 10 −7 [47] a 11 Ar* + 2Ar → Ar 2 + Ar k de2 = 1.1 × 10 −32 [19] 12 Ar* + Ar → 2Ar k de1 = 3 × 10 −15 [47] a Ar r is resonant state of argon atom.

Table 1. Reactions included in 1D fluid model and 2D model for relaxation. .

The complete form of particle source terms for stationary state of discharge is

where E ^ion = 15.76 eV is the ionization energy of an argon atom, and E ^ex = 11.635 eV is the mean value of excitation energies of ³ P ₂ and ³ P ₀ argon metastable states.

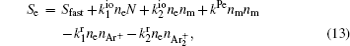
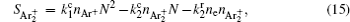
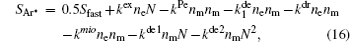
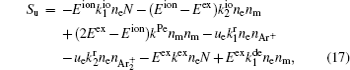
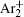
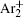
For modeling the stationary state of glow discharge, the values of mobility and diffusion coefficient for the electron each are taken as a function of the mean energy. ^{[ 44 ]} The mobility for Ar ⁺ depends on the reduced electric field, ^{[ 48 ]} while the mobility for has an approximately equal value for the large range of reduced field. ^{[ 33 ]} For Ar ⁺ and ions, the diffusion coefficients are cited from Refs. [ 11 ] and [ 12 ] and for the metastable state from Ref. [ 19 ].

The equation for the external circuit given by Ohm’s law is also included and used to calculate the voltage on the discharge tube from

where I _g is the glow current, R is the resistance, U _w is the working voltage applied to the tube, and U _g is the voltage between electrodes. The glow current is calculated by multiplying the sum of charge particle fluxes with electron charge and cathode surface area. At the initial time t = 0, the glow voltage and working voltage are equal U _g = U _w , and afterwards U _g is calculated from Ohm’s law. The number densities of the charged particles are taken to be zero at the electrodes, while the flux of electrons leaving the cathode is

where γ is the secondary electron yield calculated from the breakdown condition for given pd value.

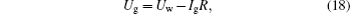
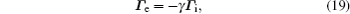
This system of Eqs. ( 5 )–( 7 ) cannot be solved analytically, therefore numerical methods have to be used. First, the system is discretized by the implicit finite difference method, ^{[ 49 ]} while the fluxes Eqs. ( 8 ), ( 9 ), and ( 11 ) are expanded by the Sharfetter–Gummel scheme. ^{[ 50 ]} In this way, the system of linear equations is obtained which is further solved by using the Thomas algorithm. ^{[ 51 ]} The calculations are carried out with 120 spatial steps and with a time step Δ t = 10 ⁻¹⁰ s.

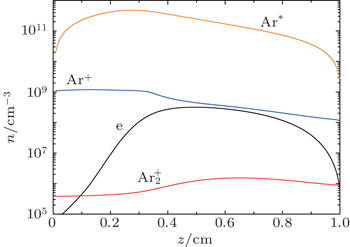
The number density profiles in the stationary state of DC discharge at working voltage U _w = 250 V and current I _g = 130 μA at the pressure p = 200 Pa and inter-electrode distance d = 1 cm calculated from the fluid model with non local ionization are given in Fig. 6 .

Fig. 6.

	Figure Option View Download New Window
	Fig. 6. Number density profiles in the stationary state of DC discharge, obtained by the fluid model with non local ionization at working voltage U w = 250 V, glow current I g = 130 μA at pressure p = 200 Pa, and inter-electrode distance d = 1 cm.

From Fig. 6 , it can be seen that Ar ⁺ ions have the highest number density due to the dominant electron impact ionization, while the number density is slightly lower. The calculated number densities are in a good agreement with the experimental results measured by the Langmuire probe under similar conditions. ^{[ 52 ]} These number densities are further substituted as initial densities into the 2D model for relaxation.

3.1.2. Two-dimensional model for relaxation

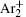
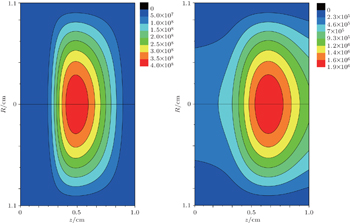
The two-dimensional model for relaxation of DC discharge ^{[ 53 ]} is used to model the relaxation of argon discharge at low pressure. This model consists of a diffusion equation for dominant particles with the source term, which includes all dominant processes of productions and losses of corresponding particles, and is described as follows:

where n _j are the particle number densities, D _j are the diffusion coefficients, and S _j are the source terms (index j represents the type of particle, i.e., electron, ion, and metastable state). Since the tube is of a cylindrical shape (Fig. 1 ), it is more appropriate to solve the problem in cylindrical coordinates as

The number density profiles calculated with the 1D non local fluid model ^{[ 37 ]} are taken as initial densities for the relaxation, where the calculated profiles are taken as the number densities on axis, while the radial profile is taken to be the Bessel profile

where J ₀ is a zeroth-order Bessel function of the first kind. The initial 2D number density profiles of electrons and ions are given in Fig. 7 .

Fig. 7.

	Figure Option View Download New Window
	Fig. 7. Initial 2D number density profiles of (a) electrons and (b) ions, taken as initial number densities for the relaxation, where the axial profile is calculated by the 1D fluid model with non local ionization, while the radial profile is a Bessel one.

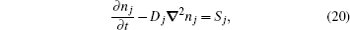
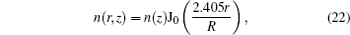
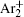
The system of partial differential equation ( 21 ) cannot be solved analytically, hence the numerical method is used. The implicit finite difference method is used to discretize the differential equations, from which the system of linear equations is obtained. This system of equations is further solved by the successive over-relaxation (SOR) method. ^{[ 51 ]}

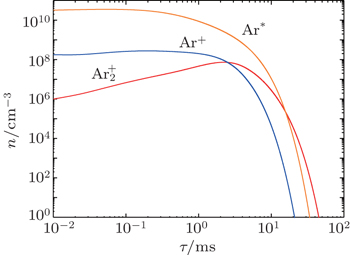
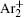
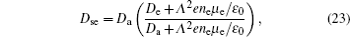
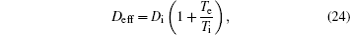
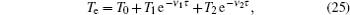
As mentioned previously, the dominant particles that could lead to the secondary electron emission and affect the initiation of breakdown are Ar ⁺ , , Ar*, and Ar, hence they are included in the model for relaxation. The corresponding reactions are listed in Table 1 (except ionization and excitation). The dominant loss process in DC discharge relaxation at low pressure is the diffusion of charged particles to the walls. In order to describe the relaxation correctly in the model, the change of diffusion regimes must be taken into account. In the beginning of the afterglow the space charge still exists in inter-electrode space, hence the ambipolar regime is still present. When the electron and ion number densities fall, the regime changes into non-isothermal diffusion and the effective electron diffusion is described by the following expression: ^{[ 54 ]}

where D _a = ( μ _i / μ _e ) D _e is the ambipolar diffusion coefficient, n _e is the electron number density, Λ is the characteristic diffusion length of the tube, μ _e is the electron mobility, μ _i is the ion mobility, ɛ ₀ is the vacuum permittivity, and e is the elementary charge. In this case, the following relation for effective ionic diffusion is used: ^{[ 55 ]}

where D _eff is the effective diffusion coefficient, D _i is the free diffusion coefficient of ions, T _e is the electron temperature, and T _i is the ion temperature (equal to gas temperature T _g ). The expression for the ionic diffusion Eq. ( 24 ) depends on the electron temperature. Therefore, the analytical fit of electron temperature decay measured in relaxation needs to be used ^{[ 11 , 12 ]} as follows:

where T ₀ is the room temperature, and T ₁ , T ₂ , ν ₁ , and ν ₂ are the fitting parameters. When the electron temperature falls to room temperature, the diffusion regime is isothermal and the effective diffusion coefficient is D _eff = 2 D _i . Finally, the diffusion goes into the free diffusion regime at around 45 ms when D _eff = D _i . The transition from isothermal to free diffusion is described by the linear dependence D _eff ∼ Λ / λ _D . ^{[ 23 , 35 ]}

Besides the diffusion loss, the conversion plays an important role in the relaxation. Namely, the choice of conversion coefficient in the numerical model ((0.69 − 4.7) × 10 ⁻³¹ cm ³ /s at the room temperature ^{[ 11 , 28 ]} ) plays an important role in modeling the relaxation. For instance, the choice of the smallest value of the conversion coefficient that can be found in the literature (0.69 × 10 ⁻³¹ cm ³ /s) leads to the conversion maximum at approximately 6 ms. Opposed to that choice of conversion the coefficient 4.7 × 10 ⁻³¹ cm ³ /s shifts the conversion maximum to approximately 1.5 ms. With the conversion coefficient 2.26 × 10 ⁻³¹ cm ³ /s the time of change of dominant particle (Fig. 8 ) is closest to the experimental one (Fig. 2(b) ). The evolutions of the average number densities of ions and metastable states in front of the cathode surface calculated from the model, are given in Fig. 8 .

Fig. 8.

	Figure Option View Download New Window
	Fig. 8. Number density profiles of dominant particles in relaxation of DC discharge in front of the cathode surface at working voltage U w = 250 V, glow current I g = 130 μA, pressure p = 200 Pa, and inter-electrode distance d = 1 cm.

It can be seen that the Ar ⁺ number density falls quite rapidly after several milliseconds due to diffusion and conversion, while the ion number density remains at a longer relaxation time. The number densities of Ar ⁺ and are approximately equal at about 2.5 ms when the change of dominant initiating particle takes place. After that, the number density of ions in the inter-electrode gap is higher than that of Ar ⁺ ions. In this way, the previous assumption that the double-Gaussian distribution is caused by and Ar ⁺ ions, is supported. Besides , the metastable states Ar* also have an influence on the early relaxation. Namely, the metastable states affect Ar ⁺ number density by metastable–metastable ionization, which maintains their number density in the longer relaxation time and shifting the conversion maximum rightwards.

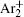
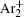
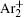
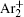
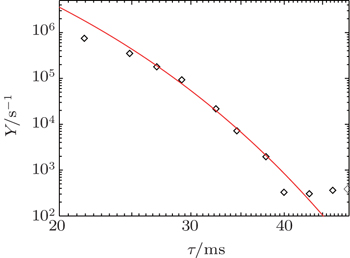
Finally, the effective electron yield, i.e., the number of electrons generated in the inter-electrode space per second, ^{[ 22 ]} is calculated from the numerical model and used to fit the experimental data (Fig. 9 ), and the yield is expressed as

where γ is the secondary electron yield, S is the front cathode surface area, Γ is the flux of particles leading to the secondary emission of the initiating electrons, n _i is the number density of dominant ions, w _i is the drift velocity of dominant ion, and C is the probability that one electron produced at the cathode is able to survive and initiate the breakdown. The number density is calculated from the model as an average value of the number density in the first axial step in the front of the cathode surface. From Fig. 8 , it can be seen that in the range between 20 and 60 ms the only particles with significant number density are ions, therefore only they can lead to the secondary electron emission. By using the following values of effective secondary electron yield determined from the breakdown condition γ _s = 0.02, drift velocity at working voltage w _i = 2.3 × 10 ⁵ cm/s, the front area of the cathode surface S = 3.8 cm ² , and linear dependence of effective diffusion coefficient D _eff ∼ Λ / λ _D , the satisfactory agreement with the experimental data is obtained (Fig. 9 ).

Fig. 9.

	Figure Option View Download New Window
	Fig. 9. Electron yield in relaxation of DC discharge in a time range from 20 ms to 45 ms, in which range the diffusion of is dominant loss, at working voltage U w = 250 V, glow current I g = 130 μA, pressure p = 200 Pa, and inter-electrode distance d = 1 cm (symbols are experimental data, and the solid line is given by the numerical model).

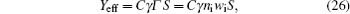
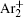
The dominant process in the relaxation of DC glow discharge between plane parallel electrodes in argon at a pressure of 200 Pa are analyzed by measuring the breakdown time delay. The memory curves measured at different inter-electrode distances (volumes) are analyzed and the existence of three main regions is confirmed. In this study, we focus on the early relaxation period and charged particle decay with simultaneous conversion of Ar ⁺ to ions, and on the measurements of formative time delay distributions in this time interval. By analyzing the distribution of the formative time delay, the double-Gaussian distribution is observed, confirming the existence of two dominant particles. By comparing the mean values of the formative time delay of the two subpopulations, it is concluded that the dominant ions in this time interval are Ar ⁺ and ions. It is assumed that the Ar ⁺ ion is dominant at the relaxation times below 2.5 ms and after that, due to atomic-to- molecular conversion, ion becomes dominant at greater relaxation times. According to these assumptions, the exponential rise of statistical time delay in a range from 20 to 60 ms during the relaxation is governed by diffusion loss of ions to the walls. By using the approximate analytical model, the effective diffusion coefficient of the ion is estimated.

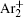
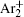
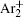
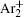
Further in the analysis, the numerical models are used in order to confirm the assumptions. First, the number densities of dominant particles in the stationary state of glow discharge at working conditions are calculated by applying the 1D fluid model, improving the estimations from the earlier paper. ^{[ 26 ]} Corresponding number densities are used as the initial ones for the relaxation modeling. The evolutions of number densities are calculated from the 2D numerical model. By varying the conversion coefficients found in the literature (the minimal, medium and high value), a great influence on the moment when the change of dominant initiating particle occurs, is observed. By using the value 2.26 × 10 ⁻³¹ cm ³ /s good agreement between simulation values and experimental data is obtained. Finally, the experimental data are fitted by the variation of effective diffusion coefficient, caused by the change of diffusion regime. In the time interval from 20–40 ms the value of effective diffusion coefficient is approximately equal to that determined by the approximate analytical model. These results from the numerical models are in good agreement with the results from the analytical model and measurements, thus confirming the basic conclusions about ion conversion and afterglow relaxation in argon at low pressure.