The effect of trapped energetic particles (EPs) on magnetohydrodynamics (MHD) modes has been comprehensively studied for decades. ^{[ 1 – 4 ]} The fishbone as an energetic particle mode (EPM) on the q = 1 rational surface, associated with the loss of fast ions, was first discovered in the poloidal divertor experiment (PDX) during high-beta operations with neutral beam injection (NBI). ^{[ 1 ]} This mode has a high frequency and a low frequency branch, corresponding to ω ≫ ω _* and ω ∼ ω _* respectively, ^{[ 5 – 9 ]} where ω _* is the ion diamagnetic frequency. It was shown that the precession and diamagnetic drift frequencies of the fast ions play an important role in destabilizing the mode. ^{[ 8 , 9 ]}

For the conventional magnetic shear regime, when the frequency of the mode is close to the fast ion precession frequency, ω ∼ ω _dh , fast ions can drive the instability significantly by Alfvén resonance. ^{[ 2 , 5 ]} The analytic study of this mode was first derived by Chen based on a generalized energy principle. ^{[ 2 ]} The dispersion relation of fishbone mode has been obtained as D ( ω ) = 0. If the mode frequency is close to ω _* , the low-frequency fishbone mode can be excited by ion diamagnetic drift, corresponding to the diamagnetic fishbone mode. ^{[ 8 ]} On the other hand, fast electron-driven fishbone-like mode has been observed during electron cyclotron resonance heating (ECRH) in tokamak experiments, such as DIII-D, ^{[ 10 ]} HL-2A, ^{[ 11 – 14 ]} and EAST. ^{[ 15 ]} For a positive magnetic shear, the fishbone instability can be excited, depending on q ′ = d q /d r at q = 1 surface. ^{[ 16 , 17 ]} Therefore, the q -profile effect may play an important role in the dynamics of the mode.

On the other hand, for the reversed magnetic shear regimes, the conventional fishbone analysis may be invalid to explain the fast ion driven modes. ^{[ 6 , 7 ]} While q ₀ , is close to unit, this mode has been observed with a non-monotonic q -profile in DIII-D, ^{[ 10 ]} NSTX, ^{[ 18 ]} and MAST. ^{[ 19 ]} The growth rate of the kink mode with the reversed magnetic shear given is also valid in q _min > 1 and 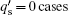. ^{[ 20 ]} In previous analysis, fishbone-like instabilities have been well understood both theoretically and experimentally, such as on off-axis heating, ^{[ 21 ]} plasma rotation, ^{[ 22 ]} non-ideal effect, ^{[ 23 – 25 ]} etc. However, the effect of current profile on the energetic ion-driven m = 1, n = 1 mode does not have a systematic investigation yet. ^{[ 4 ]} Thus, the studies of the mode with different q -profiles should be carried out, particularly to better understand the proprieties of the mode in ITER plasma with hybrid operation scenarios. ^{[ 17 ]}

In this paper, we apply ITER-like parameters and study the linear stability of the modes with different q -profiles. Including the diamagnetic effect, the numerical result for the modes with special parameters setting is in good agreement with the prediction of the linear theory. In addition, we also study the reserved shear mode with q _min > 1 and q _min < 1, and the main parameters of MHD and fast ion are discussed.

This rest of this paper is organized as follows. In Section 2, we discuss the theoretical model and the dispersion relation of the mode. In Section 3, the effects of monotonic or nonmonotonic q -profile on the mode are shown by numerical analysis, respectively. Finally, the discussion and conclusion are presented in Section 4.

We first outline the previous analysis of the q = 1 mode in the weak magnetic shear regime with a monotonic or a nonmonotonic q -profile respectively. The MHD potential energy and the kinetic contribution of trapped fast ions of the m / n = 1/1 mode are written as ^{[ 2 , 5 ]}

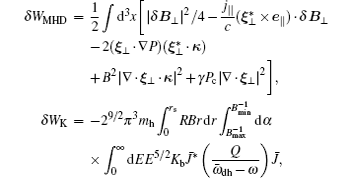
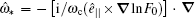
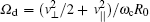
The dispersion relation in this case can be written as ^{[ 2 , 8 , 9 ]}

Fig. 1.

	Figure Option View Download New Window
	Fig. 1. Two types of q -profiles in different magnetic shear regimes, the monotonic q ( r ) = q 0 (1 + 0.8 r α ) 2 with the positive magnetic shear (the blue solid), and the nonmonotonic q ( r ) = q min + q c (1 − ( r / r m ) α ) 2 with a reversed magnetic shear (the red dashed).

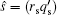
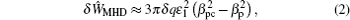
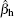
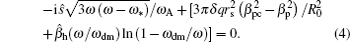
For the purely growing mode, ω = i γ , in the δ Ŵ _MHD = 0 case, the growth rate of the mode is

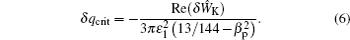
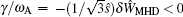
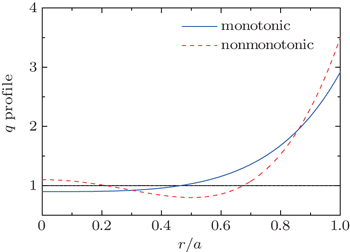
We assume that the q -profile is in the form of q ( r ) = q _min + q _c (1 − ( r / r _m ) ^α ) ² , where q ( r _m ) = q _min , as shown by the red dashed curve in Fig. 1 . The growth rate of the mode in this case can be given as ^{[ 18 ]}

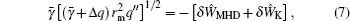
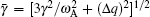
In the regime of q _min < 1, Δ q < 0, there are double rational surfaces of q = 1. For flattened q -profiles with a finite Δ q , the rational surfaces are far away from q = 1 and both current driven and the coupling of the two surfaces are very weak. For flattened q -profiles with a finite Δ q , the rational surfaces are far away from each other and both current driven and the coupling of the two surfaces are very weak. Then without EPs, the MHD branch of the mode is stable. Nevertheless, for a very small |Δ q |, the two resonant surfaces can be very close to each other and the MHD branch of the mode may become unstable. 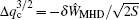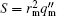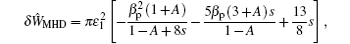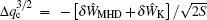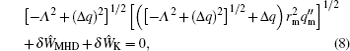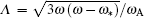The threshold Δ q can be given by with . For the very weak shear case of q ₀ − 1∼ ɛ , if the q = 1 surfaces are away from the magnetic axis, due to a small Δ q _c , the growth rate of the mode is found even larger than that of the internal kink mode with q ₀ < 1. The normalized MHD potential energy has a form of ^{[ 26 ]}

Numerical results of energetic particles driven q = 1 mode are represented in this section. In Subsections 3.1 and 3.2 we show results for monotonic and nonmonotonic q -profiles respectively, with a weak magnetic shear. In the calculation, we change the parameters of the q -profile in order to discuss the influence of a certain q -profile. Other parameters applied are ITER design parameters, with the major radius of R = 6.2 m and the minor radius of a = 2 m, and thus the inversed aspect-ratio ∼ 0.3. For the toroidal magnetic field B _T = 5.3 T and the density of plasma of n = 10 ²⁰ m ⁻³ , ^{[ 17 ]} we get the Alfvén frequency ω _A = V _A / R ₀ ≈ 1.3 × 10 ⁶ s ⁻¹ . For trapped energetic particles with an energy of E _m ∼ 1MeV, their toroidal precession frequency normalized by the Alfvén frequency is about ω _dm ≈ 0.01 ω _A . ^{[ 17 ]} For the ion diamagnetic effect, the typical ion diamagnetic frequency for ITER is about ω _* ≈ 0.001 ω _A . ^{[ 17 ]} The pressure profile we used in the numerical discussion is in a form of p ( r ) = p ₀ (1 − r ² ), and r is already normalized by minor radius. ^{[ 20 ]}

3.1. Weak magnetic shear monotonic q -profile

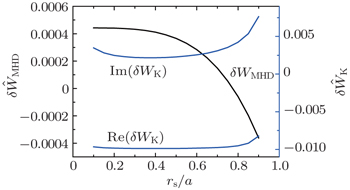
We first apply a monotonic q -profile in the form of q ( r ) = q ₀ (1 + 0.8 r ^α ) ² to approximate a profile of ITER plasmas. ^{[ 17 ]} There are two different ways to change the q -profile as shown in Fig. 2 . In Fig. 2(a) , we modify the central safety factor, q ₀ , from 0.92 to 0.98, and then vary the exponential parameter α with the q = 1 surface keeping at r _s = 0.3. In Fig. 2(b) , we keep q ₀ as a constant 0.98, and then vary α to move the q = 1 surface from 0.1 to 0.9. We then discuss these two cases separately as follows.

Fig. 2.

	Figure Option View Download New Window
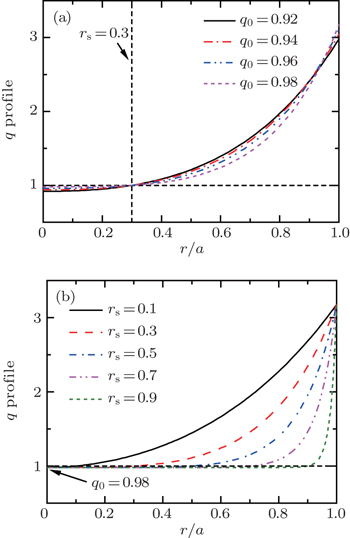	Fig. 2. Profiles of q ( r ) = q 0 (1 + 0.8 r α ) 2 . (a) r s = 0.3 with q 0 varying from 0.92 to 0.98, and (b) q 0 = 0.98 with r s varying from 0.1 to 0.9.

3.1.1. Fixing r _s and varying q ₀ , for q -profiles in Fig. 2(a)

The mode frequency and growth rate as a function of q ₀ are shown in Fig. 3 , with r _s = 0.3 for q ( r _s ) = 1, and q ₀ varying from 0.92 to 0.98. In Fig. 3(a) , it can be easily seen that the mode frequency for the MHD branch ( β _h = 0) is clearly distinguishable from that of the EP branch ( β _h ≠ 0). The mode frequency of the MHD branch is very small while for the EP branch ω _r ∼ ω _dm /2. ^{[ 2 ]} In Fig. 3(b) , it is seen that the MHD branch is stable with a very slowly varied negative growth rate, due to the fact that δ Ŵ _MHD ∼ 0. For the EP branch, the mode is obviously destabilized by energetic particles. The growth rate of the mode increases with both q ₀ and β _h , since the stabilizing effect of the MHD potential energy becomes weak as q ₀ increases and the destabilizing effect of EPs becomes strong as β _h rises. Another factor changing with the q -profile is the magnetic shear s on the rational surface, as plotted in Fig. 3(b) by the blue triangles. It is clearly seen that the mode growth rate rises as the magnetic shear falls. It shows that the magnetic shear also suppresses the mode. ^{[ 2 , 5 , 17 ]}

Fig. 3.

	Figure Option View Download New Window
	Fig. 3. The mode frequency (a) and growth rate (b) as a function of q 0 .

3.1.2. Fixing q ₀ and varying r _s , for q -profiles in Fig. 2(b)

The mode frequency and growth rate as a function of q ₀ are shown Fig. 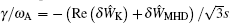3 , with a fixed q ₀ and a shifted r _s . The mode frequency of the EP branch shown in Fig. 4(a) falls fast as r _s increases, due to the significant drop of the toroidal precession frequency, while that of the MHD branch varies slowly with r _s . The growth rate of the mode is plotted in Fig. 4(b) . The MHD branch becomes unstable as the rational surface leaves the core region due to the fall of δ Ŵ _MHD as shown in Fig. 5 . However, the growth of the mode is very slow. For the EP branch, the growth of the mode slows down as the rational surface approaches the edge. It can be understood by the following discussion. For this case, the dispersion relation of the EP branch can be simplified as . It is seen in Fig. 5 that | δ Ŵ _MHD | ≪ | Re ( δ Ŵ _K )|, and Re ( δ Ŵ _K ) nearly remains constant. Thus, the growth rate variation depends mainly on the magnetic shear. As shown in Fig. 4(b) , the magnetic shear increases fast as the rational surface approaches the edge region.

Fig. 4.

	Figure Option View Download New Window
	Fig. 4. The mode frequency (a) and growth rate (b) as a function of r s .

Fig. 5.

	Figure Option View Download New Window
	Fig. 5. The MHD potential δ Ŵ MHD (black) and the energetic particle contribution δ Ŵ K (blue) as a function of r s .

3.2. Nonmonotonic q-profiles with a weak but reversed magnetic shear

In this subsection, we further discuss effects of the q -profile with reversed shears. The equilibrium q -profile is chosen as q ( r ) = q _min + q _c (1 − ( r / r _m ) ^α ) ² . In this kind of profile, the safety factor reaches its minimum q _min , at r = r _m , and q ₀ = q _min + q _c . We then explore the influence of such q -profile on the mode.

3.2.1. Varying the minimum value of safety factor q _min

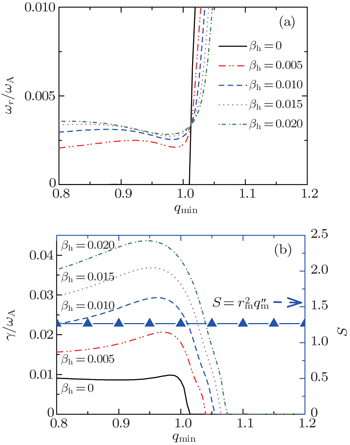
We lift the q -profile up entirely at first by changing q _min from 0.80 to 1.20 and fixing other parameters as q _c = 0.2, r _m / a = 0.5, and α = 2 as plotted in Fig. 6 .

Fig. 6.

	Figure Option View Download New Window
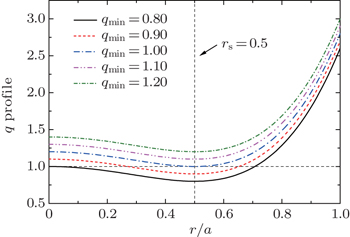	Fig. 6. Profiles of q ( r ) = q min + q c (1 − ( r / r m ) α ) 2 with q c = 0.2, r m = 0.5, α = 2, and a changing q min from 0.80 to 1.20.

The mode frequency and growth rate are shown in Fig. 7 . For both the MHD and fishbone branches, we can see clearly the differences between the resonant mode with two q = 1 resonant surfaces on both sides of r _m , for q _min < 1, and the non-resonant mode without the q = 1 resonant surface, ^{[ 18 ]} for q _min < 1. The resonant mode is clearly unstable with a high growth rate and a slow frequency, while the non-resonant mode is though unstable but with a slow growth rate and a fast frequency. The growth rate of the resonant mode rises with q _min , clearly resulting from the enhanced coupling between the two resonant surfaces as q _min increases. However, the growth rate of the non-resonant mode falls rapidly as q _min rises, resulting from the fact that the mode is more stable as q _min is farther away from the mode structure of m / n = 1.

Fig. 7.

	Figure Option View Download New Window
	Fig. 7. The mode frequency (a) and growth rate (b) as a function of q min .

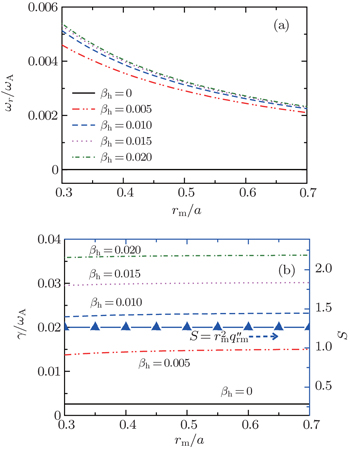
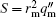
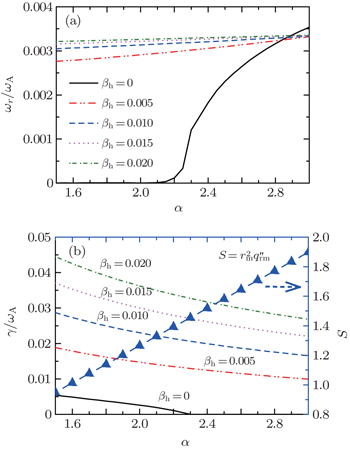
Moreover, at r = r _m , the safety factor reaches its minimum and the magnetic shear ŝ = rq ′/ q vanishes. We therefore introduce a modified magnetic shear by taking the second derivative of the safety factor function to estimate the magnetic field line bending effect as . Nevertheless, the modified shear S stays constant in this case. Then we will see its effect in the following discussion.

3.2.2. Varying the exponential parameter α

Thus we keep q _min = 1.01, q _c = 0.2, r _m / a = 0.5, and vary the parameter α only, to focus on the effect of the profile shape on the mode, as shown in Fig. 8 . The mode frequency and growth rate are then plotted in Fig. 9 . Clearly, the more flattened the q -profile is (for the smaller α ), the more unstable the mode will be. Particularly, there is a critical α _c ≈ 2.3, the MHD branch of the mode is unstable with a zero or a very slow frequency for α < α _c , and stable with a fast rising frequency for α > α _c . For the EP branch, it is again shown that EPs in the reversed magnetic shear regime destabilize the mode.

Fig. 8.

	Figure Option View Download New Window
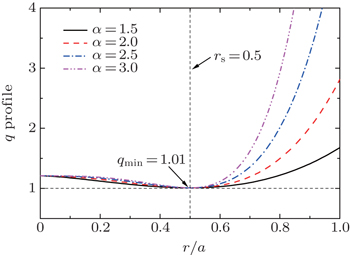	Fig. 8. Profiles of q ( r ) = q min + q c (1 − ( r / r m ) α ) 2 with q c = 0.2, r m = 0.5, q min = 1.01, and a changing α from 1.5 to 3.0.

Fig. 9.

	Figure Option View Download New Window
	Fig. 9. The mode frequency (a) and the growth rate (b) as a function of α .

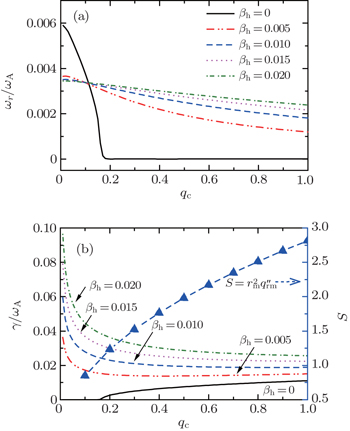
The magnetic field line bending effect influenced by the modified magnetic shear S is the main stabilizing mechanism of the mode. We see that S increases with α . Therefore, the mode growth rate of the EP branch falls as α increases.

3.3. Varying the location of r _m

We then fix q _c = 0.2, α = 2, and q _min = 1.01, but only change r _m from 0.3 to 0.7, as plotted in Fig. 10 . It is seen clearly in Fig. 11 , the features of the mode, except for the mode frequency of the EP branch, do not vary much with r _m , a fact that indicates that the mode characteristics depend largely on the local profile shape, rather than the location of q _min surface.

Fig. 10.

	Figure Option View Download New Window
	Fig. 10. Profiles of q ( r ) = q min + q c (1 − ( r / r m ) α ) 2 with q c = 0.2, α = 2, q min = 1.01, and a changing r m from 0.3 to 0.7.

Fig. 11.

	Figure Option View Download New Window
	Fig. 11. The mode frequency (a) and growth rate (b) as a function of r m .

3.3.1. Varying the factor q _c = q ₀ − q _min

The q -profiles with q _c changing but other parameters fixed are shown in Fig. 12 . The factor q _c noticeably has an effect on shaping the q -profile similar to that of the exponential parameter of α . Thus, the influence of q _c on the mode is also similar to it. A critical q _cc ≈ 0.16 is found for the MHD branch in Fig. 13 . As q _c increases, the MHD branch of the mode is unstable with a zero frequency for q _c > q _cc , and stable with a fast rising frequency for q _c < q _cc . Nevertheless, since the modified magnetic shear varies significantly with q _c , the effect of q _c on the mode is thus more substantial than that of the parameter of α .

Fig. 12.

	Figure Option View Download New Window
	Fig. 12. Profiles of q ( r ) = q min + q c (1 − ( r / r m ) α ) 2 with r m = 0.5, α = 2, q min = 1.01, and a changing q c from 0 to 1.0.

Fig. 13.

	Figure Option View Download New Window
	Fig. 13. The mode frequency (a) and growth rate (b) as a function of q c .

In this paper, we have studied the effect of q -profile on the linear stability of the q = 1 mode with different regimes of the magnetic shear. The dispersion relation of the mode is given by a modified fishbone model for both monotonic and nonmonotonic q -profiles. For ITER-like parameters, we calculated the dispersion relation of the mode and make a comparison with theory. It is found that the current profile, i.e., the q -profile, can significantly change the stability feature of the mode. The EP-dominant instability excited at the q = 1 surface is tested numerically. The non-resonant mode with q _min > 1 due to the pure fast ion driven is also numerically studied for different types of q -profiles with key parameters varying respectively. It is found that there are two main factors influencing the instability significantly, the MHD potential energy and the magnetic shear. The MHD potential is affected by many factors, such as the central safety factor, the minimum safety factor, and the location of rational surface etc. As for the magnetic shear, it plays an important role in stabilizing both the MHD and the EP branches in the weak magnetic shear regime.