Cite this Article
Wei Wei, Ding Bo-Jiang, Peysson Y, Decker J, Li Miao-Hui, Zhang Xin-Jun, Wang Xiao-Jie, Zhang Lei. Optimized calculation of the synergy conditions between electron cyclotron current drive and lower hybrid current drive on EAST. Chinese Physics B , 2016, 25(1): 015201  
Permissions
Optimized calculation of the synergy conditions between electron cyclotron current drive and lower hybrid current drive on EAST
Wei Wei 1, 2 , Ding Bo-Jiang 2, †, , Peysson Y 3 , Decker J 3 , Li Miao-Hui 2 , Zhang Xin-Jun 2 , Wang Xiao-Jie 2 , Zhang Lei 4
Hefei University of Technology, Hefei 230009, China
Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China
CEA, IRFM, 13108 St. Paul-lez-Durance, France
Shanxi University of Technology, Hanzhong 723001, China

 

† Corresponding author. E-mail: bjding@ipp.ac.cn

Project supported by the National Magnetic Confinement Fusion Science Program of China (Grant Nos. 2011GB102000, 2012GB103000, and 2013GB106001), the National Natural Science Foundation of China (Grant Nos. 11175206 and 11305211), the JSPS-NRF-NSFC A3 Foresight Program in the Field of Plasma Physics (Grant No. 11261140328), and the Fundamental Research Funds for the Central Universities of China (Grant No. JZ2015HGBZ0472).

Abstract
Abstract

The optimized synergy conditions between electron cyclotron current drive (ECCD) and lower hybrid current drive (LHCD) with normal parameters of the EAST tokamak are studied by using the C3PO/LUKE code based on the understanding of the synergy mechanisms so as to obtain a higher synergistic current and provide theoretical reference for the synergistic effect in the EAST experiment. The dependences of the synergistic effect on the parameters of two waves (lower hybrid wave (LHW) and electron cyclotron wave (ECW)), including the radial position of the power deposition, the power value of the LH and EC waves, and the parallel refractive indices of the LHW ( N ∥ ) are presented and discussed.

PACS : 52.35.Hr ; 52.55.Fa ; 52.65.–y ; 52.65.Ff
Keyword : EAST ; lower hybrid current drive (LHCD) ; electron cyclotron current drive (ECCD) ; synergistic effect
1. Introduction

Both the lower hybrid current drive (LHCD) and electron cyclotron current drive (ECCD), as two important ways of non-inductive current drive in tokamak, have advantages and disadvantages. The greatest advantage of LHCD is the high current drive efficiency, because it can directly increase the parallel velocity of current-carrying electrons through Landau damping. Its main drawbacks are difficulty of current profile control and accessibility problem at high density. Compared with LHCD, the ECCD is widely used to control the plasma current profile and suppress the plasma MHD activity due to easy coupling, strong localization, and controllable absorption. However, the disadvantage of the ECCD is the low current drive efficiency, because it is drive current indirectly through cyclotron damping which causes resonant electrons to obtain energy and an increase of the perpendicular velocity.

Owing to these complementary features, a combination of LHCD and ECCD becomes an appealing solution for high-performance and long-pulse advanced tokamak discharges. Fidone first proposed in the 1980’s [ 1 ] that the I EC+LH , which is defined as the total current driven by the ECW and LHW simultaneously, is larger than the sum ( I EC + I LH ) of the currents driven by the ECW and LHW separately, i.e., I EC+LH > I EC + I LH . Since then, theoretical and experimental studies of the synergy have been carried out in many devices, such as WT-2, [ 2 ] JFT-2M, [ 3 ] WT-3, [ 4 ] Versator II, [ 5 ] etc. In addition, several Fokker–Planck codes [ 6 – 8 ] have numerically demonstrated this phenomenon. However, the results of these experiments could not provide a quantitative assessment of the synergistic effect. In 2004, the first experimental verification of the synergy between LHCD and ECCD was obtained on Tore Supra, [ 9 ] and this experiment still needs further physical explanation. Therefore, it is necessary to study the physical mechanism of the synergistic effect, which will provide a theoretical direction, and the optimized synergy conditions for the synergy experiments will be carried out on the EAST.

2. Kinetic modeling and C3PO/LUKE code

At present, it is considered that the synergistic effect is caused by the synergy electrons arising from the two waves in the phase space. [ 10 ] The so-called synergy electrons are those high-energy electrons, each of which obtains a higher vertical velocity u ⊥ and parallel velocity u ∥ by interacting with ECW (or LHW), and thus enters the LHW (or ECW) resonant region. The current driven by these high-energy electrons is the additional synergy current generated during the synergy period. It is generally considered that there are two mechanisms of the synergetic effect: (i) the electrons are first pushed by the ECCD, and then be further driven by the LHW as long as they enter the LHCD resonant region; and (ii) the electrons are first dragged by the LHCD, and then the ECW could selectively couple with the fast electron tail sustained by the LHW.

The codes used to obtain LH+EC wave absorption and LH+EC synergy current are GENRAY [ 11 ] /CQL3D, [ 7 ] FRTC [ 12 ] /OGRAY [ 8 ] and C3PO [ 13 ] /LUKE. [ 6 ] In this study, the C3PO/LUKE code is used. The LUKE is a code for solving the three-dimensional (3D) (two-dimensional (2D) momentum and one-dimensional (1D) radial) bounce-averaged relativistic electron drift kinetic equation for the absorption of the waves by the electrons, which is coupled to the ray-tracing solvers C3PO for the wave propagation. It is designed for the current drive problem of any RF electron wave (LH, EC, electron Bernstein waves) in tokamak with an arbitrary axisymmetric magnetic equilibrium. The C3PO/LUKE code can be used to simulate ECRH/ECCD, as well as synergistic effects with other electron waves such as LHCD in a consistent way.

In the following, we discuss the kinetic modeling of LH+EC current drive. Current drive by superthermal electrons is numerically investigated using the 3D linearized relativistic bounce-averaged electron Fokker-Planck equation: [ 6 , 14 , 15 ]

where f ( r , p , ξ 0 , t ) is the electron distribution function at the radial location r and time t ; p is the electron momentum; and ξ 0 is the pitch angle cosine at the minimum of the magnetic field on a magnetic flux surface; v gc is the guiding center velocity; C ( f ), Q ( f ), and ε ( f ) are the collision operator, quasilinear operator, and electric field operator, respectively, which can be given by

with S C , S W , and S E being the Coulumb collisions (C), radio frequency (rf) wave (include LHW and ECW), and Ohmic electric field (E) induced electron fluxes, respectively.

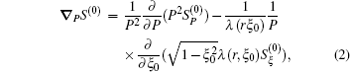
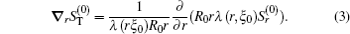
The flux divergences of the momentum and radial space in the kinetic equation ( 1 ) can be expressed in conservative form as

and

The superscript “(0)” represents the bounce averaged, λ is the normalized bounce time, and S T is the electronic radial diffusion transport (T) induced electron flux.

The phase space flux S (0) is decomposed into a diffusive term and a convective term, i.e., S (0) = − D (0) ∇ f (0) + F (0) f (0) . Here, D (0) and F (0) are respectively the diffusion tensor and convection vector in phase space. The bounce averaged flux of Eqs. ( 2 ) and ( 3 ) are given by

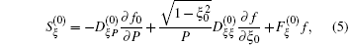
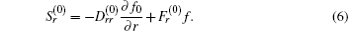
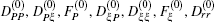
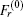
These coefficients , and need to be determined separately in the process of calculation for different physical terms (LH, EC, C, E, T). The radio frequency (RF) wave terms (LH, EC) are purely diffusive so that , while the electric field term (E) is purely convective, .

For the RF wave terms (LH, EC), corresponding diffusion tensors which depend on the waves present in the plasma and are based on the quasilinear theory of the interactions between waves and plasmas can be expressed as follows:

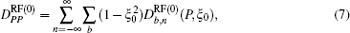
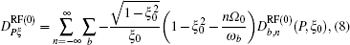
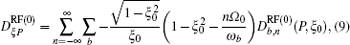
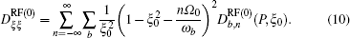
Here, 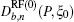is the quasi-linear diffusion coefficient which describes the interaction of the electrons with a given beam b at an harmonic number n , Ω 0 is the cyclotron frequency taken at the minimum value of magnetic field, and ω b is the wave frequency. For lower hybrid wave, we have n = 0 and the quasilinear diffusion is strictly along the parallel direction (i.e., magnetic field line). For simplicity, at a cyclotron harmonic, where ω b = nΩ ( Ω is the cyclotron frequency), the perpendicular diffusion is only taken into account. Here a parallel component, which may exist if the wave is launched at a non-zero angle toroidally, and relativistic corrections are not considered.

The detailed expressions of other coefficients for different physical terms (C, E, and T) can be found in Ref. [ 6 ].

The current density carried by electrons associated with f can be calculated by

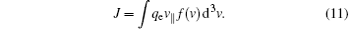
The RF power absorbed per unit volume by the plasma is given by

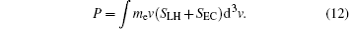
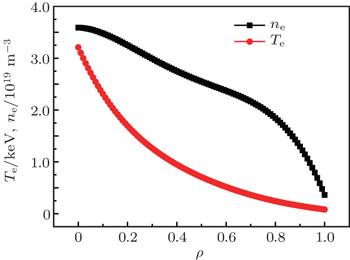
3. Calculation results with the parameters of EAST

EAST is a full superconducting tokamak device with non-circular cross section. The typical background plasma parameters are as follows: plasma major radius R = 1.85 m, plasma minor radius a = 0.45 m, plasma elongation ratio κ = 1.9, and triangle variable factor δ = 0.5. The working frequency of the ECRH system is chosen to be 140 GHz and the second harmonic extraordinary mode (X2) is used for electron heating and current drive. The wave source is amplified by 4 gyrotrons each with 1 MW/100 s output power. A total power of 4 MW is injected into the plasma through the horizontal port from the low field side. The radius of the launch point of the EC wave R a is 300 cm, and the vertical deviation of the launch point with respect to the middle plane Z a is 30 cm.

In order to compare with the experimental results better, the parameters adopted in this calculation are given as plasma current I P = 400 kA, toroidal magnetic field Bt 0 = 2.3 T, lower hybrid wave (LHW) frequency f LH = 4.6 GHz, LHW power P LH = 2 MW, and the peak value of parallel refractive index 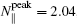, which are the parameters for discharge #48888 of the full wave current drive by 4.6 GHz LHW in the 2014 EAST experiment. In this paper, plasma equilibrium is simulated by the EFIT code. [ 16 ] The profiles of electron density n e and electron temperature T e have been used are also the measurement results in the discharge #48888 (see Fig. 1 ).

Fig. 1. Radial profiles of electron density and electron temperature used in this paper.
3.1. Dependence of synergistic effect on radial position of the power deposition

In order to investigate the effect of radial position of the power deposition on the synergistic effect between ECCD and LHCD, the radial position of the peak drive current density of the LHW is fixed to be ρ LH = 0.05. At the same time, a movable mirror is used to adjust the toroidal or poloidal incident angle of the EC wave antenna, hence changing the radial position of ECW power deposition. The synergistic effects at different values of radial position ρ EC (in normalized radius) at which the EC current is driven are investigated by scanning the poloidal injection angle θ and toroidal injection angle φ of ECW. The calculation results are shown in Fig. 2 , where the ECW and LHW power are 1 MW and 2 MW, respectively. From Fig. 2 , it is shown that the radial positions of ρ EC and ρ LH are the key factors affecting the synergy effects. When ρ EC is close to ρ LH , a greater synergy current (defined as I syn = I EC+LH − I EC − I LH ) I syn = 207 kA and synergy factor (defined as F syn = I EC+LH /( I EC + I LH ) [ 10 ] ) F syn = 1.428 can be obtained as shown in Fig. 2(a) . With the position of ρ EC starting far from ρ LH , the synergistic effect still exists because the ECW is still deposited at the LHW absorption edge region, but the synergy current and synergy factor are reduced gradually. Figure 2(d) shows that when ρ EC is far from ρ LH , the profile of driven current density with ECW+LHW is very similar to that of LHW alone. Here, the synergistic effect is very poor ( I syn = 19.3 kA, F syn = 1.042).

Fig. 2. Profiles of driven current density with [(a1), (a2)] ECW only, [(b1), (b2)] LHW only, and [(c1), (c2)] ECW+LHW, and [(d1), (d2)] the comparisons of the synergistic effect between ECCD and LHCD at different values of ρ EC .

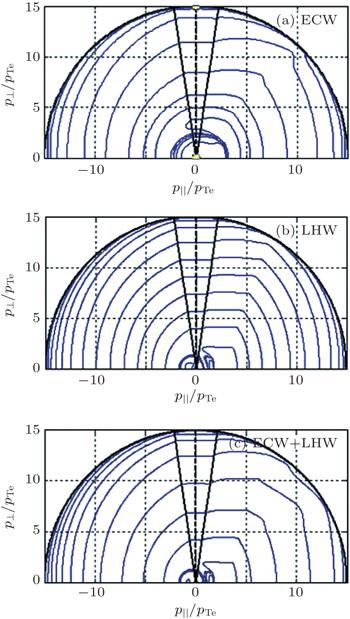
In order to obtain a larger synergistic effect, the first condition is to make the peaks of the drive current density of the LHW and ECW overlap. Furthermore, the diffusion regions of the two waves in the velocity space must also overlap. Figure 3 shows the interaction between two waves and electrons in velocity space. Generally, the role of the ECW is to push electrons to a higher vertical velocity and obtain the greater vertical energy by the cyclotron damping. In addition, the role of LHW is to push electrons to a higher parallel velocity and obtain the greater parallel momentum by the Landau damping. Figure 3(c) shows that the electrons obtain a larger parallel and vertical momentum after combining with two waves, and this is no simple linear superposition. In fact, the low energy electrons are accelerated by the ECW and obtain a higher vertical velocity, which can fall into the lower limit of the LHW resonance region, and will obtain a greater parallel velocity due to a further acceleration by the LHW. Furthermore, these electrons are far from the electron trapping region because of the large parallel speeds. Therefore, a larger synergy current drive by two waves than by LHW and ECW separately can effectively be obtained.

Fig. 3. Deviations of electron distribution function from the Maxwellian by (a) ECW only, (b) LHW only, and (c) ECW+LHW at ρ = 0.05. p ⊥ and p ∥ are the relativistic momentum components perpendicular and parallel to the magnetic field.

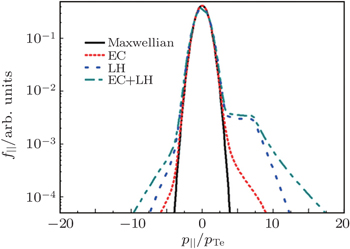The electron distribution functions before and after inputting the EC or LH waves [ 17 ] are shown in Fig. 4 . As is well known, the initial plasma is of a symmetric Maxwell distribution. The wave interacts with the electrons by cyclotron damping or Landau damping after inputting the ECW or LHW, thus a steady distortion distribution (i.e., an asymmetric electron distribution function) can form and the non-inductive current can be driven continuously during the ECW or LHW application. By solving the Fokker–Planck equation, four cases of electron distribution functions (Maxwellian, ECW alone, LHW alone and LHW+ECW) at normalized radius ρ = 0.05 are obtained. It is seen that the high-energy plateau with the LHW+ECW considered is more prominent than with LHW alone, thereby leading to a higher driven current.

Fig. 4. Parallel distribution functions with Maxwellian, ECW only, LHW only, and ECW+LHW at ρ = 0.05.

In conclusion, there is a strong dependence of the synergistic effect between LHCD and ECCD on the power deposition locations of the two waves. A larger synergistic effect could be obtained when the peaks of the ECW and LHW current density are superposed, because this may further make the two waves overlap in the velocity space, and the overlapping of the diffusion regions of ECW and LHW can make the high-energy electrons accelerated by one kind of wave accelerate, and further by another wave, and then an additional synergistic current can be formed effectively. The power deposition position of the LHW is mainly determined by LHW power spectrum, profiles of plasma temperature and density, which are generally difficult to adjust. However, the change of the location of the ECW can be easily realized by adjusting the toroidal and poloidal incident angle of the ECW antenna. Therefore, in order to obtain a better synergistic effect, the ECW power is arranged to deposit at the same radial position of the LHW power by selecting appropriate toroidal and poloidal inject angles of the ECW. The relationships between the ECW parameters and its deposition position have been studied in detail in Ref. [ 18 ].

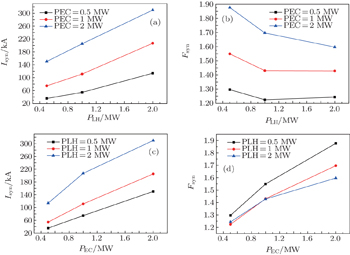
3.2. Dependences of synergistic effect on ECW power and LHW power

The relationship between the synergistic effect and the powers of ECW and LHW has been studied numerically and experimentally in many fusion devices. Research shows that the fraction of the trapped electrons, the changes of the local temperature, [ 7 ] the profile of the wave power deposition and its absorption position [ 19 ] are affected strongly by the levels of the powers of the two waves, which make the synergy current change, even lower than zero, i.e., a negative synergy effect ( I EC+LH < I EC + I LH ) can be obtained when the ratio between the powers of the two waves satisfies a certain condition. [ 20 , 21 ] Therefore, it is necessary to study the dependences of the synergistic effect on ECW power and LHW power in the EAST to avoid the negative synergy effect, which is meaningful for guiding the relevant physical experiments in the future.

The synergy currents are investigated with the LHW and ECW power scanning from 0.5–2 MW, respectively. The calculation results are shown in Fig. 5 . It is seen that the synergistic effect is much more dependent on the level of EC wave power: the synergy current and synergy factor increase obviously with the increase of ECW power. In addition, at the levels of 0.5–2 MW of ECW and LHW power, the synergy currents vary linearly with the LHW and ECW power with no negative synergy effect. The calculations by the C3PO/LUKE code on the EAST indicate that the maximum synergy current I syn is about 300 kA, synergy factor F syn is about 1.9, and the total current driven by the ECW and LHW I EC+LH is about 830 kA, when P LH = 2 MW and P EC = 2 MW.

Fig. 5. Synergistic effect as a function of the input power. (a), (b) Synergy current and synergy factor versus LHW power at different ECW powers; (c), (d) synergy current and synergy factor versus ECW power at different LHW powers.

The mechanism of current enhancement caused by the synergy of two waves can be qualitatively explained as follows. [ 22 ] First, the application of ECW leads to the increase of the fast electron population, and the effect of Landau damping of the LHW is improved. Then the local electron temperature increases because of the ECW, which will reduce the collision frequency between the resonant electrons and background ions (the collision frequency is proportional to ), and the plasma current carried by fast electrons is increased indirectly. Therefore, the effect of ECW power on the synergistic effect is very strong: with the increase of ECW power, not only does the number of fast electrons increase, but also the collision frequency decreases due to the increase of the local electron temperature, which induces the synergistic effect to become better. In Ref. [ 19 ] it was also pointed out that the EC power level is a very important parameter for synergy current, especially for the profile of the power deposition of LHW. As the ECW power increases, the peak of absorption for LHW moves towards the barrier region. As a consequence there is a strong increase in the combined current drive, and synergy effects produce higher current drive efficiency than would be attained if the current drive efficiencies of LH and EC waves were independent of each other.

Figure 6 shows the variations of the synergy current and synergy factor with the P EC / P LH power ratio. With the increase of P EC / P LH , i.e., increasing the proportion of the ECW power, the synergistic effect becomes better, which also shows the important influence of ECW power on the synergistic effect. However, figure 6 also shows such a phenomenon that the synergy effect decreases with the increase of the LHW power ratio. The reasons may be that the confinement of current-carrying superthermal electrons becomes poor and the radial transport is enhanced with the increase of the LHW power ratio.

Fig. 6. Variations of synergy current (a) and synergy factor (b) with P EC / P LH power ratio.
3.3. Dependence of synergistic effect on N ∥ of LHW

The parallel refractive index of LHW ( N ∥ ) is an important parameter for LHCD, which determines the properties of the LHCD experiment, such as the coupling of the wave to the plasma, the propagation of the LHW, the LHW power deposition, the driven current profile, as well as the current drive efficiency, and then will affect the synergistic effect simultaneously.

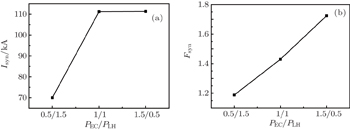
In order to study the dependence of the synergistic effect on N ∥ of the LHW on the EAST, the comparisons of the synergistic effect among three cases of , 2.2, 2.4 are given in Fig. 7 . It shows that the best synergistic effect is obtained at , followed by and . This may lie in the fact that the drive efficiency depends on the parallel index of refraction of the LHW. By simulation, the current driven by the LHW (2 MW) only, when is 457 kA, is greater than the LHCD current in the case of ( I LH = 436 kA) and ( I LH = 356 kA) (see Fig. 8 ). This result indicates that the synergistic effect strongly depends on the driven current of LHW. As its current drive efficiency is one order higher than that of the ECW, the LHW plays an important role in the synergy current drive. In the phase of ECCD and LHCD synergy current drive, a higher LHCD efficiency means that more fast electrons are driven and they can be accelerated further by ECW to obtain a larger synergy current. The dependence of LHCD efficiency on N ∥ is very significant, because N ∥ determines not only the location of LHW power deposition, but also the velocity component of the high energy electron group interacting with the LHW.

Fig. 7. Variations of synergy current (a) and synergy factor (b) with .
Fig. 8. Current driven by the LHW versus .

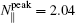
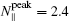
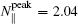
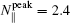
The resonant condition of the LHW, according to ω − k ∥ v ∥ = 0, [ 23 ] where ω is the LHW frequency, v ∥ and k ∥ = N ∥ ω / c are the parallel components of the velocity of the resonant electrons and wave vector of the LHW, respectively, can be written in the form of

where v Φ ∥ is the parallel phase velocity of the LHW. We can see from formula ( 13 ) that when N ∥ is smaller, which means that the phase velocity of the LHW is relatively greater, most of the wave beams interact with the electrons close to the core plasma. With the increase of N ∥ , the wave phase velocity decreases, thus more edge electrons with enough speed can interact with LHW and acquire the energy from the wave. Since the density and the temperature in the edge plasma are lower than in the core region, the LHCD efficiency will decrease with the increase of N ∥ . However, the LHW cannot propagate through the plasma if the N ∥ is too small due to the accessibility condition.

On the other hand, N ∥ of the LHW determines the resonance and position of the LHW, then it will affect the production of the synergy electrons. Figure 9 shows that with N ∥ increasing from 2.04 to 2.4, the resonance region of the LHW gradually moves from the high v ∥ to the low v ∥ region. At the same time, the overlapping region of the two waves gradually becomes smaller. According to the synergistic effect mechanism, when the resonant regions of the LH and EC waves have a common area in the velocity space, the synergy electrons can be produced, which is the necessary condition for producing the synergy current, because only when the two wave resonance regions overlap, can the high energy electrons driven by LHW fall into the resonance region of ECW and further be accelerated by ECW to obtain a greater vertical speed and become a synergy electron. The additional current can then form effectively.

Fig. 9. Resonances of the EC and LH waves for values of 2.04 (a), 2.2 (b), and 2.4 (c).

In a word, the synergistic effect is better when the LHW with an appropriate N ∥ that can drive a larger current and can make the resonance area of the two waves in the velocity space overlap combines with the ECW.

4. Conclusions and discussion

Numerical simulation of the synergistic effect between LHCD and ECCD is systematically done and investigated by C3PO/LUKE in EAST tokamak. By simulation, we study the dependence of the synergistic effect on the power deposition locations of ECCD and LHCD, the power level of the two waves, and the parallel refractive indices of the LHW. In order to obtain a better synergistic effect, the peaks of the drive current density of the LHW and ECW must be overlapped, because this may further make the diffusion region of two waves overlap in the velocity space. We usually adjust the poloidal or toroidal incident angle of the ECW to deposit the ECW power at the same radial position of the LHW to obtain a good synergistic effect. Furthermore, the synergistic effect is much more dependent on the levels of EC and LH wave power. Moreover, as the powers of the two waves increase, the synergy currents vary linearly with the LHW and ECW power at the power levels of 0.5–2 MW on the EAST, the maximum total current driven by the ECW and LHW simultaneously and synergy current calculated by the C3PO/LUKE code on EAST are about I EC+LH = 830 kA and I syn = 300 kA with P LH = 2 MW and P EC = 2 MW, respectively. However, in this paper we neglect the change of the electron temperature T e profile (and the density). While in the real experiment, the plasma temperature and density change with the values of LHW and ECW power, which can also affect the influence of the tail of the distribution function of the electrons on the synergistic effect. Finally, since LHCD current and the resonant position are significantly affected by N ∥ , an important parameter for the synergistic effect.

Note that the present simulation is preliminary and to investigate the synergy effect for a given LH power deposition by modifying EC wave parameters so as to gain a large driven current. Such simulation results depend on LH power deposition, which is related to the LH model, e.g., effects of spectrum broadening on power deposition. In this paper, we only consider the case of power deposition with the LH model without considering spectrum broadening. In addition, note that high power injection (e.g., 4 MW) will strongly modify the plasma, and radial transport may totally cancel the effects if anomalous transport is too high. The tail of the distribution function of the electrons cannot be built, and the synergy will drop. Therefore, the role of power scanning is only to see the change tendency of the synergy effect. Further work will be performed by comparing experiments and LH simulation where a more reasonable LH model is applied.

Reference
1 Fidone I Giruzzi G Granata G Meyer R L 1984 Plasmas. Phys. Fluids 27 2468
2 Ando A Ogura K Tanaka H Iida M Ide S Oho K Ozaki S Nakamura M Cho T Maekavva T Terumichi Y Tanaka S 1986 Phys. Rev. Lett. 56 2180
3 Yamamoto T Hoshino K Kawashima H Uesugi Y Mori M Suzuki N Ohta K Matoba T Kasai S Kawakami T Maeno M Matsuda T Matsumoto H Miura Y Ochiai I I Odajima K Ogawa T Ogawa H Ohtsuka H Sengoku S Shoji T Tamai H Tanaka Y Yamamoto S Yamauchi T Yanagisawa I I 1987 Phys. Rev. Lett. 58 2220
4 Maekawa T Maehara T Minami T Kishigami Y Kishino T Makino K Hanada K Nakamura M Terumichi Y Tanaka S 1993 Phys. Rev. Lett. 70 2561
5 Colborn J A Squire J P Porkolab M Villasen̄or J 1998 Nucl. Fusion 38 783
6 Decker J Peysson Y 2004 Euratom-CEA Report EUR-CEA-FC-1736
7 Harvey R W McCoy M G 1992 Proc. IAEA Technical Committee Meeting on Advances in Simulation and Modeling of Thermonuclear Plasmas, Montreal, Canada 489
8 Zvonkov A V Kuyanov A Y Skovoroda A A Timofeev A V 1998 Plasma Phys. Rep. 24 389
9 Giruzzi G Artaud J F Dumont R J Imbeaux F Bibet P Berger-By G Bouquey F Clary J Darbos C Ekedahl A Hoang G T Lennholm M Maget P Magne R Ségui J L 2004 Phys. Rev. Lett. 93 255002
10 Chen S Y Hong B B Liu Y Lu W Huang J Tang C J Ding X T Zhang X J Hu Y J 2012 Plasma Phys. Control. Fusion 54 115002
11 Smirnov A P Harvey R W 1995 Bull. Am. Phys. Soc. 40 1837
12 Esterkin A Rand Piliya A D 1996 Nucl. Fusion 36 1501
13 Peysson Y Decker J 2008 Euratom-CEA Report EUR-CEA-FC-1738
14 Charles Karney F F 1986 Computer Phys. Rep. 4 183
15 Zheng P W Gong X Y He L H Du D 2011 Progress Report on China Nuclear Science & Technology 2 56
16 Lao L L Ferron J R Groebner R J Howl W John H St Strait E J Taylor T S 1990 Nucl. Fusion 30 1035
17 Ding B J Zhang G R Li M H Zhang L Kong E H Zhang X J Qin C M Liu F K Shan J F Zhao Y P Wan B N 2011 Plasma Phys. Control. Fusion 53 065018
18 Wei W Ding B J Zhang X J Wang X J Li M H Kong E H Zhang L 2014 Chin. Phys. B 23 055201
19 Rosa P R da S Ziebell L F 2002 Plasma Phys. Control. Fusion 44 2065
20 Lu W Chen S Y Tang C J Bai X Y Zhang X J Hu Y J 2013 Chin. Phys. Lett. 30 065203
21 Chen S Y Tang C J Zhang X J 2013 Chin. Phys. Lett. 30 065202
22 Fidone I GiruzziI G Krivenski V Mazzucatoe E Ziebell L F 1987 Nucl. Fusion 27 579
23 Zhu S Y 1992 Principle of Nuclear Fusion Hefei University of Science and Technology of China Press 240