Cite this Article
Wang Lin-Li, Fu Jing-Li. Non-Noether symmetries of Hamiltonian systems with conformable fractional derivatives. Chinese Physics B , 2016, 25(1): 014501  
Permissions
Non-Noether symmetries of Hamiltonian systems with conformable fractional derivatives
Wang Lin-Li , Fu Jing-Li
Institute of Mathematical Physics, Zhejiang Sci-Tech University, Hangzhou 310018, China

 

† Corresponding author. E-mail: sqfujingli@163.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 11272287 and 11472247), the Program for Changjiang Scholars and Innovative Research Team in University, China (Grant No. IRT13097), and the Key Science and Technology Innovation Team Project of Zhejiang Province, China (Grant No. 2013TD18).

Abstract
Abstract

In this paper, we present the fractional Hamilton’s canonical equations and the fractional non-Noether symmetry of Hamilton systems by the conformable fractional derivative. Firstly, the exchanging relationship between isochronous variation and fractional derivatives, and the fractional Hamilton principle of the system under this fractional derivative are proposed. Secondly, the fractional Hamilton’s canonical equations of Hamilton systems based on the Hamilton principle are established. Thirdly, the fractional non-Noether symmetries, non-Noether theorem and non-Noether conserved quantities for the Hamilton systems with the conformable fractional derivatives are obtained. Finally, an example is given to illustrate the results.

PACS : 45.10.Hj ; 02.30.Xx ; 11.10.Ef
Keyword : conformable fractional derivative ; Hamilton’s canonical equation ; non-Noether conserved quantity
1. Introduction

The subject of symmetries plays a prominent role in physics, life sciences, and engineering. Using the symmetry theories to study the conservation laws is a recent development direction in mathematical physics. The symmetry theory mainly covers Noether symmetry, Lie symmetry, and Mei symmetry. Noether symmetry is an invariance of the Hamiltonian’s action under the infinitesimal transformations of groups. [ 1 ] Lie symmetry is an invariance of differential equations under the infinitesimal transformations of groups. [ 2 ] Mei symmetry means that the form of the equations of motion remains invariant under the infinitesimal transformations of groups for the state parameter. [ 3 , 4 ] In 1992, a theorem regarding the conserved quantities for second-order dynamical systems has recently been given by Hojman, [ 5 ] and generalized by Gonzalez-Gascon, [ 6 ] using geometric techniques. Subsequently, the generalized theorem of a velocity-dependent symmetry is presented by Lutzky. [ 7 ] Lately, Mei has studied the non-Noether conserved quantities for the Hamiltonian system in phase space. [ 8 , 9 ] Fu et al . developed a new non-Noether conserved quantity for Hamilton canonical equations. [ 10 ] Fang et al . gave a directive method to find the non-Noether conserved quantity. [ 11 ] In recent years, the symmetry theories with fractional calculus are carried out. Zhou et al . studied the symmetry theories of Hamiltonian systems with Riemann–Liouville fractional derivatives. [ 12 ] Zhang et al . investigated the Hamilton formalism and Noether symmetry for mechanico-electrical systems with fractional derivatives. [ 13 ] Zhou et al . gave Noether’s theorems of a fractional Birkhoffian system within Riemann–Liouville derivatives. [ 14 ] Sun et al . presented Lie symmetry theorem of fractional nonholonomic systems. [ 15 ]

For fractional systems, the Riemann–Liouville (RL) and Caputo fractional derivatives are popular among mathematicians and physicists. [ 16 – 31 ] For example, Riewe has developed a new approach to mechanics, and obtained a version of the Euler–Lagrange equations to problems of the calculus of variations with fractional derivatives for the dynamical systems. [ 32 , 33 ] Agrawal further presented the fractional variational problems with right and left RL fractional derivatives. [ 34 , 35 ] Zhang gave the fractional differential equations in terms of combined Riemann–Liouville derivatives. [ 36 ] Wang et al . studied the cyclic integrals and Routh equations of fractional Lagrange system. [ 37 ] However, these fractional derivatives are in integral form, thus it is extremely difficult to work with these definitions. Recently, Khalil et al . introduced a new simple well-behaved definition of the fractional derivative called conformable fractional derivative. [ 38 ] Subsequently, Abdeljawad developed the definitions there and set the basic concepts in this new simple interesting fractional calculus. [ 39 ] The definition and properties of the conformable fractional derivative are coincident with the usual derivative, which is in limit form. In this paper, we use the conformable fractional derivatives to study the fractional non-Noether symmetries of Hamilton systems. We firstly investigate the fractional Hamilton’s canonical equations on the conformable fractional derivative, then, the corresponding fractional non-Noether conserved quantities are presented based on the motion equations.

2. Definitions and properties of conformable fractional derivative and integral

In this section, we present some fundamental definitions and properties of conformable fractional derivative and integral. [ 38 , 39 ] Furthermore, we also study the multivariable differential calculus of conformable fractional derivative, which will be used in the following sections.

2.1. Definition and properties of conformable fractional derivative and integral

Definition 1 Conformable fractional derivative Given a function f : [0, ∞) → R . Then the “conformable fractional derivative” of f of order α is defined by

for all t > 0, α ∈(0, 1). If f is α -differentiable in some (0, a ), a > 0, and lim t →0 + f ( α ) ( t ) exists, then define

We can write f ( α ) ( t ) for T α ( f )( t ) to denote the conformable fractional derivatives of f of order α . In addition, if the conformable fractional derivative of f of order α exists, then we simply say f is α -differentiable.

Theorem 1 Let α ∈ (0, 1] and f , g be α -differentiable at a point t > 0. Then

If f is differentiable, then

Definition 2 Conformable fractional integral

where the integral is the usual Riemann improper integral, and α ∈ (0, 1].

Theorem 2 Let f : ( a , b ) → R be differentiable and 0 < α ≤ 1. Then, for all t > a we have

Definition 3 Chain rule Assume f , g : ( a , ∞) → R be α -differentiable functions, where 0 < α ≤ 1. Let h ( t ) = f ( g ( t )). Then h ( t ) is α -differentiable and for all t with t ≠ a and g ( t ) ≠ 0 we have

Then, we can easily prove the following multivariable differential calculus.

Definition 4 Let x = x ( t ) and y = y ( t ) be differentiable at t , and let z = f ( x , y ) be differentiable at ( x ( t ), y ( t )). Then z = f ( x ( t ), y ( t )) is differentiable at t and

Equation ( 10 ) can be explained by the following formula:

3. The Hamilton principle with conformable fractional derivative

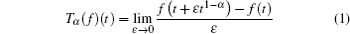
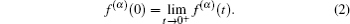
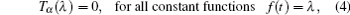
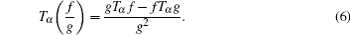
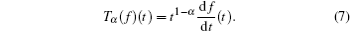
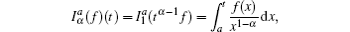
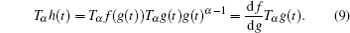
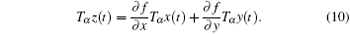
Firstly, let us study the exchanging relationship with respect to the isochronous variation and the fractional derivatives. Considering two infinitely closed orbits: γ and γ + d γ , we denote the generalized coordinates by q = q ( t , γ ) and q ′ = q ( t , γ + d γ ), corresponding to the two infinitely closed orbits individually in giving time, where q = { q 1 , q 2 , …, q n }. We define the isochronous variation as

Extending q ( t , γ + d γ ) to the linear terms of d γ , then we obtain

Substituting Eq. ( 13 ) into Eq. ( 12 ), we have

then we have

Using Eq. ( 12 ), we obtain

Comparing Eqs. ( 15 ) and ( 16 ), we obtain the exchanging relationship

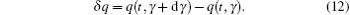
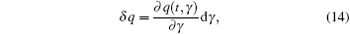
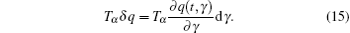
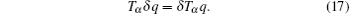
Now we consider a mechanical system of n generalized coordinates q s ( s = 1, 2, …, n ), the Lagrangian of the system is L ( t , q s , T α q s ) ( s = 1, 2, …, n ), and we define the fractional Hamilton action as

where all the variations of the variables are isochronous, and the terminal conditions are given by

Then, the fractional Hamilton principle can be written as

4. Hamilton’s canonical equations with conformable fractional derivative

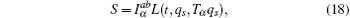
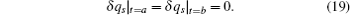
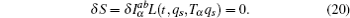
In this section, we study the fractional Hamilton’s canonical equation based on the Hamilton principle. First, let us introduce the generalized momenta as

where the Lagrangian depends on the fractional time derivatives of coordinates in the form L ( t , q s , D α q s ). Then, the Hamiltonian depending on the fractional time derivatives can be expressed as

Substituting Eq. ( 22 ) into Eq. ( 20 ), we have

Then, we obtain

Taking the commutable relation ( 17 ), we have

According to Eq. ( 5 ), we obtain

Substituting Eq. ( 26 ) into Eq. ( 25 ), we derive

From Eq. ( 8 ), we obtain

Using the terminal condition ( 19 ), we obtain

Then, we have

Calculating the derivative of Eq. ( 22 ) with respect to p αs , we acquire

Substituting Eq. ( 31 ) into Eq. ( 30 ) and considering that δq s ( s = 1, 2, …, n ) are independent, we obtain

According to Eq. ( 7 ), we can change Eqs. ( 31 ) and ( 32 ) into the following form:

and

Equations ( 31 ) and ( 32 ), as well as equations ( 33 ) and ( 34 ), are all called Hamilton’s canonical equations with conformable fractional derivative. From Eqs. ( 33 ) and ( 34 ), we can observe that the forms of fractional Hamilton’s canonical equations are in accordance with the usual Hamilton’s canonical equations, which just add the fractional gene t 1− α . The fractional Hamilton’s canonical equations are equivalent to the usual Hamilton’s canonical equations by taking α = 1.

5. Non-Noether conserved quantities with conformable fractional derivative

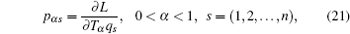
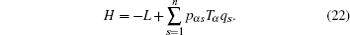
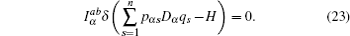
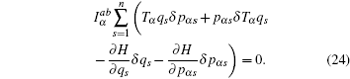
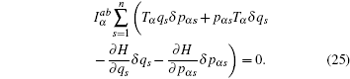
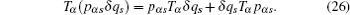
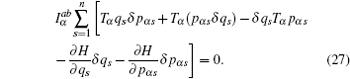
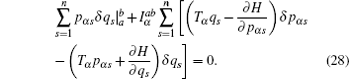
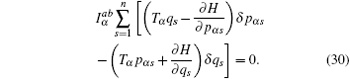
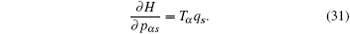
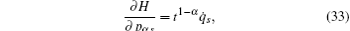
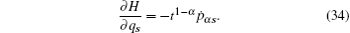
Now we consider a mechanical system of n generalized coordinates q s ( s = 1, 2, …, n ) and n generalized momentums p αs ( s = 1, 2,…, n ), and the Hamilton’s canonical equations are in the form

Equations ( 35 ) and ( 36 ) can be written as

or

Introducing the general infinitesimal transformations

where ε is a small parameter, ε s and η s are the generators of the infinitesimal transformations.

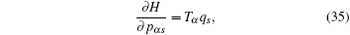
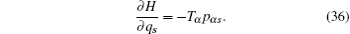
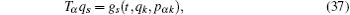
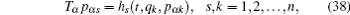
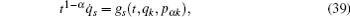
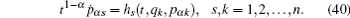
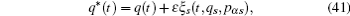
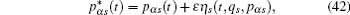
According to the theory of invariance of the differential equations under the infinitesimal transformations, if equations ( 37 ) and ( 38 ) keep invariant under the infinitesimal transformations, then the generators satisfy the following equations:

that is,

where

is the operator of infinitesimal generators, and its extensions

Substituting Eqs. ( 45 ) and ( 46 ) into Eqs. ( 47 ) and ( 48 ), we obtain the following determining equations:

According to Eq. ( 7 ), it can also be written in the following form:

Here we point out that the determining equations with the fractional gene are in accordance with the usual determining equations when taking α = 1. Equations ( 49 )–( 52 ) are applicable to the general case. Then, we have the following theorem.

Theorem 3 For the Hamiltonian system ( 37 ) and ( 38 ), if there exists a gauge function G ( t , q s , p αs ) such that

where ψ is an invariant of the general infinitesimal transformations, then the following quantity can be found:

Proof Firstly, we point out the fact that X (0) ( ψ ) = X (1) ( ψ ) = 0. Then, we demonstrate the theorem by taking α order derivative of ϕ

We have the following easily proven identities ( f ( t , q s , p αs ) is arbitrary):

Using Eqs. ( 56 ), ( 57 ), and ( 60 ), we obtain

According to Eqs. ( 58 ) and ( 59 ), we have

Considering the determining equations ( 51 ) and ( 52 ), we obtain

Comparing Eq. ( 61 ) with Eq. ( 63 ), we derive

From the gauge function ( 53 ), we have

which clarifies the theorem.

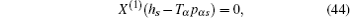
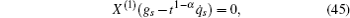
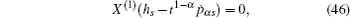
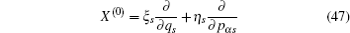
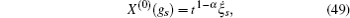
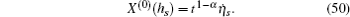
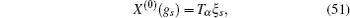
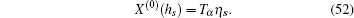
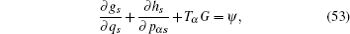
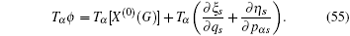
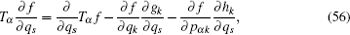
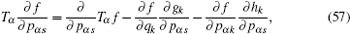
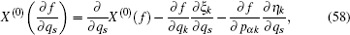
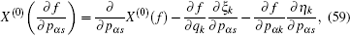
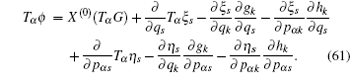
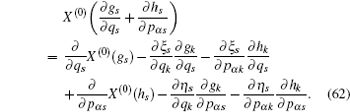
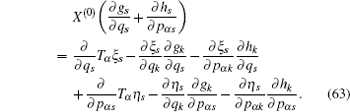
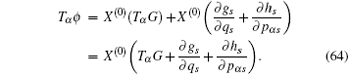
We have shown that the form of conserved quantity with fractional calculus is in accordance with the usual one of the systems. It is common and when we take α = 1, the conserved quantity ( 54 ) is equal to the general case.

6. An illustrated example

Let us consider the following fractional mechanical system, the Lagrangian is

and study its non-Noether conserved quantities. Obviously, we have

The Hamilton function of the system is given by

According to the Hamilton’s canonical equations ( 31 ) and ( 32 ), we obtain

From the determining equations ( 49 ) and ( 50 ), we have

One solution of Eq. ( 77 ) is

where c 1 , c 2 , c 3 , c 4 , c 5 , and c 6 are constants.

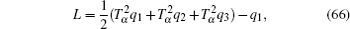
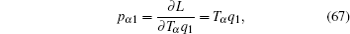
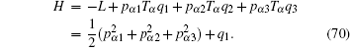
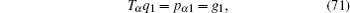
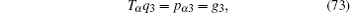
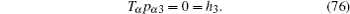
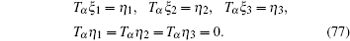
Then, the gauge equation gives

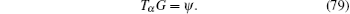
Let ψ = T α ( q 2 p α 3 ) − T α ( q 3 p α 2 ), then X (0) ( ψ ) = X ( 1 ) ( ψ ) = 0, ψ is an invariant.

Therefore, we can find a gauge function

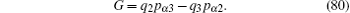
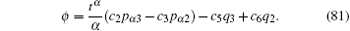
Substituting Eqs. ( 78 ) and ( 80 ) into Eq. ( 54 ), we obtain the following non-Noether conserved quantity:

7. Conclusions

In this paper, we propose a new method to study the complex Hamilton systems with fractional derivatives. The motion equations and non-Noether symmetry theories of fractional Hamilton systems are established by the conformable fractional derivative. The forms of the results are identical to the general ones, and they may change into the general cases when making α = 1. Using this conformable fractional derivative, all the fractional differential equations can be translated into general differential equations and we can easily study the fractional nonholonomic system, the fractional electromechanical coupling system, and the problems of fractional anomalous diffusion.

Reference
1 Noether A E 1918 Math. Phys. KI II 235
2 Li Z P 1981 Acta Phys. Sin. 30 1659 (in Chinese)
3 Mei F X 2000 J. Beijing Inst. Technol. 9 120
4 Mei F X 2001 Chin. Phys. 10 177
5 Hojman S A 1992 J. Phys. A: Math. Gen. 25 L291
6 Gonzaler-Cascon F 1994 J. Phys. A: Math. Gen. 27 L59
7 Lutzky M 1995 J. Phys. A: Math. Gen. 28 L637
8 Mei F X 2002 Chin. Sci. Bull. 47 1544 (in Chinese)
9 Mei F X 2003 Acta Phys. Sin. 52 1048 (in Chinese)
10 Fu J L Chen L Q Xie F P 2004 Chin. Phys. Soc. 13 1611
11 Fang J H Liao Y P Peng Y 2004 Chin. Phys. Soc. 13 1620
12 Zhou S Fu H Fu J L 2011 Sci. Chin. Phys. Mech. Astron. 54 1847
13 Zhang S H Chen B Y Fu J L 2012 Chin. Phys. B 21 100202
14 Zhou Y Zhang Y 2014 Chin. Phys. B 23 124502
15 Sun Y Chen B Y Fu J L 2014 Chin. Phys. B 23 110201
16 Zaslavsky G M 2005 Hamiltonian Chaos and Fractional Dynamics Oxford Oxford University Press
17 Tarasov V E 2010 Fractional Dynamics Beijing Higher Education Press
18 Oldham K B Spanier J 1974 The Fractional Calculus New York Academic Press
19 Podlubny I 1999 Fractional Differential Equations San Diego CA Academic Press
20 Miller K S Ross B 1993 An Introduction to the Fractional Calculus and Fractional Differential Equations New York A Wiley-Interscience Publication
21 Hilf R 2000 Applications of Fractional Calculus in Physics Singapore World Scientific Publishing Company
22 Samko S G Kilbas A A Marichev O I 1993 Fractional Integrals and Derivatives–Theory and Applications Linghorne Gordon and Breach Science Publishers
23 Kilbas A A Srivastava H M Trujillo J J 2006 Theory and Applications of Fractional Differential Equations Amsterdam Elsevier B V
24 Zaslavsky G M 2002 Phys. Rep. 371 461
25 Zaslavsky G M Edelman M A 2004 Physica D 193 128
26 Yang J H 2012 Chin. Phys. Lett. 29 104501
27 Tan C Liang Z S Zhang J Q 2014 Acta Phys. Sin. 63 200502 (in Chinese)
28 Wang F Xie T T Deng C Luo M K 2014 Acta Phys. Sin. 63 160502 (in Chinese)
29 Zhou X W Lin L F Ma H Luo M K 2014 Acta Phys. Sin. 63 160503 (in Chinese)
30 Tu Z Lai L Luo M K 2014 Acta Phys. Sin. 63 120503 (in Chinese)
31 Wang F Q Ma X K 2013 Chin. Phys. B 22 030506
32 Riewe F 1996 Phys. Rev. E 53 1890
33 Riewe F 1997 Phys. Rev. E 55 3581
34 Agrawal O P 2002 J. Math. Anal. Appl. 272 368
35 Agrawal O P 2004 Nonlinear Dyn. 38 323
36 Zhang Y 2012 Chin. Phys. B 21 084502
37 Wang L L Fu J L 2014 Chin. Phys. B 23 124501
38 Khalil R Al Horani M Yousef A Sababheh M 2014 J. Comput. Appl. Math. 264 65
39 Abdeljawad T 2015 J. Comput. Appl. Math. 279 57