Cavity linewidth narrowing with dark-state polaritons

Cite this Article

Lin Gong-Wei, Yang Jie, Niu Yue-Ping, Gong Shang-Qing. Cavity linewidth narrowing with dark-state polaritons. Chinese Physics B , 2016, 25(1): 014201 Copy to clipboard

Permissions

Cavity linewidth narrowing with dark-state polaritons

Lin Gong-Wei ^†,, Yang Jie , Niu Yue-Ping ^‡,, Gong Shang-Qing ^§,

Department of Physics, East China University of Science and Technology, Shanghai 200237, China

† Corresponding author. E-mail: gwlin@ecust.edu.cn

‡ Corresponding author. E-mail: niuyp@ecust.edu.cn

§ Corresponding author. E-mail: sqgong@ecust.edu.cn

Project supported by the National Natural Science Foundation of China (Grants Nos. 11204080, 11274112, 91321101, and 61275215) and the Fundamental Research Fund for the Central Universities of China (Grants No. WM1313003).

Abstract

We present a quantum-theoretical treatment of cavity linewidth narrowing with intracavity electromagnetically induced transparency (EIT). By means of intracavity EIT, the photons in the cavity are in the form of cavity polaritons: bright-state polariton and dark-state polariton. Strong coupling of the bright-state polariton to the excited state induces an effect known as vacuum Rabi splitting, whereas the dark-state polariton decoupled from the excited state induces a narrow cavity transmission window. Our analysis would provide a quantum theory of linewidth narrowing with a quantum field pulse.

PACS : 42.50.Gy ; 42.50.Pq ; 32.80.Qk

Keyword : cavity electromagnetically induced transparency ; linewidth narrowing ; dark-state polariton

Show Figures

1. Introduction

Electromagnetically induced transparency (EIT) is a coherent interference effect where the absorption and dispersion of a resonant medium are strongly modified by a coupling field acting on the linked transition. ^{[ 1 – 4 ]}The EIT medium in an optical cavity known as intracavity EIT was first discussed by Lukin et al. ^{[ 5 ]}They have shown that the cavity response is drastically modified by intracavity EIT, resulting in frequency pulling and a substantial narrowing of spectral features. By following this seminal work, significant experimental advance has been made in narrowing the cavity linewidth ^{[ 6 – 9 ]}and enhancing the cavity lifetime. ^{[ 10 ]}

The previous semi-classical treatments of cavity linewidth narrowing and lifetime enhancing with intracavity EIT were based on the solution of the susceptibility of EIT system. Here we present a quantum-theoretical treatment of cavity linewidth narrowing with intracavity EIT. By means of intracavity EIT, the photons in the cavity are in the form of cavity polaritons: bright-state polariton and dark-state polariton. Strong coupling of the bright-state polariton to the excited state induces an effect known as vacuum Rabi splitting, whereas the dark-state polariton decoupled from the excited state induces a narrow cavity transmission window v = cos ²θ v ₀, with v ₀being the empty-cavity linewidth and θ the mixing angle of the dark-state polariton. ^{[ 11 ]}When the atom-cavity system is in the collective strong coupling regime, a weak control field is sufficient for avoiding the absorption owing to spontaneous emission of the excited state, and then the dark-state polariton induces a very narrow cavity linewidth.

2. Quantum dynamics of intracavity EIT

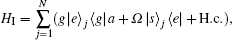
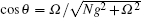
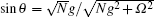
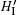
Now we try to solve the quantum dynamics of EIT in an optical standing-wave cavity with input–output processes (Fig. 1(a) ). We consider an ensemble of N atoms with three levels, two ground states | g 〉, | s 〉, and an excited state | e 〉, forming a Λ -configuration system (see Fig. 1(b) ). The two transitions | g 〉 ↔ | e 〉 and | s 〉 ↔ | e 〉 are resonantly coupled by a cavity mode and a laser field, respectively. The interaction Hamiltonian for these coherent processes is described by where a is the annihilation operator of the cavity mode, g ( Ω ) is the coupling strength of quantized cavity mode (laser field) to the corresponding transition. After defining the collective atomic operators with μ = e , s , we rewritten H _Ias ^{[ 12 ]}

where only the coupling constant g between the atoms and the quantized cavity mode is collectively enhanced by a factor

, since we have assumed that all atoms are initially in their ground states, i.e.,

, and the average photon number n inputted into the cavity is so small that almost all atoms are in the ground state | g 〉 at all times. One can define two standing-wave cavity polaritons: ^{[ 13 ]}a dark-state polariton m _D= cos θa − sin θ C _s, and a bright-state polariton m _B= sin θa + cos θ C _s, with

and

. In terms of these cavity polaritons the Hamiltonian

can be represented by

Fig. 1.

(a) Schematic setup to cavity linewidth narrowing with dark-state polaritons. (b) Relevant atomic level structure and transitions.

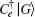
The cavity dark-state polariton is decoupled from the collective excited state

. We note that the dark-state polariton in intracavity Λ -configuration system with optomechanical resonator have been observed in the experiment. ^{[ 13 ]}The dark state polarition is valid when the condition, R = [1 + η ₂+ η ₁( κ / γ _s)] ²Ω ²/( Ng ²) ≫ 1, ^{[ 13 ]}is satisfied, where η ₁= N | g | ²/( κ γ _e) ( η ₂= | Ω | ²/( γ _sγ _e)) is the cooperativity of cavity mode a (ground state | s 〉), with κ , γ _e, and γ _sbeing the decay rate of bare cavity mode a, excited state | e 〉, and the ground state | s 〉, respectively.

The external fields interact with cavity mode a through two input ports α _in, β _in, and two output ports α _out, β _out. The Hamiltonian for the cavity input–output processes is described by ^{[ 14 ]}

where ω is the frequency of the external field, and Θ ( ω ) with the standard relation [ Θ ( ω ), Θ ^†( ω ′)] = δ ( ω − ω ′) denotes the one-dimensional free-space mode. We express the Hamiltonian H _in-outin the polariton bases as

with κ _D= cos ²θ κ and κ _B= sin ²θκ .

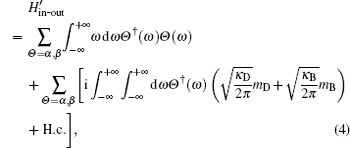
In the intracavity EIT system, only the bright-state polariton m _Bresonantly couples to the excited state, leading to the splitting of the cavity transmission peak for the bright-state polariton m _Binto a pair of resolvable peaks at , ^{[ 15 ]}with ω ₀being the cavity resonant frequency. For the cavity transmission near the cavity resonant frequency ω ₀, the probability P _Bfor excitation of bright-state polariton m _Bscales with 1/(1 + η ₁+ η ₂). ^{[ 13 ]}Under the condition

the probability P _B= 1/[1 + Ng ²/( κγ _e) + Ω ²/( γ _sγ _e)] ≪ 1, thus one can neglect bright-state polariton m _Bto calculate the cavity transmission spectrum near the cavity resonant frequency ω ₀.

According to quantum Langevin equation, the evolution equation of the cavity dark-state polariton m _Dis given by ^{[ 14 ]}

Using the relationships between the input and output modes at each mirror ^{[ 14 ]}

and

and the Fourier transformations

with Λ = m _D, α _in, α _out, β _in, β _out, we can find

where Δ ( ω ) = ω – ω ₀, and we have assumed that the photons enter into the cavity from the input port β _in( α _in= 0). Then the transmission spectrum for intracavity EIT is described by

As depicted in Fig. 2 , the transmission spectrum T can be controlled by the external coherent field. Then the calculation of cavity linewidth v , i.e., the full width at half height of T ( ω ), gives

where ν ₀= 2 κ is the empty-cavity linewidth. ^{[ 14 ]}

	Figure Option View Download New Window
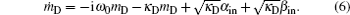
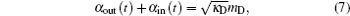
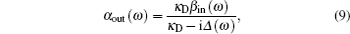
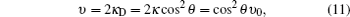
	Fig. 2. Transmission spectrum T as a function of Δ ( ω )/ κ for Ω = {5 g ,0.5 g } on the assumption that N = 400 and g = κ = γ _e.

To obtain the expression of cavity linewidth v in Eq. ( 11 ), we have ignored the bright-state polariton m _Band the atomic spontaneous emission. Next we perform the numerical simulation of the cavity transmission spectrum with the master equation. ^{[ 16 ]}From in Eq. ( 4 ), we see that both the polaritons m _Dand m _Bare coupled to the continuous modes , and thus dissipate in the same way as the bare cavity mode a, with the decay process ^{[ 16 ]}

where ρ is the reduced density operator for the intracavity system. When a weak probe field is applied to the cavity–atom system, the dynamics evolution of the system is governed by the master equation

where

^{[ 17 ]}describes the driving probe fields with the effective amplitude E in natural units and the frequency detuning Δ ( ω ), the last term in Eq. ( 13 ) describes the atomic spontaneous emission from the excited state, and we have ignored the decay of the ground states since γ _s≪ κ , γ _e. We calculate the cavity transmission, which is proportional to the mean intracavity photon number. ^{[ 18 ]}Figure 3 shows the transmission spectrum T versus the normalized frequency detuning Δ ( ω )/ κ , assuming the relevant parameters ( g , κ , γ _e)/2 π ≈ (16,3.8,2.6) MHz, ^{[ 19 ]}

, and

. From Fig. 3 , we see that for cavity EIT system, there are three transmission peaks, i.e., a very narrow middle peak and two very small side peaks. The cavity dark-state polariton m _Dinduces the narrow peak in the middle of transmission spectrum, and the bright-state polariton m _Bresonantly coupled to the excited state leads to the splitting of the cavity transmission peak for itself into a pair of small side peaks at

. ^{[ 15 ]}

	Figure Option View Download New Window
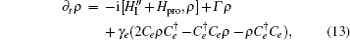
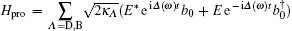
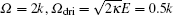
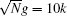
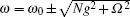
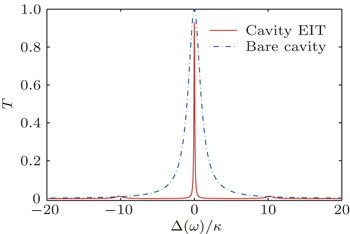	Fig. 3. Transmission spectrum as a function of Δ ( ω )/ κ , with cavity EIT and bare cavity, assuming the relevant parameters ( g , κ , γ _e)/2 π ≈ (16,3.8,2.6) MHz, ^{[ 19 ]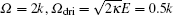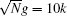}, and .

3. Brief discussion

Now we briefly discuss the results of our theoretical treatment of intracavity EIT. If , the dark-state polariton will induce a very narrow cavity linewidth v = v ₀cos ²θ ≈ v ₀Ω ²/( Ng ²) ≪ v ₀. However, in order that the dark state polarition is valid, we require the condition ^{[ 13 ]}R = [1 + η ₂+ η ₁( κ / γ _s)] ²Ω ²/( Ng ²) ≫ 1. When Ω is very small, R ≈ [ η ₁( κ / γ _s)] ²Ω ²/( Ng ²) ≫ 1, i.e.,

Thanks to the long ground-state coherence with a cold atomic ensemble, ^{[ 20 ]}γ _s≈ 2 π kHz is two order smaller than other parameters g , γ _e, and κ , thus the condition in Eq. ( 14 ) can be easily satisfied. If the atom–cavity system is in the collective strong coupling regime

, even when the control field is so weak that Ω < g , both the required conditions in Eqs. ( 5 ) and ( 14 ) could be satisfied. For example, Ω = 0.1 g < g , g = γ _e= κ = 10 ²γ _s, and N = 100, then both conditions

and

are satisfied. The cavity linewidth v directly links to cavity Q-factor. ^{[ 21 ]}Thus, the cavity linewidth narrowing with quantum field offers a potential approach to enhance the cavity Q-factor and prolong the cavity lifetime of single photons by changing Ω .

4. Conclusion

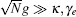
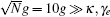
In summary, we have performed a theoretical investigation of intracavity EIT quantum mechanically. In intracavity EIT system, the cavity photons are in the form of cavity polaritons: bright-state polariton and dark-state polariton. Strong coupling of the bright-state polariton to the excited state leads to an effect known as vacuum Rabi splitting, whereas the dark-state polariton decoupled from the excited state induces a narrow transmission window. If the atom–cavity system is in the weak coupling regime, a strong control field is required for avoiding the absorption owing to spontaneous emission of the excited state. However, if atom-cavity system is in the collective strong coupling regime, a weak control field is sufficient for avoiding the absorption, and then the dark-state polariton induces a very narrow cavity linewidth. Our quantumtheoretical treatment of intracavity EIT would provide an alternative theory of linewidth narrowing with quantum field pulses.

Reference

1	Harris S E 1997 Phys. Today 50 36
2	Fleischhauer M Imamoglu A Marangos J P 2005 Rev. Mod. Phys. 77 633
3	Hu Z F Ma Y S Deng J L He H J Wang Y Z 2009 Chin. Phys. B 18 0199
4	Yan X B Gu K H Fu C B Cui C L Wu J H 2014 Chin. Phys. B 23 114201
5	Lukin M D Fleishhauer M Scully M O Velichansky V L 1998 Opt. Lett. 23 295
6	Wang H Goorskey D J Burkett W H Xiao M 2000 Opt. Lett. 25 1732
7	Wu H B Xiao M 2007 Opt. Lett. 32 3122
8	Hernandez G Zhang J P Zhu Y F 2007 Phys. Rev. A 76 053814
9	Wu H B Gea-Banacloche J Xiao M 2008 Phys. Rev. Lett. 100 173602
10	Lauprêtre T Proux C Ghosh R Schwartz S Goldfarb F Bretenaker F 2011 Opt. Lett. 36 1551
11	Fleischhauer M Lukin M D 2000 Phys. Rev. Lett. 84 5094
12	Gorshkov A V André A Fleischhauer M Sørensen A S Lukin M D 2007 Phys. Rev. Lett. 98 123601
13	Dong C H Fiore V Kuzyk M C Wang H L 2012 Science 338 1609
14	Walls D F Milburn G J 1994 Quantum Optics 1nd edn. Berlin Springer-Verlag 121 127
15	Boca A Miller R Birnbaum K M Boozer A D McKeever J Kimble H J 2004 Phys. Rev. Lett. 93 233603
16	Walls D F Milburn G J 1994 Quantum Optics 1nd edn. Berlin Springer-Verlag 96
17	Imamouǧlu A Schmidt H Woods G Deutsch M 1997 Phys. Rev. Lett. 79 1467
18	Kómár P Bennett S D Stannigel K Habraken S J M Rabl P Zoller P Lukin M D 2013 Phys. Rev. A 87 013839
19	Boozer A D Boca A Miller R Northup T E Kimble H J 2007 Phys. Rev. Lett. 98 193601
20	Bao X H Reingruber A Dietrich P Rui J Duck A Strassel T Li L Liu N L Zhao B Pan J W 2012 Nat. Phys. 8 517
21	Grinberg P Bencheikh K Brunstein M Yacomotti M A Dumeige Y Sagnes I Raineri F Bigot L Levenson J A 2012 Phys. Rev. Lett. 109 113903