† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11164014 and 11364025) and Gansu Science and Technology Pillar Program, China (Grant No. 1204GKCA057).
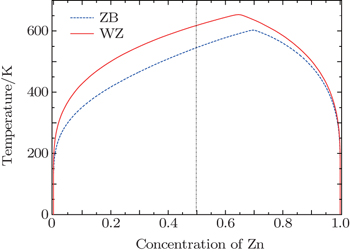
The first-principles calculations based on density functional theory combined with cluster expansion techniques and Monte Carlo (MC) simulations were used to study the phase diagrams of both wurtzite (WZ) and zinc-blende (ZB) Cd 1– x Zn x S alloys. All formation energies are positive for WZ and ZB Cd 1– x Zn x S alloys, which means that the Cd 1– x Zn x S alloys are unstable and have a tendency to phase separation. For WZ and ZB Cd 1– x Zn x S alloys, the consolute temperatures are 655 K and 604 K, respectively, and they both have an asymmetric miscibility gap. We obtained the spatial distributions of Cd and Zn atoms in WZ and ZB Cd 0.5 Zn 0.5 S alloys at different temperatures by MC simulations. We found that both WZ and ZB phases of Cd 0.5 Z n 0.5 S alloy exhibit phase segregation of Cd and Zn atoms at low temperature, which is consistent with the phase diagrams.
Both CdS and ZnS are II–VI direct band gap semiconductors, and their band gaps are 2.40 eV and 3.65 eV, respectively. [ 1 – 3 ] The former is a typical material for the buffer layer of the high-efficiency CuIn 1– x Ga x Se 2 thin film solar cells. [ 4 ] However, cadmium, a kind of heavy metal toxic element, can do harm to the environment and human health. To reduce the cadmium usage as well as to improve the optical and electronic properties of the buffer layer, one feasible way is to replace CdS by Cd 1– x Zn x S solid solution. The band gap and light transmission of CdS can be improved by doping with Zn. [ 5 – 7 ]
To date, the Cd 1– x Zn x S alloys have been widely studied both experimentally and theoretically. In experiments, researchers mainly focused on the methods to synthesize Cd 1– x Zn x S alloys. For example, many methods, such as the chemical co-precipitation method, [ 8 , 9 ] chemical bath deposition (CBD), [ 10 – 13 ] chemical vapor deposition, [ 14 ] molecular beam epitaxy (MBE), [ 15 ] solution growth technique (SGT), [ 16 ] true liquid crystalline templating (TLCT), [ 17 ] precipitate-hydrothermal method, [ 18 , 19 ] and solvothermal route, have been proposed. [ 20 ] In addition, there are also many theoretical studies about the properties of Cd 1– x Zn x S solid solutions. Jiao et al. [ 21 ] studied the structural, electronic, and optical properties of zinc-blende Zn 1– x Cd x S and ZnS 1– y Se y alloys. They predicted that Zn 1– x Cd x S and ZnS 1– y Se y alloys are promising materials for solar cells, photoconductors, and electroluminescent devices due to the materials’ high absorption of solar radiation and photoconductivity in the energy region from visible light to ultraviolet. Wan et al. [ 22 ] calculated the crystal structure and thermal properties of Cd 1– x Zn x S alloys at different temperatures. They found that the lattice parameters decrease with the increase of the Zn concentration. Both the specific heat of constant volume and the coefficient of thermal expansion of Cd 1– x Zn x S increase and saturate as the temperature increases. Wu et al. [ 23 ] studied the band gaps, band edges, and electronic properties of both wurtzite (WZ) and zinc-blende (ZB) Cd 1– x Zn x S solid solutions by using the special quasi-random structures combined with the hybrid density functional theory (DFT) calculations. Lu et al. [ 24 ] obtained the phase diagram of WZ Cd 1– x Zn x S solid solution by using the regular solution model with a Bragg–Williams approximation for the entropy of mixing. The binodal curve was determined by drawing a common tangent line to the Gibbs free energy at a given temperature, and the spinodal curve was determined as the curve whose second derivative of Gibbs free energy with respect to the Zn concentration, ∂ 2 (Δ G )/ ∂x 2 , is zero. In their study, the consolute temperature T c of Cd 1– x Zn x S solid solution is 613 K. The miscibility gap is asymmetric, showing a deviation toward to the higher x side. Recently, Zhou et al. [ 25 ] calculated the phase diagrams of WZ and ZB Cd 1– x Zn x S solid solutions by using first-principles calculations combined with the regular solution model. They found that the consolute temperature T c and the consolute concentration x c are 1278 K and 0.61 for ZB Cd 1– x Zn x S solid solution, and 1017 K and 0.65 for WZ Cd 1– x Zn x S solid solution, respectively. They indicated that the configuration-average method can improve the mixing enthalpy, which explicitly determines the phase stability of the Cd 1– x Zn x S alloys. [ 26 ] The T c of 1017 K is much higher than that of 613 K reported by Lu et al ., [ 24 ] which is almost impossible according to the phase diagrams of CdS and ZnS and the preparation temperature of the experiment, because the temperature is too high. [ 11 , 27 , 28 ]
In this study, we perform first-principles calculations combined with the cluster expansion and Monte Carlo simulations to obtain the phase diagrams of WZ and ZB Cd 1– x Zn x S solid solutions. This method has been successfully used to study the phase equilibrium of many other alloy systems, [ 29 – 33 ] while it has not been used to study the phase stability of Cd 1– x Zn x S solid solutions. In order to analyze the phase separation of Cd 1– x Zn x S systems intuitively, we also present the spatial distributions of Cd and Zn atoms in the two structures of Cd 0.5 Zn 0.5 S alloys.
To study the phase equilibrium and ground-state structures of the Cd 1– x Zn x S alloys, it is necessary to compute the total energies of all possible configurations by placing Cd and Zn atoms on N sites of the Bravais lattice. It is almost impossible to obtain the total energies of all possible configurations exhaustively by first-principles, because the number of possible configurations 2 N is enormous. The cluster expansion (CE) method constructs an Ising-like Hamiltonian for calculating the energies of different atomic configurations. This method has been illustrated in Refs. [ 34 ]–[ 38 ] in detail. For Cd 1– x Zn x S alloys, each configuration is described by a set of “spin” occupation variables σ i at i sites of the lattice, and σ i = +1 or –1 depending on which kind of atoms occupied site i .
The CE parameterizes the configurational energy (per exchangeable cation) as a polynomial in “spin” occupation variables
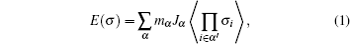
We introduced the cross-validation (CV) score as the criterion to evaluate the predictive power of the cluster expansion. The CV score is defined as

The electronic-structure total-energy calculations of ordered structures, which are required for the construction of the cluster expansion Hamiltonian, were performed using the Vienna ab initio simulation package (VASP). [ 42 , 43 ] The interaction between the core and the valence electrons was included by the frozen-core projector augmented wave (PAW) method. [ 44 , 45 ] The valence electron configurations for the pseudopotentials are Cd: 4d 10 5s 2 , Zn: 3d 10 4s 2 , and S: 3s 2 3p 4 . Both lattice parameters and ionic positions were fully relaxed for all supercells. The plane-wave energy cutoff was 370 eV. The generalized gradient approximation (GGA) functional of Perdew–Burke–Ernzerhof (PBE) was introduced to describe the exchange–correlation energy. [ 46 ] ATAT was used as a script interface to VASP. This script defines a parameter called KPPRA, which automatically sets up the k -point mesh for similar systems. In this work, KPPRA was set to 2000, which for the primitive cells of cubic and hexagonal structures translates to 7×7×7 and 9×9×5 k -point grids, respectively. The convergence tests showed that the increases of energy cutoff and k -points change the total energy by less than 0.01 meV.
We adopted the conventional Monte Carlo simulations to obtain the phase diagrams of the WZ and the ZB Cd 1– x Zn x S alloys as well as the spatial distributions of Cd and Zn atoms in the two structures of Cd 0.5 Zn 0.5 S alloys. We calculated their two-phase equilibrium states. In this paper, we adopted 20×20×20 and 30×30×16 supercells to calculate the phase diagrams for the WZ and the ZB Cd 1– x Zn x S alloys, respectively. The average time for the given precision on the average concentration of the alloy was set to 0.1% in the current simulations. A detailed description of the algorithm underlying this program can be found in Ref. [ 40 ]. The energy of the system was specified by the cluster expansion Hamiltonian. The spatial distributions of Cd and Zn atoms in Cd 1– x Zn x S alloys were also studied. To make the simulation feasible, we kept Cd and Zn atoms fixed at their respective lattice sites and ignore other defects.
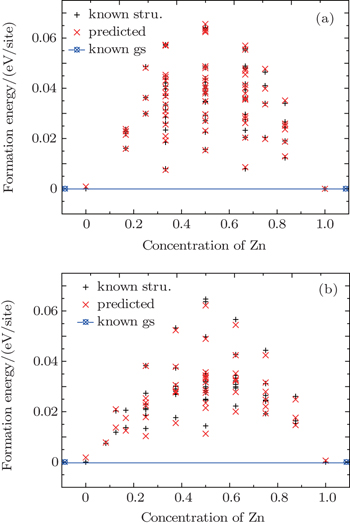
In the cluster expansions of the WZ and the ZB Cd 1– x Zn x S alloys, 68 and 57 input structures have been used, and the CV scores are 1.3 meV and 2.3 meV, respectively. The small CV scores indicate that the predictive ability of the cluster expansions is excellent in this work. The ECIs of the WZ and the ZB Cd 1– x Zn x S alloys obtained from the cluster expansion are given in Table
| Table 1. ECIs of the wurtzite and zinc-blende Cd 1– x Zn x S alloys. . |
As we can see in Table
The formation energies of WZ and ZB Cd 1– x Zn x S solid solutions are shown in Figs.

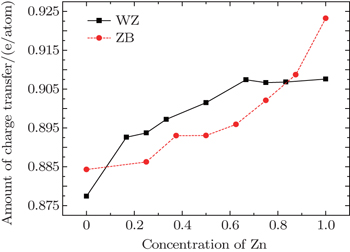
We computed the amount of charge transfer between cations and anions in each input structure of WZ and ZB Cd 1– x Zn x S alloys by Bader charge analysis technique. [ 53 – 55 ] We obtained the average amount of charge transfer to S atoms for each Zn concentration. The statistical error of the average charge transfer was too large for some concentrations with a small number of structures (less than 3), so we did not take them into consideration. As the electrons of Cd and Zn atoms transfer to S atoms in WZ and ZB Cd 1– x Zn x S alloys, the amount of charge gained by S atoms shows the ionicity of these alloys. As we can see in Fig.
Figure
We calculated the spatial distributions of Cd and Zn (active atoms) in WZ and ZB Cd 0.5 Zn 0.5 S alloys at the temperatures of 300 K, 600 K, 650 K, 700 K and 300 K, 550 K, 600 K, 650 K, respectively. As we can see in Fig.
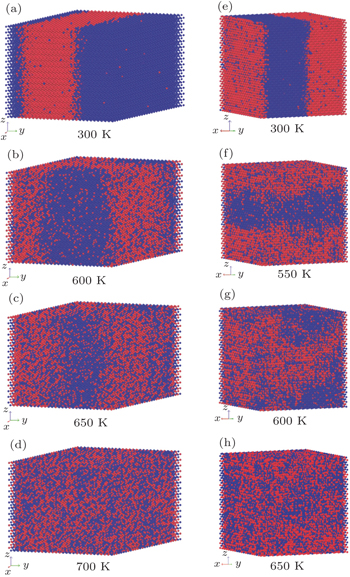 | Fig. 5. Snapshots of (a)–(d) WZ and (e)–(h) ZB Cd 0.5 Zn 0.5 S alloys at different temperatures. Red and blue spheres represent Zn and Cd atoms, respectively. |
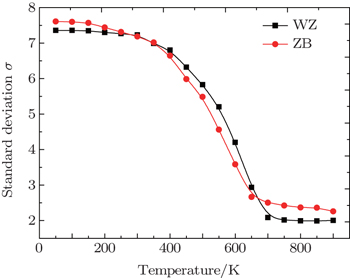
In order to study the spatial distributions of Cd and Zn atoms in WZ and ZB Cd 0.5 Zn 0.5 S alloys at different temperatures quantitatively, we divided the WZ and the ZB supercells into 1800 and 2000 segments, respectively. Each segment has 16 active atoms for both WZ and ZB Cd 0.5 Zn 0.5 S alloys. We counted the number of Cd atoms in each segment. The standard deviation σ was computed as follows:

We obtained the phase diagrams of the wurtzite and the zinc-blende Cd 1– x Zn x S solid solutions by first-principles calculations based on density functional theory combined with the cluster expansion technique and Monte Carlo simulation. For the CdS–ZnS pseudobinary system, all formation energies of WZ and ZB Cd 1– x Zn x S alloys are positive, indicating that both WZ and ZB Cd 1– x Zn x S solid solutions have a tendency to phase separation. The consolute temperatures for the two structures are 655 K and 604 K, respectively, and the miscibility gaps of the two structures are asymmetric, showing a deviation toward to the higher x side. The results of the spatial distributions of Cd and Zn atoms in Cd 0.5 Zn 0.5 S alloys show that the Cd 1– x Zn x S alloys are inhomogeneous and exhibit a phase separation at low temperatures. The analysis of the standard deviations indicates that both WZ and ZB Cd 1– x Zn x S solid solutions have large inhomogeneous degrees below 400 K and rapidly become homogeneous at the temperature range of 400 K to 650 K, and their homogeneous degrees are almost unchanged above 650 K.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 |