Cite this Article
Cheng Jian-Jun, Zhang Hong-Qing. The Wronskian technique for nonlinear evolution equations. Chinese Physics B , 2016, 25(1): 010506  
Permissions
The Wronskian technique for nonlinear evolution equations
Cheng Jian-Jun 1, †, , Zhang Hong-Qing 2
School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, China
Department of Applied Mathematics, Dalian University of Technology, Dalian 116024, China

 

† Corresponding author. E-mail: chengjianjun0355@126.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 51379033, 51522902, 51579040, J1103110, and 11201048).

Abstract
Abstract

The investigation of the exact traveling wave solutions to the nonlinear evolution equations plays an important role in the study of nonlinear physical phenomena. To understand the mechanisms of those physical phenomena, it is necessary to explore their solutions and properties. The Wronskian technique is a powerful tool to construct multi-soliton solutions for many nonlinear evolution equations possessing Hirota bilinear forms. In the process of utilizing the Wronskian technique, the main difficulty lies in the construction of a system of linear differential conditions, which is not unique. In this paper, we give a universal method to construct a system of linear differential conditions.

PACS : 05.45.Yv ; 02.30.Ik ; 02.30.Jr
Keyword : nonlinear evolution equations ; Wronskian determinant ; Young diagram
1. Introduction

Solitons are ubiquitous, appearing in a great variety of contexts, for example, nonlinear optics, plasma physics, fluid dynamics, semiconductors, and many other systems. [ 1 – 3 ] As a matter of fact, the study of such nonlinear waves has attracted extensive attention. Finding exact soliton solutions of integrable nonlinear models is particularly interesting. Based on those exact solutions, we can accurately analyze the properties of propagating soliton pulses in nonlinear physical systems. Towards this goal, many powerful methods for constructing exact solutions of nonlinear evolution equations (NLEEs) have been proposed and developed, which leads to one of the most excited advances in nonlinear science and theoretical physics. These methods include the inverse scattering transformation (IST), [ 4 ] the Bäcklund transformation (BT), [ 5 ] the Darboux transformation (DT), [ 6 ] , the Hirota method, [ 7 – 14 ] and the Wronskian techniques. [ 15 – 27 ] Among these methods, the Wronskian formulations are commonly used for certain NLEEs through the dependent variable transformation.

Soliton solutions can be represented in terms of Wronskian, which can be realized through the Sato theory, [ 28 , 29 ] where τ -functions expressed in terms of Wronskian are governed in common by the Plücker relations. Besides solitons, many other kinds of solutions can also be expressed in terms of Wronskian, such as rational solutions, positons, negatons, complexitons, and mixed solutions. In the process of utilizing the Wronskian technique, the main difficulty lies in the construction of a system of linear differential conditions, which are not unique. Is there any successful and universal tool enabling one to construct a system of linear differential conditions for nonlinear evolution equations possessing Hirota bilinear forms which does not require a deep understanding of mathematics? For this purpose, based on a system of atom equations, we investigate a systematic approach of generalized Wronskian technique to construct a system of linear differential conditions for nonlinear evolution equations.

In this paper, we give a systematic approach to the construction of a system of linear differential conditions. The organization of this paper is as follows. In Section 2, by using atom equations (Plücker-type), we introduce a universal method to construct a system of Wronskian conditions. Some applications will be given in Section 3. Finally, we give the concluding remarks in Section 4.

2. Description of the Wronskian technique

In this section, we introduce the generalized Wronskian technique and a system of atom equations (Plücker-type Young diagram equations), which plays a central role in the construction of generalized Wronskian solutions of nonlinear evolution equations.

Our main tool to tackle the sum is the Wronskian. The Wronskian of a family of functions ϕ 1 , ϕ 2 , …, ϕ N is the determinant of the matrix of their derivatives of order 0 up to N − 1. We use the Wronskian technique in the compact notation introduced by Freeman and Nimmo [ 17 ]

where

The solutions determined by are called the Wronskian determinant solutions.

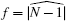
Maya diagrams were first introduced by Sato. [ 28 ] In the language of physics, the diagram for τ represents the vacuum state in which fermions occupy cells 0,1,2,…, N −2, N −1. So the Wronskian is expressed with the vacuum state

There is a one to one correspondence between the Maya diagram and the Young diagram. [ 7 ] Each occupied cell in the Maya diagram corresponds to a vertical line ↑(●) in the Young diagram, and the cell corresponding to the horizontal line →(○) is empty. By using the correspondence between Maya diagrams and Young diagrams, the fourth-order Plücker relation is expressed using Young diagrams as

2.1. Atom equations

Modern science understands the properties of materials by decomposing them into their constituents, or atoms, and has managed to create new materials by combining different atoms. Fundamental soliton equations and their Bäcklund transformation formulae possessing Hirota bilinear forms may be regarded as atom equations for constructing various kinds of Wronskian conditions. The Hirota bilinear forms are governed in common by the fourth or fifth order Plücker-type Young diagram equations (Table 1 ).

Table 1.

The fourth and fifth order Plücker-type Young diagram equations.

.

Lemma 1 When the Wronskian determinant , the Young diagram equations A = 0, B 1 = 0, B 2 = 0 hold.

Proof The fourth and the fifth order Plücker relations are A = 0 and B 1 = 0. We can compute the derivatives of both sides of the fourth Plücker relation A = 0 with respect to variable x as follows:

thus we obtain B 2 = 0.

2.2. Wronskian conditions

Consider a nonlinear evolution equation

where u = u ( x , y , z , t ) is an unknown function and is a polynomial in u = u ( x , y , z , t ) and its partial derivatives, in which the highest order derivatives and nonlinear terms are involved.

Step 1 The following dependent variable transformation

permits us to reduce Eq. ( 5 ) to a Hirota bilinear equation

where a is a constant, ∧ = x n 1 y n 2 z n 3 t m , n = n 1 + n 2 + n 3 + m , the operators D are called Hirota’s operators and are defined by

with X ′ = ( x ′, y ′, z ′).

Step 2 Suppose that ϕ i ( x , y , z , t ), 1 ≤ i ≤ N , has continuous derivatives up to any order, and satisfies the following linear differential conditions:

then

Step 3 Substituting Eq. ( 9 ) into Eq. ( 7 ), collecting together all terms with the same order of operators D , and equating each coefficient of the resulting polynomial (order ≠ 4,5) to zero yields a set of algebraic equations for k j , l j , r j . Then equation ( 7 ) becomes

where

Step 4 Suppose that the Hirota bilinear forms are governed in common by the fourth or fifth order Plücker-type Young diagram equations (Table 1 ).

Case 1 If the Hirota bilinear forms are

from Step 3, we obtain

Case 2 If the Hirota bilinear forms are

where . Then back to Step 3, collecting together all terms with the same order of operators D and equating each coefficient of the resulting polynomial (order ≠ 4 and not including D 2 and D 4 ) to zero yield a set of algebraic equations for k j , l j , r j . We obtain

Case 3 If the Hirota bilinear forms are

where . Then back to Step 3, collecting together all terms with the same order of operators D and equating each coefficient of the resulting polynomial (order ≠ 4,5 and not including D 3 ) to zero yields a set of algebraic equations for k j , l j , r j . We obtain

Case 4 If the Hirota bilinear forms are

where . Then back to Step 3, collecting together all terms with the same order of operators D and equating each coefficient of the resulting polynomial (order ≠ 4,5 and not including D 4 ) to zero yields a set of algebraic equations for k j , l j , r j . We obtain

Case 5 If the Hirota bilinear forms are

where . Then back to Step 3, collecting together all terms with the same order of operators D and equating each coefficient of the resulting polynomial (order ≠ 4,5 and not including D 5 ) to zero yields a set of algebraic equations for k j , l j , r j . We obtain α , β , γ , ξ , η , μ satisfying Eq. ( 13 ).

Step 5 Solving Case 1 to Case 5 and substituting it into Eq. ( 8 ), we can obtain ϕ i satisfying the linear differential conditions (called the Wronskian conditions). If Cases 1 to 5 have no solution, then equation ( 7 ) does not have a Wronskian determinant solution (based on the fourth or fifth order Plücker-type Young diagram equations).

Step 6 By solving the Wronskian conditions, we obtain the Wronskian determinant solutions

3. Applications
3.1. Kadomtsev–Petviashvili equation

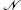
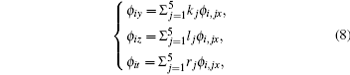
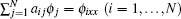
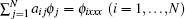
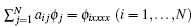
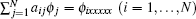
The Kadomtsev–Petviashvili (KP) equation [ 7 ] reads

Under the variable transformation t → −4 t , , it becomes

Notice that equation ( 18 ) has the Hirota bilinear equation

under the Cole Hopf transformation u = 2(ln f ) xx . The KdV equation is a 1+1-dimensional equation describing shallow water waves. The KP equation was introduced to discuss the stability of these waves to perpendicular horizontal perturbations. [ 30 ]

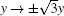
Sato [ 28 ] first discovered that the KP equation is the most fundamental among the many soliton equations. Sato discovered that the polynomial solutions of the bilinear KP equation are equivalent to the characteristic polynomials of the general linear group. Later, he found that the KP equation is equivalent to the motion of a point in a Grassmanian manifold and its bilinear equation is nothing but a Plücker relation. Also, Satsuma had discovered before Sato that the soliton solutions of the KdV equation could be expressed in terms of wronskian determinants. Later, in 1983, Freeman and Nimmo [ 17 ] found that the KP bilinear equation could be rewritten as a determinantal identity if one expresses its soliton solutions in terms of wronskians.

In Refs. [ 7 ] and [ 17 ], the N -soltion solution to Eq. ( 19 ) is expressed in terms of Wronskian. When ϕ i satisfies the following linear differential equations (called the Wronskian conditions):

then the Wronskian determinant τ defined by Eq. ( 1 ) is the solution of Eq. ( 19 ).

In this section, based on the universal method in Subsection 2.2, we give three generalized Wronskian conditions as follows.

Theorem 1 If ϕ i ( x , y , t ), 1 ≤ i ≤ N , has continuous derivatives up to any order, and satisfies the following linear differential conditions:

then the Wronskian determinant f defined by Eq. ( 1 ) is the solution of Eq. ( 19 ).

These new Wronskian conditions (21) are more general than each of the (20) conditions, since we find that any function ϕ i , which can solve one of the (20) conditions satisfies (21) conditions, but the reverse is not true. The Wronskian conditions (22) and (23) are new Wronskian conditions.

From the Wronskian condition (21),

is called the N -Wronskian solution of Eq. ( 19 ), where

and c i ,1 , c i ,2 , l , p i , q i , ξ i 0 , η i 0 are arbitrary constants. So the N -Wronskian solution

is called the N -soliton solution, where (–1) i c i ,1 c i ,2 < 0, i = 1,2,…, N .

Based on the soliton solutions, we plot figures to describe the propagation of the soliton waves. Figure 1 shows one soliton splitting into two solitons given by expression ( 26 ). Figure 2 shows one soliton splitting into two solitons at y = 0 and x = 0 given by expression ( 26 ).

3.2. B-type Kadomtsev–Petviashvili equation

The B-type Kadomtsev–Petviashvili (BKP) [ 31 , 32 ] equation reads

Notice that equation ( 27 ) has the Hirota bilinear equation

under the Cole Hopf transformation u = 2(ln f ) xx . When specialized to t = x , this reduces to the model equation for the shallow water wave. [ 31 ]

The BKP hierarchy (KP hierarchy of B-type) was introduced by Date, Jimbo, Kashiwara, and Miwa [ 33 , 34 ] in 1981. In 2003, Chen et al . [ 35 ] constructed the symmetries and algebraic structures for isospectral and nonisospectral BKP systems associated with the linear problem of Sato theory. The Pfaffian solutions to the BKP equation were presented by Hirota. [ 7 ] However, to the best of our knowledge, the Wronskian solutions to the BKP equation have not been given, and in Ref. [ 36 ], authors thought that the BKP equation only has Pfaffian solutions.

In this section, based on the universal method in Subsection 2.2, we give generalized Wronskian conditions.

Theorem 2 If ϕ i ( x , y , t ), 1 ≤ i ≤ N , has continuous derivatives up to any order, and satisfies the following linear differential conditions:

then the Wronskian determinant f defined by Eq. ( 1 ) is the solution of Eq. ( 28 ).

The isospectral BKP equation is the second member on the BKP hierarchy. In Ref. [ 37 ], based on the universal method in Subsection 2.2, we give three generalized Wronskian conditions.

Fig. 1. One soliton splitting into two solitons expressed by Eq. ( 26 ) with c 1,1 = 1, c 1,2 = 2, c 2,1 = 1, c 2,2 = –2, l = 2, p 1 = p 2 = 1, q 1 = 2, q 2 = 3, ξ 10 = ξ 20 = 1, η 10 = η 20 = 2: (a) t = –1, (b) t = 0, (c) t = 0.5, (d) t = 1.
Fig. 2. One soliton splitting into two solitons at (a) y = 0 and (b) x = 0 given by Eq. ( 26 ) with c 1,1 = 1, c 1,2 = 2, c 2,1 = 1, c 2,2 =−2, l = 2, p 1 = p 2 = 1, q 1 = 2, q 2 = 3, ξ 10 = ξ 20 = 1, and η 10 = η 20 = 2.
4. Conclusion

The Wronskian technique is a powerful tool to construct multi-soliton solutions for many nonlinear evolution equations possessing Hirota bilinear forms. In the process of utilizing the Wronskian technique, the main difficulty lies in the construction of a system of linear differential conditions, which is not unique. In this paper, we give a universal method to construct a system of linear differential conditions. Based on the method, we establish three generalized linear differential conditions of Wronskian solutions for the Kadomtsev–Petviashvili equation. We also establish the generalized linear differential conditions of Wronskian solutions for the B-type Kadomtsev–Petviashvili and isospectral B-type Kadomtsev–Petviashvili equations. We show that the Wronskian technique together with the Hirota method is sufficient to seek the exact solutions of nonlinear evolution equations in mathematics physics. Similar to many other systematical works on Wronskian solutions, [ 19 , 21 ] the complexiton solutions to KP, BKP, and IBKP equations can also be considered.

Generally speaking, the KP hierarchy only has Wronskian determinant solutions, and the BKP hierarchy only has Pfaffian solutions, but we have established Wronskian solutions for the BKP equation (the first member on the BKP hierarchy) and the IBKP equation (the second member on the BKP hierarchy). So the BKP and IBKP equations have not only Pfaffian solutions but also Wronskian determinant solutions. This property is completely different from that of the KP equation, which only has Wronskian determinant solutions.

It is known that some other solving methods, such as the G ′/ G -expansion method [ 38 ] and the exp-function method, [ 39 ] in principle, can generate all kinds of elementary function solutions, including soliton solutions. Hence it is interesting to explore the relation between the solutions obtained by the Wronskian technique and by other methods. We hope that more new exact solutions to nonlinear evolution equations can be obtained by using the Wronskian technique.

Reference
1 Colin T 1993 Phys. D 64 215
2 Hong W P 2007 Phys. Lett. A 361 520
3 Sun W R Tian B Jiang Y Zhen H L 2014 Annals of Physics 343 215
4 Ablowitz M J Segur H 1981 SIAM, Philadelphia
5 Rogers C Shadwick W R 1982 Bäcklund Transformation and Their Application New York Academic Press
6 Matveev V B Salle M A 1991 Darboux Transformations and Solitons Berlin Springer
7 Hirota R 2004 The Direct Method in Soliton Theory Cambridge Cambridge University Press
8 Hirota R 1971 Phys. Rev. Lett. 27 1192
9 Jarmo H 1987 J. Math. Phys. 28 1732
10 Jarmo H 1987 J. Math. Phys. 28 2094
11 Jarmo H 1987 J. Math. Phys. 28 2586
12 Jarmo H 1988 J. Math. Phys. 29 628
13 Hu X B Wu Y T Geng X G 1999 J. Math. Phys. 40 4180
14 Shen H F Tu M H 2011 J. Math. Phys. 52 032704
15 Chiu S C Ladik J F 1977 J. Math. Phys. 18 690
16 Case K M Chiu S C 1977 J. Math. Phys. 18 2044
17 Freeman N C Nimmo J J C 1983 Phys. Lett. A 95 1
18 Hirota R Tang 1986 J. Phys. Soc. Jpn. 55 2137
19 Ma W X 2002 Phys. Lett. A 301 35
20 Gulmaro C C 2004 J. Math. Phys. 45 4282
21 Ma W X 2005 Nonl. Anal. 63 2461
22 Yan Z 2007 Chaos Solitons Fract. 33 951
23 Sun Y Tam H 2008 J. Math. Anal. Appl. 343 810
24 Zhang D J Zhao S L Sun Y Y Zhou J 2014 Reviews in Mathematical Physics 26 1430006
25 Xu T Tian B 2010 J. Math. Phys. 51 033504
26 Wu J P 2011 Chin. Phys. Lett. 28 050501
27 Pierre G 2013 J. Math. Phys. 54 013504
28 Sato M 1981 Publication of RIMS, Kyoto Univ. 439 30
29 Ohta Y Satsuma J Takahashi D Tokihiro T 1988 Prog. Theor. Phys. Suppl. 94 210
30 Kadomtsev B B Petviashvili V I 1970 Sov. Phys. Doklady. 15 539
31 Jimbo M Miwa T 1983 Res. I. Math. Sci. 19 943
32 Hirota R 1989 J. Phys. Soc. Jpn. 58 2285
33 Date E Jimbo M Kashiwara M Miwa T 1981 Phys. D 82 343
34 Tokunaga T Kadomatsu H Fujiwara H 1981 J. Phys. Soc. Jpn 50 3183
35 Chen D Y Xin H W Zhang D J 2003 Chaos Soliton. Fract. 15 761
36 Tang Y N Ma W X Xu W 2012 Chin. Phys. B 21 070212
37 Cheng J J Wang Z Zhang H Q 2014 J. Nonl. Math. Phys. 21 17
38 Zayed E M E Gepreel K A 2008 J. Math. Phys. 50 013502
39 Bekir A Boz A 2008 Phys. Lett. A 372 1619