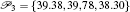† Corresponding author. E-mail:
We present the generalized forms of Parrondo’s paradox existing in fractional-order nonlinear systems. The generalization is implemented by applying a parameter switching (PS) algorithm to the corresponding initial value problems associated with the fractional-order nonlinear systems. The PS algorithm switches a system parameter within a specific set of N ≥ 2 values when solving the system with some numerical integration method. It is proven that any attractor of the concerned system can be approximated numerically. By replacing the words “winning” and “loosing” in the classical Parrondo’s paradox with “order” and “chaos", respectively, the PS algorithm leads to the generalized Parrondo’s paradox: chaos 1 + chaos 2 + ··· + chaos N = order and order 1 + order 2 + ··· + order N = chaos. Finally, the concept is well demonstrated with the results based on the fractional-order Chen system.
Discovered in 1996 and named after the Spanish physicist Parrondo, Parrondo’s paradox states that setting up two losing games together can result in a winning scenario. [ 1 , 2 ] It means that, by alternating two losing strategies in a deterministic way, a positive game can be obtained. Symbolically, we thus have “losing + losing = winning”. For example, in a chess game, the sacrifice of some chess pieces can lead to winning a game; in the stock market, Parrondo’s game offers a possibility to make a profit by investing in losing stocks.
Though it looks contradictory and not every scientist agrees with its principle, [ 3 ] Parrondo’s paradox has still received a lot of attention and become an active topic in many research areas, such as minimal Brownian ratchet, [ 4 ] discrete-time ratchets, [ 5 ] game theory, [ 6 ] and molecular transport, [ 7 ] to name a few.
In receipt of the 1998 Steele Prize for Seminal Contributions to Research, Zeilberger responded that “... combining different and sometimes opposite approaches and viewpoints will lead to revolutions. So the moral is: Don’t look down on any activity as inferior, because two ugly parents can have beautiful children,...”. Indeed, we have witnessed a large number of research works showing the alternations of losing–winning, weakness–strength, order–chaos, and so on, in mathematical systems, control systems, quantum systems, biological systems, and physical systems. These counterintuitive results seem to be typical, not only in computational experiments but also in nature, where the underlying system dynamics are characterized by parameter switching either in an accidental or an intentional way. A review of Parrondo’s paradox can be found in Ref. [ 8 ] and the issues about Parrondo’s paradox were recently investigated in Ref. [ 9 ].
In Ref. [ 10 ], it was proven that Parrondo’s paradox can be generalized, for which a “winning” or “losing” result is obtained by combining N > 2 “losing” or (and) “winning” strategies. The generalization was modeled and demonstrated by applying a parameter switching (PS) algorithm onto nonlinear ordinary differential equations, [ 10 – 12 ] logistic map, [ 13 ] and fractals. [ 14 ]
In this paper, we adopt the PS algorithm to fractional-order differential equations (FDEs), aiming to extend the generalized Parrondo’s paradox to this interesting class of nonlinear systems. Recently, the fractional-order systems have received a lot of attention due to the fact that they are more accurate in modeling many practical systems (see Refs. [ 15 ]–[ 17 ]). Being a counterpart of the integer-order systems, the fractional-order systems are rich in complex dynamics, such as bifurcations, chaos, hyperchaos, etc. [ 18 – 21 ] The control and synchronization issues of these systems have also been studied. [ 18 – 20 , 22 ] To deal with the associated FDEs, different versions of fractional derivatives, such as Grunwald–Letnikov fractional derivative, Reimann–Liouville fractional derivative, and Caputo fractional derivative, [ 23 ] are possible. Since analytical solutions of nonlinear FDEs are usually not obtainable, the use of the numerical integration method such as the Adams–Basforth–Moulton predictor-corrector scheme (ABM) [ 24 ] is common. It is also possible to have a physical realization of the FDE which is mainly based on the frequency domain approximation. [ 25 ] This method has been widely applied, [ 19 , 21 ] yet there are still many arguments about the approximation. [ 26 ]
The rest of this paper is organized as follows. Section 2 describes the PS algorithm for FDEs. Section 3 presents the implementation of the PS algorithm for modeling the generalization of Parrondo’s game. The results are demonstrated with an example of fractional-order Chen’s system, in which Parrondo’s paradox generalization is considered. Finally, the conclusion section closes the paper.
Let us consider the following Caputo-type autonomous initial value problem (IVP)
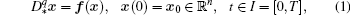
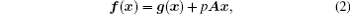
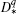

In order to integrate numerically IVP (
Given a set of parameters, 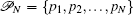

Given N , 

For example, the scheme [2 p 1 , 1 p 2 ] with a fixed h means that the IVP (
By applying expression (
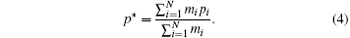
The convergence of the switched solution to the averaged solution under the PS algorithm for the integer-order systems can be proved with the average theorem [ 10 ] or based on the convergence of the used numerical method. [ 11 ] Numerically, the convergence can also be determined by characteristic tools for dynamical systems, such as checking the match between the two trajectories (switched and averaged) in phase plots, time series, Poincaré sections, etc, as for the fractional-order Chen system considered in this paper.
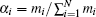
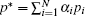
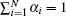
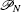
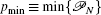
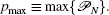
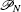
The applications of the PS algorithm are wide. For example, it is possible to obtain the numerical approximation of some attractors of a system modeled by the IVP ( 
Let us consider a system modeled by IVP ( 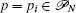
Now, the following notations for the numerically approximated attractors are defined (after neglecting first transients):
• A
• A * is the “switched attractor” obtained by the PS algorithm;
• A p * is the “averaged attractor” obtained from IVP (
If in the known form of Parrondo’s paradox “losing + losing = winning”, we denote chaos := losing and order := winning, one obtains chaos + chaos = order. If one considers the system ( 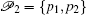
| Table 1. Possible results with PS algorithm for N = 2. . |
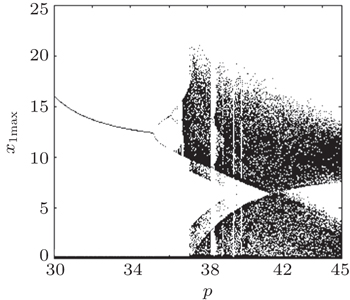
It is interesting to point out that specific attractor, either stable or chaotic, can be obtained with Parrondo’s paradox, despite the original behaviors corresponding to 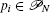
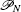
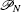
When one considers a general case of N ≥ 2, the following property is held, stating the existence of the generalized Parrondo’s paradox.
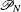
(i) If p * corresponds to a stable periodic motion, and is intercalated by some values of p i belonging to some chaotic windows, then the following generalized Parrondo’s paradox exists:
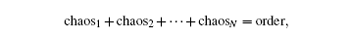
(ii) If p * corresponds to a chaotic motion, and is intercalated by some values p i belonging to some periodic windows, then the following generalized Parrondo’s paradox exists:

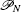
In the following, we focus on the incommensurate fractional-order Chen system, [ 32 ] which can be expressed as
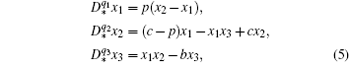
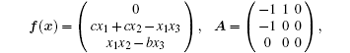
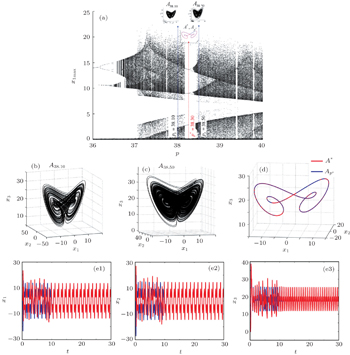
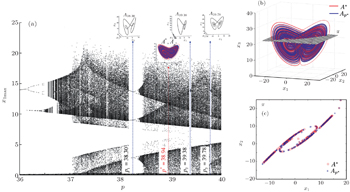
We consider cases which model Parrondo’s variants, i.e., the chaos-control-like and chaos-anticontrol-like actions (the second and the fifth cases in Table
In order to illustrate the match of the switched solution to the averaged solution, we overplot the underlying attractors in the phase space after ignoring the first transients. The matching between the two attractors shows the correctness of the results.
Let us first consider the stable cycle corresponding to p * = 38.30. The periodic cycle can be approximated with the PS algorithm, for example, using [ m 1 p 1 , m 2 p 2 ] with 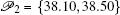
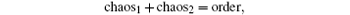
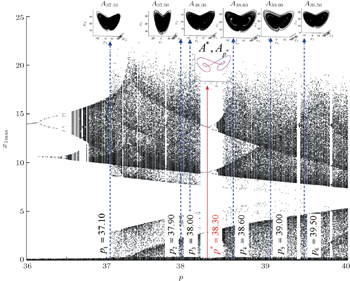 | Fig. 3. Generalized Parrondo’s paradox (chaos control-like): chaos 1 + … + chaos 6 = order, modeled by the PS algorithm under the scheme [2 p 1 ,3 p 2 ,1 p 3 ,2 p 4 ,3 p 5 ,1 p 6 ], with 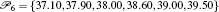 |
It should be emphasized that, the scheme for approximating an attractor is not unique, many different alternatives are possible with the PS algorithm (see Remark 2 (i)). For example, the same stable cycle in the previous example can be obtained by the scheme [2 p 1 , 3 p 2 , 1 p 3 , 2 p 4 , 3 p 5 , 1 p 6 ] with 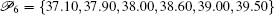
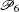

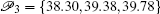

The PS algorithm can be successfully numerically applied in many systems of fractional-order continuous or piecewise continuous (see the case of the new piecewise linear Chen system of fractional-order [ 12 ] ).
We have shown via the PS algorithm that Parrondo’s paradox and its generalizations occur in fractional-order systems. By having N ≥ 2 bifurcation parameters, the PS algorithm leads to the generalized variant of Parrondo’s game: chaos 1 + chaos 2 + … + chaos N = order, which can be considered as a chaos-control-like. Another form of generalized Parrondo’s paradox is order 1 + order 2 + … + order N = chaos, which can be considered as a chaos-anticontrol-like. The simplicity of the PS algorithm resides in the linear dependence on p as given in the term p
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |